
ЛекцииОНИРыбалко А
.docx
|
Рекомендации по работе с научной и технической литературой. Подготовка отчета о НИР. Научный работник, прорабатывающий тему, накапливает большое количество различной информации. Так, библиография кандидатской диссертации насчитывает обычно около 150 наименований. Это значит, что проработать необходимо в 2-3 раза больше источников. Для эффективного анализа этой информации необходимо знать методы ее учета, проработки и анализа. Учет проработанной информации сводится к составлению библиографии. Библиография – это перечень различных информационных документов с указанием следующих данных: фамилия и инициалы автора, наименование источника, место издания, издательство, год издания, объем в страницах. Библиографическое описание нужно приводить в соответствии с действующими стандартами по библиографическому и издательскому делу. Этого требует ДСТУ 3008-95. Проще всего заполнять так, как записано в самом издании, если оно не очень старое. Библиографический перечень удобнее всего составлять на отдельных карточках. Это облегчит работу в дальнейшем, когда надо будет располагать источники либо в алфавитном порядке, либо по разделам работы, либо в порядке упоминания в работе и т.д. Проработка информации сводится к ее изучению и запоминанию. Первым условием эффективной проработки документа является установка, т.е. цель чтения, направленность. Изучение научно-технической информации требует творческого подхода, для чего необходимовдохновение. Но даже если его нет нужно усилием воли заставить себя работать творчески. Иногда с первого раза кажется, что все непонятно, что данная информация слишком сложна. В этом случае нужно заставить себя читать еще и еще. Иногда полезно на время оставить этот документ и заняться другим и вернуться через неделю-две. Внимание и сосредоточенность во многом определяют качество проработки информации. В процессе чтения действуют различные раздражители – музыка, шум, разговоры, собственные мысли и др. Они независимо от человека действуют на центральную нервную систему, ухудшают условия мышления, вызывают утомление. Поэтому, чтобы повысить работоспособность умственного труда, различные помехи следует устранять. Нельзя вдаваться в крайности. Как показывают психологические опыты, работа в полной изоляции от внешней среды также не оптимальна. В качестве помехи в таких случаях выступают собственные мысли, отвлечения. Здесь каждый должен найти свой оптимум. Самостоятельность труда. Каждая страница должна быть неторопливо проанализирована, обдумана примеряна к поставленной цели. Настойчивость и систематичность. Часто, особенно при чтении сложного нового текста четко осмыслить его с первого раза невозможно. Приходится читать и перечитывать, добиваясь полного понимания материала. Систематическое, усидчивое чтение по плану, с обдумыванием и анализом прочитанного намного производительнее бессистемного. Производительность проработки информации существенно зависит от умственной работоспособности. Последняя зависит от умения правильно распределить свою работу во времени, умело использовать перерывы. После 1-2 часов работы нужно делать перерывы на 5-7 минут, физические упражнения, обтирания тела и лица теплой водой или усиленное глубокое дыхание. Прорабатывая текст, необходимо добиваться, чтобы все было понятно. В отдельных случаях нужно не только понять, но и запомнить текст на тот или другой период. Каждый научный работник должен владеть искусством запоминания. Существуют различные способы запоминания. Механический – основан на многократном повторении и заучивании прочитанного («зазубривание»). В этом случае отсутствует логическая связь между отдельными элементами. Этот способ наименее эффективен, он применим в ограниченных случаях: даты, формулы, иностранные слова и др. Доказано, что тренировка памяти многочисленными повторениями малоэффективна. Смысловой способ запоминания основан на запоминании логических связей между отдельными элементами. При чтении необходимо понять не отдельные элементы, а весь текст в целом, его смысл, направленность, значение. Часто достаточно прочесть текст один раз, чтобы его запомнить. Текст хранится в памяти определенное время. Со временем он начинает забываться. Сначала процесс забывания протекает наиболее быстро, со временем темп замедляется. Так, в среднем через один день теряется около 20-25% заученного, через 5 дней – около 35%, через 10 дней – 40%. Повторение – один из эффективных способов запоминания. Повторение бывает пассивным(перечитывание несколько раз) и активным (перечитывание с пересказом). Второй способ сочетает заучивание с самоконтролем, поэтому, он более эффективен. Учитывая характер забывания, материал лучше всего повторить в день чтения или же на следующий день, а затем повторять только периодически и лишь то, что представляет наибольший интерес. Небольшой по объему текст лучше повторить полностью. Большие тексты вначале осваивают в целом, затем повторяют особо трудные фрагменты. Неотъемлемым требованием проработки научно-технической информации является запись прочитанного. Она позволяет лучше его понять, удлинить процесс восприятия информации, лучше запомнить, восстановить в памяти забытое, развить мышление, проанализировать текст, отобрать наиболее важные фрагменты для разрабатываемой темы. Однако запись требует дополнительного времени, которого часто не хватает. Поэтому делать ее нужно правильно. Очень коротко – теряете информацию. Излишне подробно – свидетельство неумения понять и отразить главное. Прорабатывая научно-техническую информацию, применяют выпимки, аннотации, конспекты. Выписка – краткое (или полное) содержание отдельных разделов, глав, страниц информации. Ценность выписок очень высока. Они могут заменить сплошное конспектирование текста, их краткость позволяет в малом объеме накопить большую информацию. Аннотация – это краткая характеристика текста с точки зрения содержания, назначения, формы и др. Аннотации составляют на данный документ информации в целом. Аннотации удобно накапливать на отдельных карточках по разным вопросам прорабатываемой темы. Аннотации позволяют быстро восстановить в памяти текст. Конспект – это подробное изложение содержания информации. Главное в составлении конспекта – это уметь выделить рациональное зерно применительно к разрабатываемой теме. Конспект должен быть содержательным, полным и по возможности кратким. Полнота здесь означает не объем, а все то, что является главным в данной информации. Правило: чтобы конспект был кратким, его нужно составлять своими словами, что требует осмысливания, анализа прочитанного. Рекомендуется применять сокращенные слова, но так, чтобы не потерять смысл. В сокращенном тексте следует сохранить все знаки препинания. Полезно каждому научному работнику иметь свой словарь сокращенных слов. Конспект должен быть правильно оформлен. Каждое произведение желательно конспектировать в отдельной тетради. Запись вести только с одной стороны листа с полями около ¼ ширины листа. Текст нужно разбивать на абзацы и иерархические пункты, например, 1.1.1, 1.1.2, 1.1.3, …, 1.2.1, 1.2.2 … Для выделения главных мыслей нужно применять подчеркивание сплошной, волнистой, пунктирной и т.п. линиями. Иногда конспект нужно пополнять новыми материалами, своими мыслями, анализом и т.д. По тексту ставят номера, которыми отмечают соответствующие дополнения на полях или обратной стороне листа. Существуют два способа составления конспектов. Первый – подобранная информация по теме прорабатывается последовательно. Вначале составляют конспект на каждую информацию, а затем все объединяют в одно обзорное произведение. Этот способ наиболее распространен, но он не достаточно эффективен, т.к. требует большой затраты времени. Второй способ, выборочный, заключается в следующем. Подобранную информацию располагают в ряд по степени полноты, актуальности, новизны. Вначале изучают самую полную современную информацию высокого научного уровня. С помощью оглавления составляют полный план темы. Далее приступают к беглой проработке менее важной, второстепенной, информации, дополняя ею план основного первоисточника. В случае повторения второстепенную информацию опускают. Второй способ сокращает время на подготовку обобщенного конспекта. Подготовка отчета о НИР Все материалы, полученные в процессе исследований, систематизируют и оформляют в виде научного отчета. К отчету предъявляются такие основные требования:
При составлении отчета следует руководствоваться требованиями ДСТУ 3008-95. Документация. Отчеты в сфере науки и техники. Структура и правила оформления. 2 ТРЕБОВАНИЯ К ПОРЯДКУ ИЗЛОЖЕНИЯ МАТЕРИАЛА ОТЧЕТА 2.1 Структура отчета 2.1.1 Отчет условно разделяют на:
2.1.2 Структурная схема отчета приведена на рисунке 1. 2.2 Вводная часть 2.2.1 Вводная часть содержит следующие структурные элементы:
2.2.3 Требования к структурным элементам вводной части ….. 2.3. Основная часть 2.3.1 ….. 2.3.2 ….. 2.4 Приложения 2.5 Материалы в конце отчета 2.5.1 Материалы в конце отчета включают в себя структурный элемент «Обложка» . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Рисунок 1 – Структурная схема отчета |
|
Лекция №6. Методы математической статистики |
|
Тема. Задачи математической статистики и первичная обработка данных 6.1 Задачи математической статистики При изложении основ теории вероятностей, о вероятностях случайных событий и о распределениях случайных величин говорилось как о чем-то заранее известном. Так в испытаниях Бернулли считалась заданной вероятность появления события в одном испытании, а в определении попадания случайной величины в заданный интервал плотность вероятности считалась также заданной. На практике обычно такой информацией не располагают, все необходимые вероятностные характеристики случайных событий и величин оцениваются на основе проводимых экспериментов. Такими или близкими задачами занимается математическая статистика. Более точно математической статистикой называется наука, занимающаяся разработкой методов получения, описания и обработки опытных данных с целью изучения закономерностей случайных массовых явлений. Основное задание математической статистики состоит в том, чтобы на основе ограниченного числа наблюдений над массовыми явлениями выявить закономерности их поведения с целью дальнейшего прогнозирования. Сам термин “ статистика” может применяться в различных значениях. Статистика – это совокупность данных о множестве однородных объектов. Например, данные о количестве пассажиров, пользующихся метрополитеном в течение суток. Статистика – это совокупность методов обработки данных с целью представления полученной информации более наглядной и понятной. Статистика – это функция полученных экспериментальных значений, например, среднее арифметическое этих значений; число значений, превышающих определенную величину, и т. п. Именно в этом понимании термин “статистика” используется в математической статистике и будет использован в дальнейшем. В математической статистике можно выделить два направления: описательную статистику и индуктивную статистику (статистический вывод). Описательная статистика занимается накоплением, систематизацией и представлением опытных данных в удобной форме. Индуктивная статистика на основе этих данных позволяет сделать определенные выводы относительно объектов, о которых собраны данные, или оценки их параметров. Наиболее полезное применение математической статистики состоит в таком представлении результатов статистической обработки наблюдений, которое позволяет принимать решения, минимизирующие риск в условиях неопределенности. Типичными направлениями математической статистики являются:
6.2 Представление статистических данных При массовом промышленном производстве часто нужно без проверки каждого выпускаемого изделия установить, соответствует ли качество продукции стандартам. Если количество выпускаемой продукции очень велико или проверка продукции связана с приведением ее в негодность, то проверяется небольшое количество изделий. На основе этой проверки нужно дать заключение о всей серии изделий. Конечно, нельзя утверждать, что все транзисторы из партии в 1 млн. штук годны или негодны, проверив один из них. С другой стороны, поскольку процесс отбора образцов для испытаний, и сами испытания могут оказаться длительными по времени и привести к большим материальным затратам объем проверки изделий должен быть таким, чтобы он смог дать достоверное представление обо всей партии изделий, будучи минимальных размеров. Основным принципом математической статистики является принцип необходимой достаточности. Он состоит в том, что из всей совокупности элементов выбирают часть, которая подвергается исследованию (обработке). Результаты обработки экстраполируются на генеральную совокупность. Введем основные понятия математической статистики: генеральную совокупность и выборку.. Генеральной совокупностью называют всю совокупность всех изучаемых однородных объектов или экспериментальных данных. Будем обозначать через N число объектов или количество данных, составляющих генеральную совокупность. Величину N называют объемом генеральной совокупности. ЕслиN>>1, то есть N очень велико, то обычно считают N = ¥. Случайной выборкой или просто выборкой называют часть генеральной совокупности, наугад отобранную из нее. Слово "наугад" означает, что вероятность выбора любого объекта из генеральной совокупности одинакова. Это важное предположение, однако, часто трудно его проверить на практике. Объемом выборки называют число объектов или количество данных, составляющих выборку, и обозначаютn. Пример. Положим, что имеется, как указывалось ранее, партия транзисторов в 1 млн. штук, из которых 10 тысяч представляют брак. В действительности число бракованных изделий неизвестно. Для того чтобы можно было судить хотя бы приблизительно об относительной доле брака, отбирают и проверяют, например, 100 транзисторов. В этом примере генеральной совокупностью является исходная партия изделий в 1 млн. штук (N=1000000). Выборкой является множество транзисторов, изъятых из генеральной совокупности для контроля (n=100). Описанная процедура называется выборочным контролем качества. Выбор элементов генеральной совокупности можно организовать двумя способами: выбор без возвращенияи выбор с возвращением. В первом случае наугад выбирают все элементы выборки одновременно, затем выбранные элементы обследуются. Во втором случае отбор элементов производится поочередно. Каждый выбранный элемент обследуется и возвращается в генеральную совокупность, после чего наугад производится отбор следующего элемента и т. д. Заметим, что если объем выборки значительно меньше объема генеральной совокупности (n<<N), то различие исчезает. Определение. Выборка называется репрезентативной (представительной), если она несет в себе характерные признаки генеральной совокупности. Если элементы генеральной совокупности однородны, то выборка будет репрезентативной, если каждый элемент генеральной совокупности равновозможно может попасть в выборку. Метод исследования свойств генеральной совокупности по данным выборки называютвыборочным методом. В дальнейшем будем считать, что элементам выборки можно приписать соответственно числовые значениях1, х2, ... , хn. Например, в процессе контроля качества производимых биполярных транзисторов это могут быть измерения их коэффициента усиления по постоянному току. При
теоретико-вероятностном подходе
генеральная совокупность – это
случайная величина Х, заданная на
пространстве элементарных событий Числовые значения х1, х2, ... , ,хn будем рассматривать как значения случайной величины X . То естьпритеоретико-вероятностном взгляде выборка – это результат ограниченного ряда наблюдений х1, х2, ... , хnслучайной величины Х. Пусть имеются результаты измерения случайной величины Х с неизвестным законом распределения, которые представлены в виде таблицы: ТАБЛИЦА 6.1
Такую таблицу называют статистическим рядом. Статистический ряд представляет собой первичную форму записи статистического материала, и он может быть обработан различными способами. 6.2 Представление статистических данных
Пусть
теперь Х
– дискретная
случайная величина, принимающая
значения х1, х2,
... , хN ,
а х1, х2,
... , ,хn –
выборка, т.е. это значения случайной
величины, полученные в результате
проведения опытов.
Будем полагать, что
значение xj наблюдалось nj раз
Наблюдаемые
значения х1, х2,
... , хn называют вариантами,
а таблицу с упорядоченными по возрастанию
вариантами и соответствующими
относительными частотами ТАБЛИЦА 6.2
Из
определения относительной частоты
следует, что Если х1, х2, ... , хn – выборка реализаций непрерывной случайной величины Х или п>>1 (объем выборки большой) для дискретной случайной величины, то строится интервальный вариационный ряд. Методика его построения следующая.
1.
Определяются максимальное 2. Определяется размах вариационного ряда
3. Определяется количество интервалов
Если k – не целое, то kокругляется в большую сторону до ближайшего целого числа.
4.
Определяется оптимальная ширина
интервала
5. Определяются границы интервалов [aj, aj+1) следующим образом:
6.
Производится распределение вариантов
по интервалам таким образом, что
вариант
7. Для каждого интервала вычисляют представителя интервала
ТАБЛИЦА 6.3
Графическое
представление интервального ряда
носит название гистограммы. Гистограмма
строится следующим образом. По оси
абсцисс откладываются интервалы
[aj, aj+1)
и на каждой из них строится прямоугольник,
площадь которого равна относительной
частоте
Если число опытов увеличивать, то полученная гистограмма все более будет приближаться к плотности распределения случайной величины Х. Для исследования вида закона распределения случайной величины по выборке возникает необходимость в построении статистического аналога функции распределения. Такой статистический аналог функции распределения называется эмпирической (статистической) функцией распределения. Эмпирической функцией распределения F*(x) называется закон изменения частоты события X < x в данном статистическом материале, то есть
Для того чтобы найти значение статистической функции распределения при данном х, надо подсчитать число опытов, в которых случайная величина Х приняла значения меньше, чем х, и разделить на общее число произведенных опытов. Полученная таким образом статистическая функция распределения является очень грубым приближением функции распределения F(x) случайной величины Х и в таком виде не используется на практике. Она носит в каком-то смысле качественный характер, из которого можно выдвинуть гипотезу о законе распределения случайной величины Х. При увеличении числа опытов (n ®¥)F*(x) по вероятности сходится к F(x). Однако, с увеличением n построение F*(x) становится очень трудоемкой операцией. Поэтому на практике часто бывает удобно пользоваться статистической характеристикой, которая приближается к плотности распределения. По полученному статистическому материалу (вариационному ряду) можно построить график эмпирической функции распределения. Он имеет вид аналогичной теоретической функции распределения дискретной случайной величины – вид функцией скачков. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Лекция №7. Числовые характеристики выборки |




 (
(
 .
.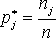 .
.
 .
Из построения следует, что площадь
суммы всех прямоугольников равна
единице. Очевидно, что если плавно
соединить левые точки прямоугольников
гистограммы, то полученная кривая
будет первым приближением к кривой
плотности распределения случайной
величины Х.
.
Из построения следует, что площадь
суммы всех прямоугольников равна
единице. Очевидно, что если плавно
соединить левые точки прямоугольников
гистограммы, то полученная кривая
будет первым приближением к кривой
плотности распределения случайной
величины Х.
