1.2. Фигура Земли и географическая система координат
Для определения местоположения ВС и других пунктов нужна система координат на земной поверхности. Свойства системы координат зависят от формы поверхности, на которой она задана. Поэтому необходимо выяснить, какую форму имеет Земля как планета.
Любое тело имеет форму, имеет ее и Земля. Поверхность, ограничивающая Землю как физическое тело, называется физической поверхностью Земли. Разумеется, эта поверхность носит сложный нерегулярный характер, обусловленный неровностями рельефа: горами, равнинами, впадинами. Любой человек может немного изменить физическую поверхность Земли, например, выкопав яму. Очевидно, что на такой поверхности ввести какую-либо приемлемую для практики систему координат невозможно. Необходимо эту поверхность каким-то образом «сгладить». Для этого используется понятие уровенной поверхности.
Уровенная поверхность – это поверхность, во всех точках перпендикулярная направлению силы тяжести (отвесной линии). Уровенных поверхностей бесконечно много, они проходят на разных высотах, не пересекаются между собой и практически параллельны. Разумно выбрать в качестве сглаженной фигуры Земли форму той из уровенных поверхностей, которая совпадает с физической поверхностью в морях и океанах, где нет неровностей рельефа. Такая фигура получила название геоида (рис.1.2).
Рис.1.2. Геоид и эллипсоид
Геоид(geoid) – это фигура, образованная уровенной поверхностью, совпадающей в морях и океанах с их средней поверхностью. В районах материков поверхность геоида проходит под уровнем рельефа местности и определить ее точное положение невозможно. Поэтому вместо нее используют поверхностьквазигеоида, которая совпадает с геоидом в морях и очень близка к нему на суше. Эту поверхность и называютсредним уровнем моря (Mean Sea Level, MSL), от которого отсчитывают высоту рельефа и другие высоты. В России за начало уровня отсчета высот принято нулевое деление футштока (мерной линейки), установленной в Обводном канале в Кронштадте.
Поверхности геоида и квазигеоида хотя и являются гладкими по сравнению с физической поверхностью Земли, но все же имеют неправильную форму. Это вызвано неравномерным расположением гравитационных масс в теле Земли, вследствие чего происходит отклонение отвесных линий. Поэтому на геоиде невозможно задать удобную систему координат (сетку меридианов и параллелей) и значит решать задачи, связанные с расчетом расстояний и направлений на поверхности земли. Для точного решения навигационных задач фигуру Земли аппроксимируют эллипсоидом вращения (ellipsoid).
Эллипс – это плоская фигура, которая относится к кривым второго порядка (рис.1.3)
Рис. 1.3. Эллипс и его параметры
Имеет большую a и малуюb полуоси. Основное свойство эллипса – сумма расстояний от любой точки эллипса до двух фиксированных точек F1 и F2, называемых фокусами, есть величина постоянная. Эллипс – это сжатая окружность или окружность, на которую «смотрят» не перпендикулярно ее плоскости.
В геодезии используется три системы координат: местная, геоцентрическая (привязанная к Земле) и эллипсоидальная.
Местная система координат. В отдельных странах или группе стран применяются при обработке геодезических измерений эллипсоиды, выведенные по результатам геодезических работ, охватывающих территорию данной страны или нескольких стран. Такие "рабочие" эллипсоиды называются референц-эллипсоидами. Система координат, определяемая на таком эллипсоиде, называется местной.
Референц-эллипсоид отличается от общего земного эллипсоида размерами и центр его не совпадает с центром Земли. Вследствие несовпадения центров рефренц-эллипсоидов и реальной Земли малая ось референц-эллипсоида не совпадает с осью вращения Земли (рис. 1.4).
Рис. 1.4. Различия между общеземным эллипсоидом и референц-эллипсоидом
Каждое государство старается выбрать такие параметры эллипсоида и так его разместить в теле Земли, чтобы его поверхность как можно ближе подходила к поверхности геоида на территории данного государства (при этом в других частях Земли отклонения могут быть большими). В России на протяжении многих лет используется эллипсоид Ф.Н. Красовского (a = 6378,245 км,b = 6356,86301877 км) на базе которого существовала системагеодезических координат(сетка меридианов и параллелей) СК-42, в которой координаты любой точки определяются: широтойB и долготой L (рис.1.4).
Геодезическая широта В –это угол, заключенный между плоскостью экватора и нормалью к поверхности эллипсоида в данной точке.
Геодезическая долгота – двугранный угол, заключенный между плоскостями начального меридиана и меридиана данной точки.
Поскольку координаты (широты и долготы, latitudes and longitudes) задаются на поверхности референц-эллипсоида, одна и та же точка на Земле будет иметь разные координаты в разных странах. И наоборот, одни и те же численные значения B иL будут соответствовать разным точкам на картах разных стран. Это создает сложности для международной аэронавигации, поэтому ИКАО приняло решение с 1 января 1998 г. публиковать в документах аэронавигационной информации координаты пунктов в единой для всего мира системе координат, называемой WGS-84 (World Geodethic System).
В РФ используется практически идентичная WGS-84 система координат- ПЗ-90.02 (Параметры Земли), в которой используется геоцентрическая (привязанная к Земле) система координат (X, Y, Z), началом которой является центр массы Земли S (геоцентр, т.е. центр массы, включая массу атмосферы) (рис. 1.5.). Ось Z совпадет с осью вращения Земли.
Ось вращения Z
Рис. 1.5. Привязанная к центру Земли пространственная прямоугольная система
координат (X, Y, Z), используемая в системах WGS-84 и ПЗ-90.02.
Геоцентрическая система координат используется при определении места воздушного судна при решении системы уравнений.
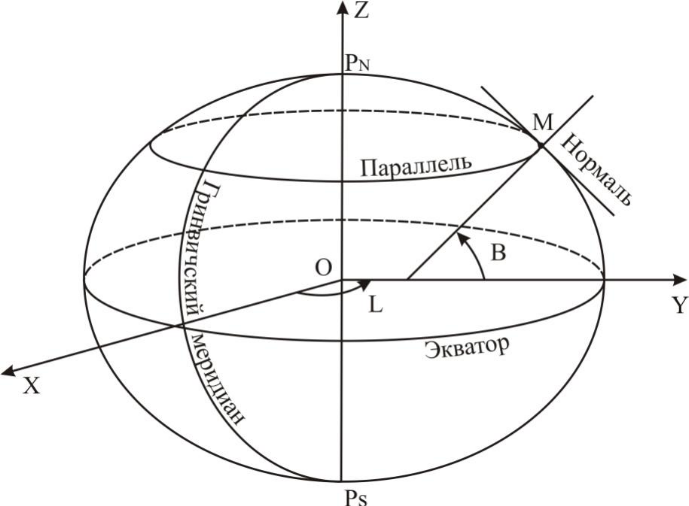
Рис. 1.4. Геодезические координаты
Если очень высокая точность решения навигационных задач не требуется, то Землю можно рассматривать как сферу. В этом случае используется нормальная сферическая система координат, полюсы которой совпадают с географическими полюсами нашей планеты, т.е. точками, в которых ось вращения Земли пересекает ее поверхность. Система координат на сфере строится с помощью больших кругов.
Большим кругом (Great Circle, G/C) называется окружность, образующаяся в результате сечения сферы плоскостью, проходящей через центр сферы.
Радиус большого круга равен радиусу самой сферы. Он называется большим, поскольку на сфере нельзя нарисовать окружность с радиусом еще большим. Все другие круги на сфере называются малыми.
Экватор (equator) –- большой круг, плоскость которого перпендикулярна оси вращения Земли (рис. 1.5).
Рис. 1.5. Сферические координаты
Меридиан(meridian) – большой круг, плоскость которого проходит через ось вращения Земли.
Параллель(parallel) – малый круг, плоскость которого перпендикулярна оси вращения (параллельна экватору).
Экватор на Земле один, а меридианов бесчисленное множество – ведь через каждую точку можно провести свой меридиан. Все они одинаковы и равноправны, поэтому условно один из них выбирают в качестве начального. В качестве начального меридиана используется Гринвичский меридиан (Greenwich meridian), который когда-то проходил через расположенную вблизи Лондона Гринвичскую обсерваторию (сейчас обсерватория переехала на другое место, но меридиан сохранился). В XIX веке в разное время в 30 качестве начального использовали и другие меридианы (Парижа, острова Ферро в Атлантическом океане, Пулковской обсерватории под Петербургом).
Широтой φ (сферической широтой) точки на поверхности земной сферы называется угол, заключенный между плоскостью экватора и направлением из центра сферы в данную точку.
Широта изменяется от 90° южной широты до 90° северной широты. При расчетах по формулам северную широту можно считать положительной, а южную отрицательной. На экваторе широта равна нулю, а на географических полюсах ±90°.
Долготой λ (сферической долготой) точки на поверхности сферы называется двугранный угол, заключенный между плоскостями начального меридиана и меридиана данной точки.
Этот угол можно показать как плоский в плоскости экватора (рис.1.5).
Долгота изменяется от 180° западной долготы до 180° восточной. При расчетах по формулам им также можно приписывать знаки соответственно минус и плюс (или наоборот, как это принято, например в США).
Единицами измерения широты и долготы являются угловые градусы, минуты и секунды, а иногда и их десятичные доли (десятые, сотые и т.д.). За рубежом используются следующие буквенные обозначения:
N (north) – север, S (south) – юг, E (east) – восток, W (west) – запад.
Моряки используют эти же обозначения, но не на английском, а на голландском языке для обозначения основных направлений по сторонам света: норд, зюйд, ост и вест.
Одни и те же значения широты и долготы в документах аэронавигационной информации при выполнении различных навигационных расчетов могут быть представлены по-разному:
37º 23' 12'' с.ш. = N37º 23.2' = +37.38667º.
134º 45' 45'' з.д. = W134º 45.75' = -134.7625º.
На картах нанесена сетка меридианов и параллелей, с помощью которой можно определить координаты точки или найти точку с известными координатами. Для того, чтобы это можно было сделать точнее, на обрезах карты, а на аэронавигационных картах – и на самих меридианах и параллелях, сделаны промежуточные деления (рис. 1.6).
Ни направление нормали к поверхности эллипсоида, ни направление к центру Земли непосредственно приборами измерены быть не могут, поэтому не могут быть непосредственно измерены ни геодезическая, ни сферическая широты. Непосредственно можно определить лишь направление отвесной линии. В связи с этим используется также астрономическая система координат, в которой астрономическая широта – угол, заключенный между плоскостью экватора и отвесной линией в данной точке. Различия между геодезическими, нормальными сферическими и астрономическими координатами невелики – не более нескольких угловых минут. Поэтому, когда различие между этими системами координат не играет роли, их объединяют общим названием - географические координаты.
Кроме особо оговоренных случаев Земля принимается за сферу и в качестве географических используются сферические широта и долгота.
Длина дуги большого круга (в частности, экватора и меридиана) протяженностью в 1° в среднем равна 111,2 км. Именно в среднем, потому, что на самом деле меридиан является не окружностью, а эллипсом и длина дуги в 1° различна на разных широтах. Соответственно, длина дуги в одну минуту составляет в среднем 1852 м, а секунды – около 31 м.
Длина параллели, которая является не большим, а малым кругом, уменьшается по мере приближения к полюсу, т.е. с увеличением широты. Длина дуги в 1° на параллели с широтой φ составляет 111,2*cos φ .
Рис.1.6. Определение широты и долготы по карте
Расстояния на земной поверхности измеряются в метрах, километрах, а за рубежом часто и в морских милях (nautical miles, NM). Величина морской мили соответствует средней длине одной минуты меридиана. В морской и воздушной навигации принято фиксированное значение длины морской мили (м.мили) – 1852 м, ведь единица измерения не должна быть разной на различных широтах.
Высоты измеряются в метрах, за рубежом часто в футах.
1 м.миля = 1,852 км; S км =1,852* S м.миль.
1 м = 3,2808 фт; Н фт = 3,2808 Н м.