3. Требования к выполнению и оформлению расчётно-графической работы

Выполненная расчётно-графическая работа должна содержать:

1. Титульный лист.

2. Расчётно-пояснительную записку.

3. Список используемой литературы.

Образец выполнения титульного листа показан на рис. 3.1.

В пояснительную записку входят:

1. Задание на расчётно-графическую работу, которое оформляется на первом листе записки и содержит электрическую схему, исходные данные к расчёту и перечень пунктов, которые необходимо выполнить. Образец оформления первого листа приведён на рис 3.2.

2. Расчёты, чертежи схем, программу расчёта уравнений на калькуляторе (если последняя использовалась при выполнении расчётно-графической работы). Расчёт должен сопровождаться пояснительным текстом и ссылками на литературу. При выполнении каждого пункта задания исходная, либо преобразованная электрическая схема чертится заново со всеми необходимыми обозначениями.

При расчёте следует использовать полную форму записи, которая должна содержать формулу, исходные численные значения, результат и размерность.

Например:

P₁ = R₁ I₁² = 10 ∙ 5² = 250 Вт

Такая форма записи облегчает самоконтроль при выполнении расчётов.

3. Сводная таблица результатов.

Таблица должна содержать перечень методов, которыми была рассчитана электрическая цепь, и результаты расчёта токов различными методами.

Федеральное агенство по образованию

Государственное образоватетельное учреждение

высшего профессионального образования

«Курский государственный технический университет»

Кафедра «Электротехники, электроники и автоматики»

Расчётно-графическая работа №1

Расчёт электрической цепи постоянного тока

Выполнил ст. гр. АХ 61 Петров Ю.К.

Проверил асс. Иванов К.Л.

Курск 2009

Рис.3.1

4. Список используемой литературы.

Список приводится на последней странице расчётно-пояснительной записки.

Например:

1. Касаткин А.С, Немцов В.М. Электротехника. – М. :Энергоатомиздат, 2003.

2. Конспект лекций доц. Иванова О.Г.

Расчётно-пояснительная записка оформляется на листах А4 с учётом требований ЕСКД. Листы записки должны быть скреплены и вшиты в обложку из плотной бумаги.

Все элементы электрической схемы следует изображать в соответствии с ГОСТ 2721-88 и ГОСТ 2750-88, используя чертёжные инструменты (линейка, трафареты, циркуль и т.д.). Около условных графических обозначений схемы необходимо поставить буквенные обозначения параметров ( резистивный элемент R, E – источник э.д.с. и т.д.). Узлы электрической схемы могут быть обозначены буквами латинского алфавита a, b, c, d либо цифрами 1, 2, 3….

При обозначении токов – I, сопротивлений – R, напряжений – U, потенциалов - φ и т.д. в различных ветвях схемы необходимо использовать индексы. В качестве нижних индексов могут применяться арабские или римские цифры, строчные буквы латинского, русского или греческого алфавитов.

Например:

R_1, E_2, U_ab.

В качестве верхних индексов допускаются штрихи и римские цифры.

Например: I^Ι, U^ΙΙ.

В случае, когда одним обозначением заменяется разность двух величин, первая буква или цифра индекса относится к уменьшаемому, а вторая - к вычитаемому.

Например: φ_1─φ₂ = U₁₂.

Применение индексов с тремя и более цифрами или буквами не рекомендуется.

Вариант 525

Схема электрической цепи постоянного тока

E1	E2	R1	R2	R3	R4	R5	R6
В	В	Ом	Ом	Ом	Ом	Ом	Ом
19	14	6	8	10	5	9	7

Таблица исходных данных

1. Рассчитать токи во всех ветвях схемы c применением законов Кирхгофа.

2. Рассчитать ток в ветви «cd» методом эквивалентного генератора.

3. Преобразовать схему к двум узлам, рассчитать токи во всех ветвях преобразованной схемы методом напряжения между двумя узлами.

4. Привести таблицу результатов расчёта

Рис 3.2 Образец оформления первого листа расчётно-графической работы

Приложение 1

Расчёт токов в ветвях схемы применением законов Кирхгофа

Применим законы Кирхгофа для определения токов ветвей схемы цепи рис. П.1.1,если э.д.с. и сопротивления её элементов заданы.

Число неизвестных токов схемы равно числу m её ветвей. Поэтому для решения задачи необходимо составить систему, состоящую из m=6 независимых уравнений. Число независимых уравнений, которые можно составить по первому закону Кирхгофа, равно числу узлов схемы без одного (в схеме рис.П.1 – 3 уравнения):

для узла a: I₁ + I₅ + I₆ = 0

для узла c: I₄ – I₆ – I₃ = 0

(П.1.1)

для узла d: I₃ – I₁ – I₂ = 0

Недостающее число уравнений (для схемы рис.П.1.1 – 3 уравнения) составляем, пользуясь вторым законом Кирхгофа для замкнутых независимых контуров. Выберем три независимых контура, как указано на схеме рис. П.1.1, и примем обход их по направлению движения часовой стрелки. Тогда по второму закону Кирхгофа, получим:

для контура 1: R₁I₁ – R₅I₅ – R₂I₂ = E₁ – E₂

для контура 2: R₂I₂ + R₄I₄ + R₃I₃ = E₂

(П.1.2)

для контура 3: R₅I₅ – R₆I₆ – R₄I₄ = 0

Используем для решения полученной системы уравнений (П.1.1) и (П.1.2) метод Гаусса.

Из уравнений (П.1.2) исключаем токи:

I₂ = I₃ – I₁

I₄ = I₃ + I₆

I₅ = – I₁ – I₆

и получаем систему уравнений:

(R₁ + R₂ + R₃)I₁ – R₂I₃ + R₅I₆ = E₁ – E_2,

– R₂I₁ + (R₂ + R₃ +R₄)I₃ + R₄I₆ = E_2, ( П.1.3)

R₅I₁ + R₄I₃ + (R₄ + R₅ + R₆)I₆ = 0.

Рис. П.1.1 Схема сложной цепи для определения токов ветвей по законам Кирхгофа

Приложение 2

Расчёт тока в ветви «cd» методом эквивалентного генератора.

Возьмем электрическую цепь, используемую в предыдущих примерах (рис. П.2.1). Для определения э.д.с. эквивалентного генератора создаём режим холостого хода, т.е. размыкаем ветвь «cd» (рис. П.2.2). Напряжение U_хх определяем относительно точек «cd». Для этого по второму закону Кирхгофа запишем уравнение для контура «cdec».Задавшись направлением токов I₆^/ и I₄^/ с учётом правила, что ток течёт от «+» источника к «–», получаем уравнение:

(П.2.1)

Токи I₄ и I₆ определяем, используя метод напряжения между двумя узлами. Из рис. П.2.2 видно, что разорвав ветвь с элементом R₅ , получаем схему, содержащую параллельные ветви относительно узлов «e» и «b». Следовательно:

(П.2.2)

Зная значение U_eb, определяем токи I₄^/ и I₆^/, входящие в уравнение П.2.1:

(П.2.3)

(П.2.4)

Подставив найденные из уравнений П.2.3 и П.2.4 значения токов в уравнение П.2.1, определяем .

Для определения сопротивления эквивалентного генератора ветвь «cd» оставляем разомкнутой, источники э.д.с. шунтируем, а источники тока размыкаем. Так для рассматриваемого примера получаем схему рис. П.2.3, в этой схеме требуется определить сопротивление относительно узлов «c» и «d». Поскольку относительно узлов «c» и «d» нет параллельно и последовательно включенных элементов, треугольник сопротивлений R₂, R₃, R₄ (рис. П.4.3) преобразовываем в эквивалентную звезду . После преобразования внутреннее сопротивление эквивалентного генератора определится по формуле:

(П.2.5)

После сделанных расчётов можно схему, обведённую пунктиром, на рис. П.2.1 заменить двумя последовательно соединёнными элементами и, т.е. эквивалентным генератором. Нагрузкой генератора является элемент(рис. П.2.4). Требуемый ток в ветви «cd» определяется из схемы рис. П.2.4:

(П.2.6)

Рис. П.2.1

Рис. П. 2.2

Рис. П.2.3

Рис. П.2.4

Расчёт электрической цепи методом эквивалентного генератора

Приложение 3

Расчёт токов методом напряжения между двумя узлами.

При расчёте данным методом требуется вначале привести исходную схему к схеме, содержащей только два узла. Так как приведённые в задании схемы не содержат параллельно и последовательно соединённых элементов, то для того, чтобы их привести к двум узлам, необходимо сделать преобразование треугольника сопротивлений в эквивалентную звезду или наоборот - звезды в треугольник. Так для схемы рис.П.3.1 в результате преобразования треугольника сопротивлений в эквивалентную звезду, получим схему, содержащую только параллельные ветви, т.е. два узла (см. рис.П.3.1 и П.3.2).

Используя известное уравнение для расчёта напряжения между двумя узлами, получаем:

.

Определив напряжение между узлами a и b, определяем токи в ветвях электрической цепи:

,

,

.

Рис. П. 3.1

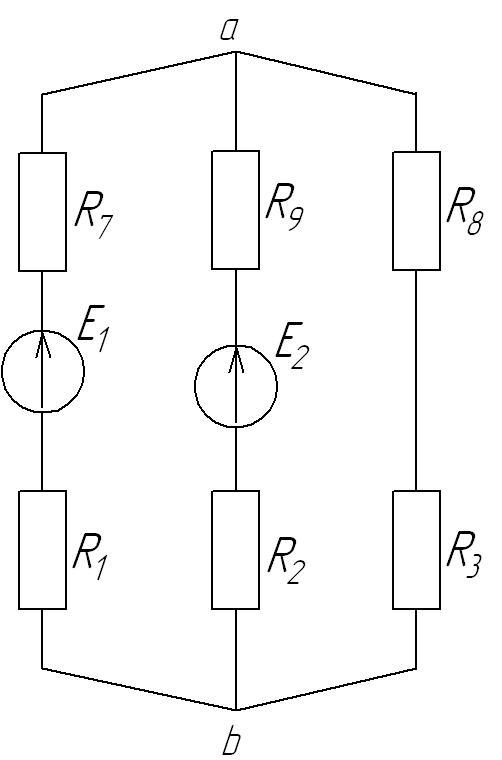
Рис. П. 3.2