2.4.4. Смачивание

Смачивание – взаимодействие жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздух).

При нанесении небольшого количества жидкости на поверхность твердого тела или на поверхность другой жидкости, имеющей большую плотность, возможно два случая: в первом случае жидкость приобретает форму капли, в другом случае растекается. Рассмотрим первый процесс, когда капля не растекается по поверхности другого тела (рис. 2.4).

Рис. 2.4. Смачивание на границе раздела трех фаз

Рассмотрим каплю жидкости на поверхности твердого тела в условиях равновесия. Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил.

На единицу длины периметра действуют три силы:

1. Поверхностная энергия твердого тела, стремясь уменьшиться, растягивает каплю по поверхности. Эта энергия равна поверхностному натяжению твердого тела на границе с воздухом σ_ТГ.

2. Поверхностная энергия на границе твердого тела с жидкостью σ_ТЖ стремится сжать каплю, т.е. поверхностная энергия уменьшается за счет снижения площади поверхности.

3. Поверхностная энергия на границе капли жидкости с воздухом σ_ЖГ направлена по касательной к сферической поверхности капли.

Угол θ, образованный касательными к межфазным поверхностям, ограничивающим смачиваемую жидкость, и имеющий вершину на линии раздела трех фаз, называется краевым углом или углом смачивания.

Проекция вектора σ_ЖГ на горизонтальную ось – произведение σ_ЖГ · cos θ.

В условии равновесия:

σ_ТГ = σ_ТЖ + σ_ЖГ·cosθ, (2.14)

отсюда

. (2.15)

Полученное соотношение (2.15) называют уравнением Юнга.

2.4.4.1. Анализ уравнения Юнга

1. Если σ_ТГ > σ_ТЖ, то cos θ > 0 и θ < 90° (краевой угол смачивания) острый – смачивание.

Пример: вода на поверхности металла, покрытого оксидной пленкой. Чем меньше угол θ и больше cos θ, тем лучше смачивание.

2. Если σ_ТГ < σ_ТЖ, то cos θ < 0 и θ > 90° (краевой угол смачивания тупой) – несмачивание.

Пример: вода на парафине или тефлоне.

3. Если σ_ТГ = σ_ТЖ, то cos θ = 0 и θ = 90° – граница между смачиваемостью и несмачиваемостью.

4. Если , тоcos θ = 1 и θ = 0° – полное смачивание (растекание) – капля растекается в тонкую пленку.

Пример: ртуть на поверхности свинца, очищенного от оксидной пленки.

Рис. 2.5. Несмачивание

Полного несмачивания, т.е. такого положения, когда θ = 180°, не наблюдается, т.к. при соприкосновении конденсированных тел поверхностная энергия всегда уменьшается.

Смачиваемость водой некоторых твердых тел характеризуется следующими краевыми углами: кварц – 0°, малахит – 17°, графит – 55°, парафин – 106°. Хуже всего смачивается водой тефлон, краевой угол смачивания – 120°.

Различные жидкости неодинаково смачивают одну и ту же поверхность. Согласно приближенному правилу – лучше смачивает поверхность та жидкость, которая ближе по полярности к смачиваемому веществу.

По виду избирательного смачивания все твердые тела делят на три группы:

• Гидрофильные (олеофобные) материалы – лучше смачиваются водой, чем неполярными углеводородами: кварц, силикаты, карбонаты, оксиды и гидроксиды металлов, минералы (краевой угол меньше 90° со стороны воды).

• Гидрофобные (олеофильные) материалы – лучше смачиваются неполярными жидкостями, чем водой: графит, уголь, сера, парафин, тефлон.

Таблица 2.3

Зависимость свойств поверхности от краевого угла смачивания

θ	cos θ	Процесс	Поверхность
θ = 0°	cos θ = 1	Растекание	Гидрофильная (олеофобная)
θ < 90°	cos θ > 0	Смачивание	Гидрофильная (олеофобная)
θ = 90°	cos θ = 0	Граница между смачиваемостью и несмачиваемостью
θ > 90°	cos θ < 0	Несмачивание	Олеофильные (гидрофобные)

Получим зависимость между краевым углом смачивания и работой адгезии. Для этого заменим числитель в уравнении Юнга через работу адгезии из уравнения Дюпре (2.12):

. (2.16)

Уравнение (2.16) показывает, что краевой угол определяется конкуренцией двух факторов. Первый фактор – молекулярное притяжение жидкости к твердой поверхности: чем сильнее это притяжение, тем больше работа адгезии. Второй фактор – взаимное притяжение молекул жидкости, количественной мерой которого является поверхностное натяжение.

Из уравнения (2.16) следует, что при преобладании притяжения жидкости к твердой подложке (при W_A > σ_ЖГ), cos θ > 0, жидкость смачивает поверхность. Напротив, если сильнее взаимное притяжение молекул жидкости (σ_ЖГ > W_A) , то cos θ < 0, случай несмачивания. Следовательно, жидкости с небольшим поверхностным натяжением лучше смачивают твердые тела, чем жидкости с небольшим поверхностным натяжением. Многие органические жидкости и сжиженные газы полностью смачивают большинство твердых материалов.

Пример 2.1. Рассчитайте коэффициент растекания жидкости СН₂J₂ по полиэтилену. Объясните знак коэффициента растекания.

, θ = 46°.

Решение:

1. Рассчитаем работу когезии растекающейся жидкости по уравнению (2.11):

.

2. Рассчитаем работу адгезии между СН₂J₂ и полиэтиленом, используя уравнение (2.16):

,

следовательно,

.

Так как , то,отсюда

.

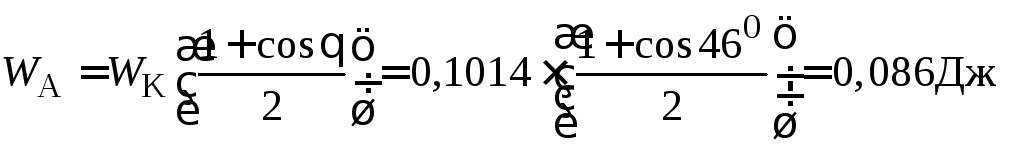3. Рассчитаем коэффициент растекания по уравнению (2.13):

,

следовательно, СН₂J₂ по полиэтилену не растекается.

Рассмотренные закономерности смачивания выполняются на всех поверхностях жидкостей и только на идеально гладких поверхностях твердых тел. На поверхностях реальных твердых тел обязательно имеются шероховатости, неоднородности, поры, трещины и т.д. Основное следствие шероховатости – площадь такой поверхности (S_ш) больше, чем площадь гладкой подложки (S₀). Отношение S_ш/S₀ = К называют коэффициентом шероховатости К > 0.

Влияние шероховатости на краевой угол описывается уравнением Венцеля – Дерягина:

. (2.17)

Из уравнения (2.17) следует, что для смачивающих жидкостей (cosθ > 0) шероховатость приводит к уменьшению краевых углов (cos θ_ш > cos θ). В случае несмачивания шероховатость вызывает увеличение краевых углов (cosθ_ш < cosθ). Таким образом, на гидрофильных поверхностях шероховатость улучшает смачивание, на гидрофобных – ухудшает. Пример: ворсинки на перьях водоплавающих птиц значительно увеличивают шероховатость их поверхности, это способствует тому, что перья практически не смачиваются водой.

Смачиваемость частиц пыли водой оказывает влияние на эффективность мокрых пылеуловителей, особенно при работе с рециркуляцией. Гладкие частицы пыли смачиваются лучше, чем частицы с неровной поверхностью, т.к. последние в большой степени оказываются покрытыми адсорбированной газовой оболочкой, затрудняющей смачивание.

Пример 2.2. Определите краевой угол смачивания, образованный каплей воды на твердом теле, если поверхностное натяжение на границе воздух–твердое тело, вода–твердое тело и вода–воздух соответственно равны: 0,057; 0,020; 0,074 Дж/м². Будет ли вода смачивать данную поверхность?

Решение:

По закону Юнга: .

cos θ < 0 и θ > 90° – данная поверхность водой не смачивается.