
06-09-2015_14-13-46 / Матрицы. Таможня. 2015
.docxГЛАВА 1. Элементы линейной алгебры.
§ 1. Матрицы.
-
Основные понятия
Матрицей
называется прямоугольная
таблица, составленная из элементов
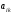 некоторого множества:
некоторого множества:![]()
 или
или

Первый индекс
обозначает номер строки, второй — номер
столбца, в которых стоит выбранный
элемент.![]()
Матрица
имеет размерность
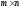 ,
если у
неё
,
если у
неё
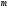 строк и
строк и
 столбцов.
столбцов.
Для обозначения
матриц употребляются символы:
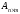 ,
,
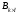 ,
,
 ,
,
 ,
,
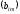 ,
,
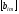 ,
,
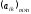 и т.д.
и т.д.
Квадратными
порядка
 называются
матрицы,
у которых число строк равно числу
столбцов, т.е.
называются
матрицы,
у которых число строк равно числу
столбцов, т.е.
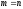 .
.![]()
В частности, матрица порядка 1 отождествляется с её элементом, т.е. любое число — частный случай матрицы.
Главную
диагональ
квадратной матрицы составляют её
элементы
 ,
,
 ,…,
,…,
 .
.![]()
![]()
Диагональной
называется
квадратная матрица,
у которой
все недиагональные элементы равны нулю
(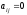 при
при
 ).
).
Например,

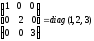 —
диагональная квадратная матрица
размерности 3 с элементами 1, 2, 3 по
главной диагонали.
—
диагональная квадратная матрица
размерности 3 с элементами 1, 2, 3 по
главной диагонали.![]()
![]()
Единичной
называется
диагональная матрица,
все элементы которой равны единице;
единичная матрица
обозначается
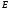 или
или
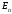 ,
где
,
где
 — порядок матрицы.
— порядок матрицы.
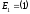 ,
,
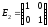 ,
,
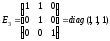 .
.
Ступенчатой
называется
матрица:![]()
 ,
где
,
где
 .
.
Например,
 —
не ступенчатая,
—
не ступенчатая,![]()
 — ступенчатая.
— ступенчатая.![]()
Верхней (нижней) треугольной матрицей называется квадратная матрица, все элементы которой, расположенные ниже (выше) диагонали равны нулю.
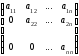 — верхняя
треугольная матрица;
— верхняя
треугольная матрица;
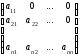 — нижняя треугольная
матрица.
— нижняя треугольная
матрица.
Например,
 — верхняя треугольная матрица,
— верхняя треугольная матрица,
 —
нижняя
треугольная матрица.
—
нижняя
треугольная матрица.![]()
![]()
Нуль-матрицей
(нулевой матрицей)
размерности
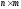 ,
обозначаемой
,
обозначаемой
 ,
называется
матрица,
все элементы которой равны нулю.
,
называется
матрица,
все элементы которой равны нулю.![]()
Равными,
называются
матрицы
 и
и
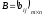 ,
если они
имеют одинаковые размерности, т.е.
,
если они
имеют одинаковые размерности, т.е.
 ,
,
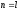 и элементы этих матриц, занимающие одну
и ту
же позицию,
равны,
т.е.
и элементы этих матриц, занимающие одну
и ту
же позицию,
равны,
т.е.
 .
.![]()
Например, если
 ,
,
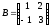 ,
то
,
то
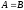 .
.![]()
![]()
1.2 Основные операции над матрицами
![]()
Сложение
матриц.
Суммой двух матриц
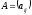 и
и
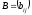 одной и той же размерности
одной и той же размерности
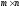 называется матрица
называется матрица
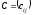 той же размерности такая, что
той же размерности такая, что
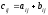 .
.
Итак, можно
складывать только
матрицы одной и той же размерности.
При сложении матриц складываются
соответствующие
элементы.![]()
Пример
1.6. Найдите
сумму матриц
 и
и
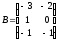 .
.
 — нуль-матрица
размерности
— нуль-матрица
размерности
 .
.![]()
![]()
![]()
Из определения суммы следует, что сложение матриц подчинено:
а) коммутативному
закону
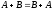 ;
;
б) ассоциативному закону
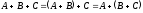 ;
;
в)
 — закон поглощения нуля.
— закон поглощения нуля.
Умножение
матрицы на число.
Произведением матрицы
 на число
на число
 (или
(или
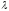 на матрицу
на матрицу
 )
называется матрица
)
называется матрица
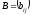 ,
где
,
где
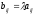 ,
т.е. при умножении матрицы на число надо
все элементы матрицы умножить на это
число.
,
т.е. при умножении матрицы на число надо
все элементы матрицы умножить на это
число.![]()
Пример 1.7.
2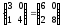 .
.![]()
![]()
Свойства
операции умножения
матрицы на число:![]()
а)
 (ассоциативность);
(ассоциативность);
б)
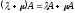 (дистрибутивность
относительно сложения чисел);
(дистрибутивность
относительно сложения чисел);
в)
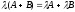 (дистрибутивность
относительно сложения матриц);
(дистрибутивность
относительно сложения матриц);
г)
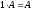 .
.
Пример 1.8.
Найдите
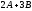 ,
где
,
где
 ,
,
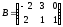 .
.

![]()
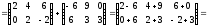
 .
.![]()
![]()
Умножение
матриц.(для
самостоятельного ознакомления)
Произведением матрицы
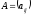 размерности
размерности
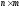 на матрицу
на матрицу
 размерности
размерности
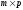 называется
матрица
называется
матрица
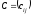 размерности
размерности
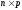 такая, что
такая, что
 ,
,
 ,
,
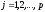 .
.
Умножать матрицы
 и
и
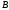 можно лишь в том случае, когда число
столбцов первого сомножителя
можно лишь в том случае, когда число
столбцов первого сомножителя
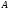 (число элементов в каждой строке матрицы
(число элементов в каждой строке матрицы
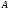 )
совпадает
с числом строк второго сомножителя
)
совпадает
с числом строк второго сомножителя
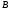 (число элементов в каждом столбце
(число элементов в каждом столбце
 ).
В частности для квадратных матриц
одинакового порядка определены оба
произведения
).
В частности для квадратных матриц
одинакового порядка определены оба
произведения
 и
и
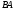 ,
и матрицы произведения являются
матрицами того же порядка
,
и матрицы произведения являются
матрицами того же порядка![]()
Пример
1.9. Пусть
 ,
,
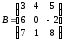 .
Найдите произведения
.
Найдите произведения
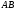 и
и
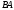 (если это возможно).
(если это возможно).



![]()


 .
.
Произведение
 не существует, так как число столбцов
матрицы
не существует, так как число столбцов
матрицы
 не совпадает с числом строк матрицы
не совпадает с числом строк матрицы
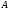
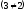 .
.![]()
Пример
1.10. Пусть
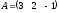 ,
,
 .
Найдите произведения
.
Найдите произведения
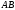 и
и
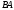 (если это возможно).
(если это возможно).
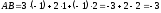 .
.
 .
.![]()
![]()
Из приведенных
выше
примеров
ясно, что в общем случае
 .
.
Коммутирующими
называют матрицы
 и
и
 ,
если для
них
выполнено условие
,
если для
них
выполнено условие
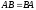 .
.
Свойства
операции умножения
матриц:![]()
а) ассоциативность:
если
определено одно из произведений
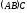 или
или
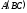 ,
то определено также и
второе
произведение,
и имеет место выше
приведённое равенство
,
то определено также и
второе
произведение,
и имеет место выше
приведённое равенство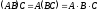 ;
;
б) дистрибутивность:
если
 — такая
матрица, что определено произведение
— такая
матрица, что определено произведение
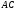 ,
то определены
произведения
,
то определены
произведения
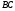 и
и
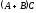 и верно равенство
и верно равенство
 (
(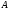 и
и
 — матрицы одинаковых размеров);
— матрицы одинаковых размеров);
в)
дистрибутивность:
если
 — такая
матрица, что определено произведение
— такая
матрица, что определено произведение
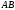 ,
то определены произведения
,
то определены произведения
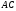 и
и
 и верно равенство
и верно равенство
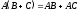 (
( и
и
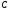 — матрицы одинаковых размеров);
— матрицы одинаковых размеров);
г)
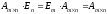 .
.
1.3 Транспонированная матрица
Транспонированием
матрицы называется такое её
преобразование, при котором строки
этой матрицы становятся её
столбцами с теми же номерами.![]()
 ,
,
 .
.
Транспонированная
матрица обозначается
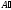 или
или
 .
.![]()
Свойства операции транспонирования:
-
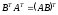 ;
2.
;
2.
 .
.
Если
 ,
т.е.
,
т.е.
 ,
то
матрица называется симметрической.
,
то
матрица называется симметрической.![]()
Пример1.11.
Транспонируйте
матрицу
 .
.
 .
.![]()
![]()
1.4 Элементарные преобразования матрицы.
![]()
Преобразования матрицы являются элементарными, если:
а) все строки заменить столбцами;
б) поменять местами две строки (два столбца);
в) умножить каждый элемент строки (столбца) на один и тот же множитель, отличный от нуля;
г) прибавить к элементам одной строки (столбца) соответствующие элементы другой строки (другого столбца), умноженные на один и тот же множитель.
Эквивалентными
называются матрицы
 и
и
 ,
если одна из другой получаются с помощью
элементарных преобразований.
Эквивалентность матриц
,
если одна из другой получаются с помощью
элементарных преобразований.
Эквивалентность матриц
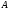 и
и
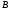 обозначают
следующим образом:
обозначают
следующим образом:
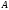 ~
~ .
.
Пример 1.13. Привести матрицу к ступенчатому виду с помощью элементарных преобразований:
.

 ~
~
 ~
~
![]()
![]()
~ .
.
§ 2. Определители.
2.1. Основные понятия
2.2. Свойства определителей
1. Определитель
не изменится, если строки определителя
заменить столбцами, а столбцы —
соответствующими строками.![]()
![]()
2. Общий множитель
элементов любой
строки (или столбца) может быть вынесен
за знак определителя.![]()
3. Если элементы
одной строки (столбца) определителя
соответственно равны элементам другой
строки (столбца), то определитель равен
нулю.![]()
4. При перестановке
двух строк (столбцов) определитель
меняет знак на противоположный.![]()
5. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственно элементы другой строки (столбца), умноженные на одно и то же число.
