Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3392_EI

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

562.2 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Если заполненное большинство клеток таблицы образует какую-то кривую, то искать линейную связь между Х и Y не имеет смысла.

Выборочный коэффициент корреляции rв характеризует степень корреляции (связи) между Х и Y и изменяется в пределах 0 ≤ | rв | ≤ 1. При rв = 0 корреляция между Х и Y отсутствует, а при | rв | = 1 корреляция между Х и Y переходит в функциональную связь.

В предположении линейной корреляции между Х и Y rв рассчитывается по формуле

∑(nxy )l xl yl − nxв yв

rв =

(l )

(2.21)

nσ хσ у

где хв

определяется

по

формуле

(2.8), а ув –

по аналогичной

формуле; σх

рассчитывается по формулам (2.9), (2.10), а σу – по аналогичным формулам.

В качестве примера найдем rв из данных таблицы 1:

∑(nxy )l xl yl = 3 10 4 + 2 14 4 + 4 14 6 + 5 18 6 +1 10 8 + 6 18 8 + 2 22 8 = 2404;

366

xв

(4 10 + 6 14 +11 18 + 2 22) =

≈ 15,913;

146

ув

(5 4 + 9 6 +

9 8) =

≈ 6,3478;

Dх

{(10 −15,913)2 4 + (14 −15,913)2 6 + (18 −15,913)2 11+ (22 −15,913)2 2}≈12,34;

σ х

Dх ≈ 3,513;

Dу

{(4 − 6,3478)2

5 + (6 − 6,3478)2 9 + (8 − 6,3478)2 9}≈ 2,314;

σу ≈ 1,521.

По формуле (2.21) находим rв:

rв =	2404− 23 15,913 6,3478	= 0,657 .
	23 3,513 1,521

Можно сделать вывод, что между Х и Y имеется заметная корреляция.

11.Условным математическим ожиданием дискретной случайной величины Y при

Х= х, где х – определенное значение случайной величины Х, называется произведение возможных значений Y на их условные вероятности:

M[Y | X = x]= ∑m yi p(yi | x).

i=1

Как видно из формулы, условное математическое ожидание M[Y | x] является функцией от х:

M[Y | x] = f(x),

которую называют функцией регрессии Y на Х.

Аналогично определяется условное математическое ожидание дискретной случайной величины Х и функция регрессии Х на Y:

M[X | y] = ϕ(у).

Величины M[Y | x] и M[Х | у] обозначаются, собственно как ух и ху .

Уравнения ух = f (x) и ху = ϕ ( y) называются эмпирическими или выборочными

линиями регрессии Y на Х и Х на Y соответственно.

В случае линейной корреляции между Х и Y эти линии будут прямыми и определяются уравнениями:

−yв

−xв

=rв σ y (x − xв );

σx

=rв σ x (y − yв ).

σу

(2.22)

(2.23)

РЕШЕНИЕ ТИПОВОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

Дана двумерная выборка дискретных случайных величин Х и Y (табл. 2):

									Таблица 2
Х	Y	Х	Y	Х	Y	Х	Y	Х		Y
70	66	73	68	59	57	66	61	59		58
66	63	61	60	68	65	74	68	58		57
67	62	74	68	62	60	73	67	70		65
67	63	71	67	69	64	60	58	70		65
77	72	74	72	74	71	68	67	64		60
70	66	65	62	53	56	66	63	68		63
66	63	70	65	63	60	69	66	74		68
64	64	63	60	59	57	73	69	62		59
70	64	68	65	72	70	79	71	60		57
71	66	66	62	64	61	69	69	54		55
65	63	61	59	58	56	63	61	65		63
56	59	70	65	72	69	57	57	71		65
62	59	59	58	63	60	67	62	71		66
70	66	75	69	57	55	58	57	68		67
60	58	73	68	55	55	66	62	56		56
60	59	71	67	74	67	71	66	74		70
76	71	55	58	61	58	67	62	71		68
73	69	62	59	69	65	73	68	59		60
66	62	69	64	58	56	56	54	67		64
65	62	59	61	61	61	69	66	61		59

1. Построить вариационные ряды для величин хi.

Решение. Просматривая выборку из Х, находим минимальное значение х = х1 = 53, которое встречается один раз. Следующее большее значение х2 = 54 встречается также один раз. Продолжая просмотр, получим следующий вариационный ряд для Х:

Таблица 3

хi	53	54	55		56	57		58	59			60	61	62	63	64	65
ni	1	1	2		3	2		4		6		4	5	4	4	3	4

хi	66	67	68		69	70		71	72			73	74	75	76	77	79
ni	7	5	5		6	8		7		2		6	7	1	1	1	1
	Делаем проверку: ∑ni = n = 100 , т.е. вариационный ряд построен, верно.
				(i)
	2. Составляем интервальный ряд распределения для Х.
	По формуле (2.3) найдем длину интервала hх:
					h	=	xmax − xmin		=		79− 53		≈ 3,392
					h	=			=				≈ 3,392
					x	1+ 3,332lgn				1+ 3,332 2			.
						1+ 3,332lgn				1+ 3,332 2

Округляя до ближайшего целого четного числа, получим hx = 4. Находим начало 1-го интервала хнач.:

хнач = хmin – hx/2 = 53 – 2 = 51.

При таком хнач. конец последнего интервала хкон. совпадает с хmах, поэтому в качестве хнач целесообразно взять значение хнач. = 52, чтобы было xmax < xкон..

Заполняем два первых столбца таблицы 4.

					Относительная		Таблица 4
Начало	Конец	Середина		Частота	Относительная		Теоретическая
интервала	интервала xi+ 1		~	~	частота	~	частота
интервала	интервала xi+ 1	интервала хi		интервала ni	частота	~	частота
xi					интервала	pi	интервала nit
52	56		54	5,5	0,055		4,24
56	60		58	15,5	0,155		11,3
60	64		62	16,5	0,165		20,88
64	68		66	20	0,2		25,45
68	72		70	24,5	0,245		20,69
72	76		74	15,5	0,155		11,17
76	80		78	2,5	0,025		4,03
Находим середины интервалов			хi и значения заносим в 3-й столбец таблицы 4.
			~

Из таблицы 3 находим число вариант n~i , попадающих в каждый интервал, и заносим

в4-й столбец таблицы 4.

В5-й столбец таблицы 4 записываем относительные частоты ~рi = n~i / n .

3. Строим гистограмму интервального распределения Х (рис. 7):

На основе гистограммы строим график (сплошная линия) эмпирической функции плотности вероятности Х(fэ(х)), плавно обводя вершины прямоугольников.

~
р
0,25			f(x)
0,2						f*(x)
0,15
0,1
0,05
0							80	x
52	56	60	64	68	72	76	80	x
f*(x) и f(x) – эмпирическая и теоретическая кривые плотности вероятности
		случайной величины Х соответственно
				Рис. 7

4. Из гистограммы видно, что модой является середина 5-го интервала, имеющего

максимальную частоту. Середина 5-го интервала	~	= М0	является модой
максимальную частоту. Середина 5-го интервала	х5 = 70	= М0	является модой
интервального распределения Х.
Срединным интервалом является 4-й интервал,	т.к. середина		этого интервала
~
х4 = 66 = Ме является медианой интервального распределения Х.

5. По формулам (2.5), (2.6), (2.7) соответственно находим среднее х , дисперсию Dx и среднее квадратическое отклонение σх, используя данные таблицы 2:

(53 1

+ K+ 60 4 + K+ 79 1) = 65,97;

х =

∑xi ni =

100

n i=1

{(53− 65,97)2

1}= 34,495;

∑(xi − x)2 ni =

1+K+ (60− 65,97)2

4 +K(79− 65,97)2

100

n i=1

σ x = Dx ≈ 5,873.

По данным таблицы 4 находим выборочное среднее, дисперсию и среднее квадратическое отклонение по формулам (2.8), (2.9), (2.10) соответственно:

m ~ ~

(54

+ 70 24,5 + 74 15,5 + 78 2,5) = 65,96;

хв =

∑xini

5,5 + 58 15,5 + 62 16,5 + 66 20

n i=1

100

{(54 − 65,96)

2,5}≈ 37,92;

1 m ~

Dxв =

∑(xi − xв )

5,5

+ K+

(78 − 65,96)

100

n i=1

σ xв = Dвx ≈ 6,158.

6. Доверительный интервал для оценки математического ожидания находим по формулам (2.13)–(2.16). Из таблицы для Ф (хβ) = 1/2β = 0,45 (приложение 2) находим:

хβ ≈ 1,645.

~	n				100	34,4951 ≈ 34,8435;
Dx =			Dx ≈
Dx =	n − 1		Dx ≈		99
	n − 1		~		99
			~				34,8435 ≈ 0,971;
ε = xβ		Dx		≈ 1,645			34,8435 ≈ 0,971;
			n				100
lβ = (x − ε ; x + ε )= (65,97− 0,971; 65,97+ 0,971)≈ (65; 66,94).

Доверительный интервал для оценки дисперсии находим по формулам (2.17), (2.18):

ε ′ = x β		~	2	≈ 1,645 34,8435	2	≈ 8,1468 ;
ε ′ = x β		D x	~n − 1	≈ 1,645 34,8435	99	≈ 8,1468 ;
	~		~n − 1		99
l′	= (D	− ε ′ ; D + ε )= (34,8435− 8,1468; 4,8435+ 8,1468) ≈ (26,7 ; 43).
β	x		x

7. Используя данные из таблицы 4 и вычисленные значения xв и σхв, по формуле (2.17) вычисляем теоретические частоты для интервала nit:

			56− 65,96		52− 65,96
	= 100					≈ 100 {Ф(−1,617)− Ф(− 2,267)}= 100 {Ф(2,267)− Ф(1,617)}≈
n		Ф		− Ф
			6,158		6,158
1t
				4,24;
≈ 100 (0,4885− 0,0642) ≈

…………………………………………………………………………………………………….

	80	− 65,96		76
					− 65,96	≈ 100 {Ф(2,28)− Ф(1,63)}≈ 100 (0,4887− 0,4484) ≈ 4,03.
n7t = 100 Ф			− Ф
	6,158			6,158

Вычисленные частоты заносим в 6-й столбец таблицы 4.

Значения относительных частот интервалов nit/100 с абсциссами ~хi заносим на рис.6

и через эти точки проводим теоретическую кривую (штриховая линия). Видно, что ход теоретической кривой качественно совпадает с ходом эмпирической кривой.

8. С помощью критерия согласия Пирсона проверяем гипотезу о нормальном распределении Х. Т.к. имеются частоты с малочисленными интервалами (1-й и 7-й), то объединяем 1-й интервал со вторым, а 7-й – с шестым. Заполняем таблицу 5 для новых частот niэ и kit:

Таблица 5

24,5

niэ

16,5

kit

15,54

20,88

25,45

20,69

15,2

По данным таблицы 5 находим χ набл2

. :

χнабл2 . = ∑5

(niэ − kit )2

≈ 5,32.

i =1

kit

Находим число степеней свободы k:

k = l – 3 = 5 – 3 = 2.

Для уровня значимости α = 0,05 и k = 2 из таблицы 5 находим критическое значение

χ кр2

. = 6. Т.к.

χ кр2

. > χ набл2

. (6 >

5,32),

то гипотезу

о нормальном

распределении Х

принимаем.

Аналогичным образом проводим расчеты для выборки Y.

1. Строим вариационный ряд:

Таблица 6

yi	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72
ni	1	3	4	6	6	7	7	5	8	7	5	8	8	6	7	5	2	3	2

2. Составляем интервальный ряд распределения Y.

		hу	=	уmax − уmin			=		72 −	54	≈ 2,35;
Округляя, получим hу = 2.		hу	=	1 + 3,332	2		=	7,664			≈ 2,35;
				1 + 3,332	2			7,664

Начало 1-го интервала:		унач = уmin – hу/2 = 54 – 1 = 53.
		унач = уmin – hу/2 = 54 – 1 = 53.
Заполняем два первых столбца таблицы 7.														Таблица 7
												Относительная		Таблица 7
Начало	Конец		Середина					Частота			~	Относительная		Теоретическая
интервала	интервала уi+1			~							~	частота	~	частота
интервала	интервала уi+1	интервала уi				интервала ni						частота	~	частота
уi												интервала	pi	интервала nit
53	55			54				2,5				0,025		2,63
55	57			56				8,5				0,085		5,57
57	59			58				12,5				0,125		9,67
59	61			60				13				0,13		14,08
61	63			62				14				0,14		16,93
63	65			64				12,5				0,125		16,82
65	67			66				15				0,15		13,93
67	69			68				12,5				0,125		9,53
69	71			70				6				0,06		5,4
71	73			72				3,5				0,035		2,54

Находим середины интервалов и заполняем 3-й столбец таблицы 7.

Используя таблицу 6, заполняем 4-й столбец таблицы 7.	~	~
В 5-й столбец таблицы 7 заносим относительные частоты
	рi	= ni / n .

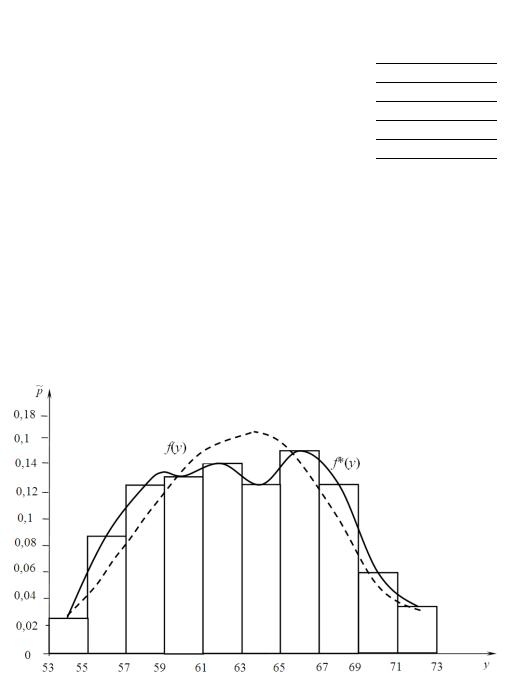
3. Строим гистограмму интервального распределения Y (рис. 8):

f*(у) и f(у) – эмпирическая и теоретическая кривые плотности вероятности случайной величины Y соответственно

Рис. 8

По гистограмме строим график эмпирической функции плотности вероятности

Y(fэ(y)).

4. Из гистограммы видно, что модой является середина 7-го интервала, т.е. ~х5 = 67

можно считать модой М0 интервального распределения Y.

Верхняя граница 5-го интервала является медианой интервального распределения,

т.е. Ме = 63.

5. Находим у , Dу, σу:

(54 1+ 55 3 + K+ 71 3 + 72 2) = 62,96;

у =

∑уini =

100 i=1

100

Dу

∑(уi − у)2 ni ≈ 20,5;

100 i=1

σ у

Dу ≈ 4,53 .

Находим ув , Dув, σув:

1 100

~ ~

ув

∑

уi ni

= 62,96;

100 i=1

1 10

Dув =

∑(уi − ув) ni ≈ 21;

100 i=1

σ ув =

Dув

≈ 4,58.

6. Находим доверительный интервал для оценки математического ожидания:

Ф(уβ) = 1/2β = 0,45; уβ ≈ 1,645.

100

20,5

Dу =

Dу ≈

≈ 20,7;

n −1

20,7

ε = уβ

Dу

≈ 1,645

≈ 0,75;

100

lβ = (у− ε ; у+ ε ) = (62,96− 0,75; 62,96+ 0,75) ≈ (62,21; 63,71).

Находим доверительный интервал для оценки дисперсии:


	~		2	≈ 1,645 20,7		2	≈ 4,84;
ε ′ = уβ Dу			n − 1	≈ 1,645 20,7		99	≈ 4,84;
′	~	′	~	′	− 4,84; 20,7+ 4,84) ≈ (15,86; 25,54.)
lβ = (Dу −ε			; Dу + ε )= (20,7		− 4,84; 20,7+ 4,84) ≈ (15,86; 25,54.)

7. Используя данные из таблицы 6 и вычисленные значения ув и σув, по формуле

(2.17) вычисляем теоретические частоты для интервала nit и заносим в 6-й столбец таблицы 7.

Значения относительных частот интервалов nit/100 с абсциссами ~уi заносим на рис.8

8. С помощью критерия согласия Пирсона проверяем гипотезу о нормальном распределении Y. Т.к. имеются малочисленные интервалы (1, 10-й для эмпирической частоты и 1, 2, 10-й для теоретической частоты), то объединяем 1-й интервал со вторым,

														~′	~′
	а 10-й с 9-ым. Заполняем таблицу 8 для новых частот ni и nit :																			Таблица 8
~														12,5			15		12,5	Таблица 8
~			11			12,5				13		14									9,5
	ni′		11			12,5				13		14									9,5
	n ′
~			8,2			9,67				14,08		16,93		16,82			13,93		9,53		7,94
	it		8,2			9,67				14,08		16,93		16,82			13,93		9,53		7,94
	По данным таблицы 8 находим χ набл2										. :
	χ набл2			8	~′	′	2			;
	χ набл2	. = ∑			(ni	− ni	)	≈ 4,8		;
			i =1			′
			i =1			nit
	Находим число степеней свободы k:
	~′		− 3 = 8		− 3 = 5.
	k = m		− 3 = 8		− 3 = 5.
	Для уровня значимости α = 0,05 и k = 5 из Приложения 3 находим критическое
	значение		χ кр2	. = 11,1; т.к.					χ кр2	. > χ набл2 .	(11,1		> 4,8),		то гипотезу о нормальном
	распределении принимаем.
																				~
	9. Строим корреляционную таблицу (табл. 9). В 1- й столбец таблицы заносим yi , а в
			~
	1-ю строку xi . Для упрощения нахождения величин nxy указываем также начало и конец
	каждого интервала.																			Таблица 9
																				Таблица 9
	Х		54			58			62		66		70			74		78			ny
	Y		52–56			56–60			60–64		64–68		68–72			72–76		76–80
	54		1,5			1														2,5
	53–55
	56		2,5			5,75			0,25											8,5
	55–57
	58		1,25			6,25				5										12,5
	57–59
	60		0,25			2			9,5		1,25									13
	59–61
	62					0,5			1,25		12		0,25							14
	61–63
	64								0,5		5,25		6,75							12,5
	63–65
	66										1		13			1				15
	65–67
	68										0,5		3,25			8,75				12,5
	67–69
	70												1,25			4		0,75		6
	69–71
	72															1,75		1,75		3,5
	71–73
	nx		5,5			15,5			16,5		20		24,5			15,5		2,5			n = 100

Заполнение таблицы начнем с клетки в верхнем левом углу. Просматривая в табл. 2 значения Х, попадающие в 1-й интервал для Х, подсчитываем число значений Y сопутствующих этим значениям Х и попадающих одновременно в 1-й интервал для Y. Варианты, попадающие на границы интервалов, с весом 0,5 учитываем как для рассматриваемого интервала, так и для соседнего. Если в рассматриваемой паре (х, у) и х,

и y попадает на границу своего интервала, то эта пара заносится в соответствующие клетки с весом 0,25.

После заполнения всех клеток делаем проверку:

∑nx = ∑ny = 100 .

10.Заполненные клетки в табл. 9 группируются около главной диагонали. Это говорит о том, что связь между Х и Y можно считать линейной.

В предположении линейной корреляции между Х и Y по формуле (2.21) находим выборочный коэффициент корреляции rв:

	1		~ ~	~ ~		1
rв =		∑	(nxy )l xl yl − nxl yl		=		{54 (54 1,5 + 56 2,5 + 58 1,25 +
		∑
						100 6,158 4,58
	nσ хвσ ув l					100 6,158 4,58

+60 · 0,25) + 58(54 · 1 + 56 ·5,75 + 58 · 6,25 + 60 · 2 + 62 · 0,5) + 62(56 · 0,25 + 58 ·5 + +60 · 9,5 + 62 · 1,25 + 64 · 0,5) + 66(60 · 1,25 + 62 · 12 + 64 · 5,25 + 66 · 1 + 68 · 0,5) +

+70(62 · 0,25 + 64 · 6,75 + 66 · 13 + 68 · 3,25 + 70 · 1,25) + 74(66 · 1 + 68 · 8,75 + +70·4+72 · 1,75) – 100 · 65,96 · 62,96} ≈ 0,934.

11.Выборочные прямые регрессии Y на Х и Х на Y находим соответственно по формулам (2.22) и (2.23):

− y

= r

σ ув

(x − x

)

σ хв

или

ух = 0,695x +17,14 х = 1,439 ух − 24,66;

− х

= r

σ хв

(y − y

)

σ ув

или

хy

= 1,256 y − 13,1 y = 0,796 ху + 10,43 .

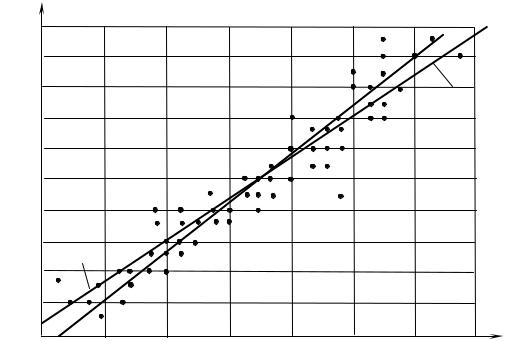
12. На корреляционное поле наносим точки заданной выборки и строим линии регрессии Y на Х и Х на Y (рис. 9).

		у
	73
	71
	69	1
	67	1
	67
	65
	63
	61
	59	2
	57	2
	57
	55
	53

1 – линия регрессии Y на Х; 2 – линия регрессии Х на Y Рис. 9

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

Дана двумерная выборка дискретных случайных величин X = {x1 , x2 ,K, xn } и

Y= {y1, y2 ,K, yn }. Требуется:

1.Построить вариационные ряды для величин xi и yi .

2.Используя вариационные ряды, составить интегральные ряды распределения величин X и Y . Длины интервалов hx и hy найдите по формуле Стерджеса.

3.Построить гистограммы относительных интервальных частот величин X и Y . На основе гистограмм построить графики эмпирических функций плотностей вероятностей величин X и Y .

4.Найти моду и медиану для интервальных распределений X и Y .

5.Используя данные вариационных рядов, найдите статистические средние значения, дисперсии и средние квадратические отклонения X и Y . Используя середины интервалов и частоты интервалов, найти выборочные средние, выборочные дисперсии и выборочные средние квадратические отклонения X и Y . Сделать сравнение вычисленных величин.

6.Найти доверительные интервалы для оценок математического ожидания и дисперсии величин X и Y в предположении о нормальном распределении с доверительной вероятностью β = 0,9 .

7.Считая средние интервальные значения X и Y распределенными по нормальному закону распределения, вычислить для каждого интервала теоретические относительные частоты для X и Y . По найденным частотам построить на одном рисунке с гистограммой графики теоретических функций плотностей вероятностей случайных величин X и Y .

8.В случае качественного совпадения графиков эмпирических и теоретических функций плотностей вероятностей проверить гипотезу о нормальном распределении случайных величин X и Y с помощью критерии Пирсона при уровне значимостиα = 0,05 .

9.Используя интервальные ряды распределения, составить корреляционную таблицу.

10.Найти выборочный коэффициент корреляции в предположении линейной зависимости между X и Y .

11.Найти выборочные уравнения прямой линии регрессии Y на X и прямой линии регрессии X на Y . Построить их на корреляционном поле.

Вариант 1

X	Y	X	Y	X	Y	X	Y	X	Y
72	55	106	79	86	67	89	74	102	76
92	74	90	70	104	77	104	78	112	86
107	79	92	74	74	58	95	79	96	74
81	70	111	83	76	58	114	84	82	62
110	82	94	70	91	68	91	68	81	61
100	77	103	78	91	70	87	66	83	64
95	78	98	75	95	73	87	68	107	79
82	62	93	71	97	74	81	66	98	74
86	70	87	66	98	75	99	75	83	62
96	76	109	83	99	76	113	83	84	67
104	81	91	71	109	81	113	86	89	69
98	75	100	76	105	78	84	65	69	55
97	73	101	80	100	74	101	75	95	71
91	75	88	67	103	79	92	70	103	78

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.2015404.72 Кб293323.pdf
#
09.04.20153.84 Mб143327-p.pdf
#
09.04.2015753.52 Кб483336_EI.pdf
#
15.03.20161.27 Mб113341 ЭИ.pdf
#
09.04.2015546.24 Кб363366.pdf
#
15.03.2016562.2 Кб163392_EI.pdf
#
09.04.2015562.53 Кб723393_EI.pdf
#
15.03.2016529.33 Кб193400.pdf
#
15.03.2016650.93 Кб3843404_EI.pdf
#
15.03.20162.16 Mб193409 ЭИ.pdf
#
15.03.20161.11 Mб503411.pdf

yi	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72
ni	1	3	4	6	6	7	7	5	8	7	5	8	8	6	7	5	2	3	2

X	Y	X	Y	X	Y	X	Y	X	Y
72	55	106	79	86	67	89	74	102	76
92	74	90	70	104	77	104	78	112	86
107	79	92	74	74	58	95	79	96	74
81	70	111	83	76	58	114	84	82	62
110	82	94	70	91	68	91	68	81	61
100	77	103	78	91	70	87	66	83	64
95	78	98	75	95	73	87	68	107	79
82	62	93	71	97	74	81	66	98	74
86	70	87	66	98	75	99	75	83	62
96	76	109	83	99	76	113	83	84	67
104	81	91	71	109	81	113	86	89	69
98	75	100	76	105	78	84	65	69	55
97	73	101	80	100	74	101	75	95	71
91	75	88	67	103	79	92	70	103	78

yi	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72
ni	1	3	4	6	6	7	7	5	8	7	5	8	8	6	7	5	2	3	2

X	Y	X	Y	X	Y	X	Y	X	Y
72	55	106	79	86	67	89	74	102	76
92	74	90	70	104	77	104	78	112	86
107	79	92	74	74	58	95	79	96	74
81	70	111	83	76	58	114	84	82	62
110	82	94	70	91	68	91	68	81	61
100	77	103	78	91	70	87	66	83	64
95	78	98	75	95	73	87	68	107	79
82	62	93	71	97	74	81	66	98	74
86	70	87	66	98	75	99	75	83	62
96	76	109	83	99	76	113	83	84	67
104	81	91	71	109	81	113	86	89	69
98	75	100	76	105	78	84	65	69	55
97	73	101	80	100	74	101	75	95	71
91	75	88	67	103	79	92	70	103	78

yi	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72
ni	1	3	4	6	6	7	7	5	8	7	5	8	8	6	7	5	2	3	2

X	Y	X	Y	X	Y	X	Y	X	Y
72	55	106	79	86	67	89	74	102	76
92	74	90	70	104	77	104	78	112	86
107	79	92	74	74	58	95	79	96	74
81	70	111	83	76	58	114	84	82	62
110	82	94	70	91	68	91	68	81	61
100	77	103	78	91	70	87	66	83	64
95	78	98	75	95	73	87	68	107	79
82	62	93	71	97	74	81	66	98	74
86	70	87	66	98	75	99	75	83	62
96	76	109	83	99	76	113	83	84	67
104	81	91	71	109	81	113	86	89	69
98	75	100	76	105	78	84	65	69	55
97	73	101	80	100	74	101	75	95	71
91	75	88	67	103	79	92	70	103	78