
- •34. Формальные модели для изучения проблемы взаимных блокировок. Обнаружение блокировок при наличии нескольких экземпляров ресурсов каждого типа.
- •35. Безопасное распределение ресурсов на примере алгоритма банкира.
- •36. Управление памятью. Сегментная организация памяти компьютера. Совместное использование памяти. Защита памяти и защищенный режим работы процессора.
- •37. Управление памятью. Страничная организация памяти компьютера.
- •38. Управление памятью. Сегментно-страничная организация памяти компьютера.
- •39. Виртуальная память. Механизм реализации виртуальной памяти. Стратегия подкачки страниц. Программная поддержка сегментной модели памяти компьютера. Основы функционирования менеджера памяти.
- •Общая структура файловой системы
- •41. Управление вводом-выводом в ос. Основные принципы организации ввода-вывода в ос. Режимы управления вводом-выводом в ос. Основные системные таблицы ввода-вывода.
- •42. Проблемы надежности и безопасности ос. Защитные механизмы ос (принципы построения, защита от сбоев и несанкционированного доступа). Идентификация и аутентификация.
- •Идентификация и аутентификация
- •Шифрование паролей в операционных системах
- •Авторизация.
- •Выявление вторжений. Аудит системы защиты
- •Основные защитные механизмы ос семейства Windows
- •43. Авторизация. Разграничение доступа к объектам ос.
- •44. Средства аппаратной поддержки мультипрограммирования на примере процессоров семейства Pentium. Средства аппаратной поддержки сегментно-страничной организации памяти компьютера(доработать)
34. Формальные модели для изучения проблемы взаимных блокировок. Обнаружение блокировок при наличии нескольких экземпляров ресурсов каждого типа.
Взаимная блокировка - ситуация, когда каждый из группы процессов ожидает событие, которое может вызвать только другой процесс из этой группы.
Существует четыре стратегии избегания взаимоблокировок:
1. Пренебрежением проблемой в целом.
2. Обнаружение и устранение (взаимоблокировка происходит, но оперативно ликвидируется).
3. Динамическое избежание тупиков.
4. Предотвращение условий, необходимых для взаимоблокировок.
Если вероятность взаимоблокировки очень мала, то ею легче пренебречь, т.к. код исключения может очень усложнить ОС и привести к большим ошибкам. Также многие взаимоблокировки тяжело обнаружить.
Этот алгоритм используется как в UNIX, так и в Windows.
Система не пытается предотвратить взаимоблокировку, а пытается обнаружить ее и устранить.
Обнаружение взаимоблокировки при наличии нескольких ресурсов каждого типа
Рассмотрим систему.
m - число классов ресурсов (например: принтеры это один класс)
n - количество процессов
P(n) - процессы
E- вектор существующих ресурсов
E(i)- количество ресурсов класса i
A- вектор доступных (свободных) ресурсов
A(i) - количество доступных ресурсов класса i
С- матрица текущего распределения (какому процессу, какие ресурсы принадлежат)
R- матрица запросов (какой процесс, какой ресурс запросил)

C(ij) - количество экземпляров ресурса j, которое занимает процесс P(i).
R(ij) - количество экземпляров ресурса j, которое хочет получить процесс P(i).
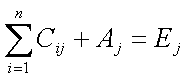
Общее количество ресурсов равно сумме занятых и свободных ресурсов
Рассмотрим алгоритм поиска тупиков.

Алгоритм поиска тупиков при наличии нескольких ресурсов каждого типа
Если остаются не маркированные процессы, значит, есть тупик.
Рассмотрим
работу алгоритма на реальном примере.
Используем алгоритм:
1. Третий процесс может получить желаемые ресурсы, т.к. R (2 1 0 0) = A (2 1 0 0)
2. Третий процесс освобождает ресурсы. Прибавляем их к A. А = (2 1 0 0) + (0 1 2 0) =(2 2 2 0). Маркируем процесс.
3. Может выполняться процесс 2. По окончании А=(4 2 2 1).
4. Теперь может работать первый процесс.
Тупиков не обнаружено.
Если рассмотреть пример, когда второму процессу требуются ресурсы (1 0 3 0), то два процесса окажутся в тупике.
Когда можно искать тупики:
· Когда запрашивается очередной ресурс (очень загружает систему)
· Через какой-то промежуток времени (в интерактивных системах пользователь это ощутит)
· Когда загрузка процессора слишком велика
35. Безопасное распределение ресурсов на примере алгоритма банкира.
Алгоритм банкира (Э. Дейкстра) – алгоритм распределения ресурсов операционной системой, обеспечивающий избежание тупиков. Его условия и принципы: возможны множественные экземпляры ресурсов; каждый процесс должен априорно обозначить свои максимальные потребности в ресурсах; при запросе ресурса возможно ожидание процесса; после получения ресурсов процесс должен вернуть их за ограниченный период времени. Для работы алгоритма используются вектор доступности ресурсов каждого вида, матрица максимальных потребностей процессов, матрица фактического выделения системой ресурсов процессам, матрица оставшихся потребностей процессов в ресурсах.
Структуры данных для алгоритма банкира
Пусть в системе имеется n процессов и m типов ресурсов.
Вектор Available длины m содержит информацию о доступных ресурсах. Если Avaliable[j] = k, то в системе в данный момент доступно k единиц ресурса j.
Матрица Max (n * m) отображает максимальные потребности процессов в ресурсах. Если Max [i, j] = k, то процесс i может запросить, самое большее, k единиц ресурса j.
Матрица Allocation ( n * m ) отображает фактическое выделение системой ресурсов. Если Allocation [i, j] = k, то процессу i в данный момент выделено системой k единиц ресурса j.
Матрица Need ( n * m ) отображает оставшиеся потребности процессов в ресурсах. Если Need [i, j] = k, то процессу i могут потребоваться еще k единиц ресурса j для завершения работы.
Имеет место следующее соотношение между элементами матриц:
Need [i, j] = Max [i, j] – Allocation [i, j].
