Решение.

В точке А балка АВ жестко заделана (связь – жесткая заделка). Такая связь дает множество сил, действующих на заделанный конец балки. Но согласно основной теореме статики произвольная система сил приводится к одной силе (главному вектору) _А и одной паре – главному моменту М_А. Главный вектор заменим его составляющими _А и _А, направленными произвольно по осям Ах и Ау соответственно (рис.16). С учетом этого в заделке имеем две силы реакции _А и _А и момент М_А, направление которого указываем тоже произвольно. В точке В связью является нить, к противоположному концу которой прикреплен груз Q, вес которого задан. Поэтому реакция нити равна силе Q и направлена от точки В по нити. Неизвестными являются силы _А и _А и момент М_А. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси координат равнялись нулю и чтобы сумма моментов всех сил относительно точки А тоже равнялась нулю, то есть

; (8)

;

.

Рис. 16

Из (8) следует

; ;

.

После подстановки в эти уравнения численных значений Р, Q, q, M, , , заданных в условии задачи, получим значения неизвестных:

Х_А=101/2 +51/2=7,5 кН;

Y_А=2 4/2 – 10 /2 – 5/2 = - 8,99 кН;

М_А=216/8 – 10  4/2/2 + 3 – 54/2= -27,6 кНм.

Задача С2. Определение реакций опор и сил в стержнях плоской фермы.

Дано: Р₁ = 20 Н, Р₂ = 10 Н,  = 45⁰ ,  = 45⁰ , а = 1 м.

Определить усилия в стержнях фермы

Рис.17

Решение.

Простая статически определимая ферма (рис.17) составлена из n узлов и s стержней, число которых связано соотношением s = 2n - 3.

Стержень 14 (СА) не принадлежит ферме, но с его помощью ферма крепится к опоре А, то есть для фермы стержень 14 является связью. В точке В ферма связана неподвижным цилиндрическим шарниром с другим телом. Поэтому, освободив ферму от связей, получим свободное твердое тело, на которое действуют активные силы ,и силы реакций связей,,, причемнаправлена вдоль стержня СА, а,- параллельны осям координат (рис.18 и 19). Определим эти неизвестные силы. Для этого, считая ферму абсолютно твердым телом, составим уравнение равновесия для системы сил, приложенных к ферме как для произвольной плоской системы сил:

1) = Х_В – R_A + P₂sin = 0;

2) =Y_B + P₂cos  P₁ = 0; (9)

3) = R_Aa  P₂sina P₁3a + P₂cos 2a = 0

Из третьего уравнения системы (9) найдем

R_A=P₂sin + P₁3  P₂2cos=10/2 +203 102/2 = 53 Н.

Из второго уравнения (9) найдем Y_В

Y_В=Р₂сosP₁=10/2  20 = 12,9 Н.

Из первого уравнения (9) найдем Х_В

Х_В = R_A + P₂sin= 53 + 10/2 = 46 Н.

Усилия в стержнях найдем методом вырезания узлов. Для этого каждый раз будем вырезать тот узел, к которому приложено не более двух неизвестных усилий в стержнях фермы (ферма плоская). Таким узлом является узел В (рис.18). Неизвестными являются усилия R₁, R₄ в первом и четвертом стержнях соответственно. Имеем плоскую систему сходящихся сил. Составим уравнения равновесия:

1) ;

2) .

Рис. 18

Решая эти уравнения относительно R₁ и R₄, получим:

R₁ = Y_B =  12,9 Н;

R₄ = X_B = 46 Н.

Теперь вырежем узел А. К этому углу подходят три стержня – первый, второй и третий (рис. 19). Усилие в первом стержне определено из рассмотрения узла В. Таким образом, неизвестными усилиями являются усилия R₂ и R₃ в стержнях втором и третьем соответственно. Для определения этих неизвестных составим уравнение равновесия как для плоской системы сходящихся сил:

1) ;

2) .

Рис. 19

Откуда получим:

R₃= R₁1/sin = 12,292/2 = 18,4 Н;

R₂= R_A  R₃ cos= 53,0718,4/2 = 40,2 Н.

Вырежем узел III (рис.20). Неизвестными являются усилия R₅ и R₆ в стержнях 5 и 6 соответственно. Уравнения равновесия:

1)  R₂+R₆=0;

2) R₅=0.

Откуда: R₅ = 0, R₆ = R₂ = 40,2 Н.

Рис. 20

Вырежем узел IV. Неизвестными являются усилия R₇ и R₈ (рис. 21) Уравнения равновесия:

1) R₄ R₃cos+R₇cos+R₈=0;

2) R₃sin+R₅+R₇sin=0,

oткуда

R₇= R₃= 18,4 Н;

R₈=2R₃cos+R₄=36,8/2+(46) =  20,02 Н.

Рис. 21

Вырежем узел VI (рис. 22). Неизвестными являются усилия R₉ и R₁₂. Уравнения равновесия

1) R₈+R₁₂=0;

2) R₉=0,

oткуда получаем:

R₉=0;

R₁₂ = R₈ = 20,02 Н.

Рис. 22

Вырежем узел V (рис.23). Неизвестными являются усилия R₁₀ и R₁₁. Уравнения равновесия

1) R₆  R₇cos+R₁₁+R₁₀cos+P₂sin=0;

2) R₇sin  R₉  R₁₀sin+P₂cos=0,

откуда

R₁₀= P₂ R₇= 28,4 Н;

R₁₁=R₆+R₇cos  R₁₀cos P₂sin = 40 Н.

Рис. 23

Усилия в стержне 13 определим, вырезав узел VII (рис.24). Уравнения равновесия

1)  R₁₂ R₁₀cos = 0;

2) R₁₃ + R₁₀sin - Р₁ = 0.

Из второго уравнения получим усилие в стержне 13:

R₁₃= R₁₀sin + Р₁ =28,4/2 + 20 = 0,08 Н.

Рис.24

Из первого уравнения получим тождество, как то и должно быть, то есть

20,02 - 28,4/2=0.

Это свидетельствует о правильности решения.

Указание: при вырезании узлов усилия в стержнях рекомендуется направлять от узла.

Задача С3. Определение реакций опор составной конструкции (система двух тел).

Дано: Р = 100 Н, Q = 30 Н, q = 5 Н/м, M = 10 Нм,  = 90⁰ ,  = 60⁰ ,  = 30⁰.

Определить реакции опор А и В и в шарнире С.

Рис. 25

Решение.

Система состоит из двух балок АС и ВС, соединенных друг с другом внутренней связью (неподвижным цилиндрическим шарниром) в точке С. Один конец балки АС в точке А закреплен с помощью жесткой заделки, а балка ВС в точке В опирается на каток. Поэтому после освобождения системы двух тел в точках А и В от связей получим свободное твердое тело, изображенное на рис. 26, а разделив его в точке С, получим свободное твердое тело, изображенное на рис.27.

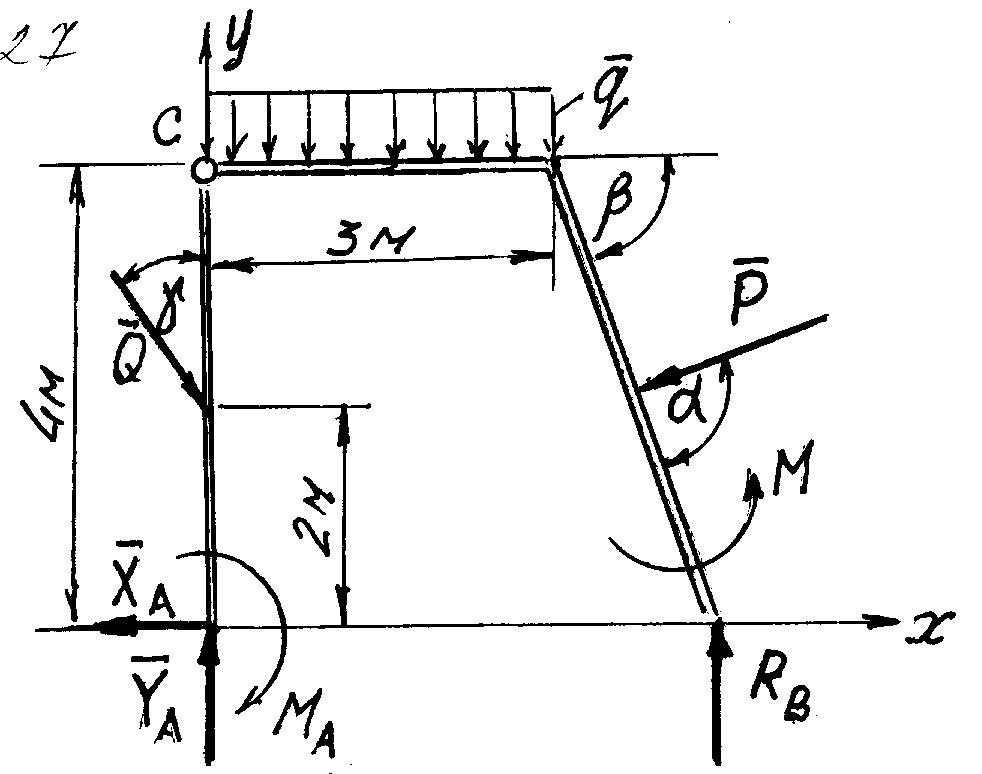
Рис.26 Рис.27

Неизвестными являются силы Х_А, Y_А, R_В, Х_С, Y_С и момент М_А. Всего 6 неизвестных. Следовательно, нужно составить 3 уравнения равновесия произвольной плоской системы сил, изображенной на рис.26 и 3 уравнения для системы рис.27. Получим систему шести алгебраических уравнений относительно шести неизвестных:

1) =Х_А+Qsin Psin=0;

2) =Y_A Qcos q3  Pcos +R_B=0;

3) =Qsin2 M_Aq31,5 + Psin2

 Рcos(3+2ctg)+M+R_B(3+4ctg)=0;

4) =X_A+Qsin+X_C=0;

5) =Y_AQsin+Y_C=0;

6) = X_A4+Qsin2M_A=0.

Из первого уравнения получим Х_А:

Х_А= Рsin + Qsin = 100/2 + 301/2 = -71,6 Н.

Из четвертого уравнения получим Х_С:

Х_С=Х_А Qsin= 71,6  301/2= 86,6 Н.

Из шестого уравнения получим М_А:

М_А= Х_А4+2Qsin = 71,64 +2301/2= 316,4 Нм.

Из третьего уравнения найдем R_В:

R_B=1/(3+4ctg)[2Qsin+M_A+4,5q2Psin+Pcos(3+2ctg)M]== 74 Н.

Из второго уравнения найдем Y_А:

Y_A=Qcos+q3+PcosR_B= 16,9 Н.

Из пятого уравнения найдем Y_С:

Y_С=Qcos  Y_A = 8,9 Н.

Проверка:

= Х_A4  M_A+Qsin23q1,5Psin2 -Pcos(3+2/3)+M+R_B(3+4/3) =

= 403+403 = 0.

Задача С 4. Определение реакций опор твердого тела

Дано: Q = 50 Н, F = 20 Н,  = 60⁰,  = 45⁰, R = 0,5м, r = 0,2 м.

Определить силу Р и реакции подшипников А и В.

Рис. 28

Решение.

Подшипники представляют связь, которая называется неподвижный цилиндрический шарнир с осью, совпадающей с координатной осью Ау. Трение не учитывается. Поэтому силы реакции этих связей представим в виде составляющих, параллельных осям Ах и Аz в точках А и В – это силы ,,,(рис.28). Следовательно, всего неизвестных пять: Р, Х_А, Z_A, X_B, Z_B. Учитывая, что все силы расположены в плоскостях перпендикулярных оси Ау, получим пять уравнений равновесия сил и моментов:

1)= Х_А+Рсos+X_BFcosQcos=0;

2)=Z_APsin+Z_B+Fsin+Qsin=0;

3)=Psin2+Z_B3+Fsin5+Qsin5=0;

4)=Pcosr +FR QR=0;

5)=Pcos2X_B3+Fcos5+Qcos5=0.

Анализируя эти уравнения, видим, что одну неизвестную содержит только четвертое уравнение. Поэтому последовательность решения следующая. Из четвертого уравнения находим Р:

P=(1/(rcos))(QR - FR)=(12/(0,21))(50-20)1/2= 150 Н.

Из пятого уравнения найдем Х_В:

Х_В=(1/3)(2Pcos+5Fcos+5Qcos)=0,33(21500,5+520/2 +5500,5)=15 Н.

Из первого уравнения найдем Х_А:

X_A= Pcos  X_B+Fcos+Qcos= 1500,5  15 +20/2 + 500,5= 51 Н.

Из третьего уравнения найдем Z_B:

Z_B=(1/3)(2Psin5Fsin5Qsin)=(1/3)(2150/2520/2550/2) ==8,9 Н.

Из второго уравнения найдем Z_A:

Z_A=PsinZ_BFsinQsin=150/2 +8,920/2 50/2 = 81,4Н.

Проверка:

= 1500,50,2+200,5500,5 = 0.