
Матан_Дифф_Уравн
.pdf
|
|
|
|
|
32 |
|
|
|
|
|
d 2 x |
= 3 dx |
−2 dy ; |
d 2 x |
= 3 dx |
−2(−x +2y) ; |
|
|
|
|
|
dt2 |
dt |
dt |
dt2 |
dt |
|
|
|
|
|
|
d 2 x |
= 3 dx |
+2x −4y . |
|
|
|
|
|
|
|
|
dt2 |
dt |
|
|
|
|
|
1 |
|
|
dx |
Из первого уравнения системы выразим y : |
y = |
|
3x − |
|||||||
2 |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
dt |
|
Тогда уравнение |
d 2 x |
= 3 dx |
+2x −4y можно переписать в виде |
||||||
|
|
|
|
|
|
dt2 |
|
dt |
|
d 2 x |
= 3 |
dx |
+2x −2 |
|
3x − |
dx |
. Данное уравнение является линейным |
||
dt |
2 |
dt |
|
|
|||||
|
|
|
|
|
dt |
|
|
||
дифференциальным уравнением второго порядка для определения неизвестной функции x(t) . Приводя подобные, запишем его в виде
d 2 x −5 dx + 4x = 0 . dt2 dt
Составим характеристическое уравнение и найдем его корни:
λ2 −5λ +4 = 0 ; (λ −1)(λ −4) = 0; λ1 =1,λ2 = 4 .
Решение дифференциального уравнения имеет вид |
|
|
||||||||||||||||
x = C1et +C2e4t , где C1,C2 - произвольные постоянные. |
|
|
||||||||||||||||
Найдем y(t) . Так как y = |
1 |
3x − dx |
, то, подставляя x = C et +C |
e4t , |
||||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
1 |
2 |
|
|
получаем: |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = |
1 |
|
− |
|
1 |
(3C1e |
t |
+3C2e |
4t |
−C1e |
t |
−4C2e |
4t |
); |
|
|
||
2 |
3x |
dt |
= |
2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y = C1et − |
1 C2e4t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда общее решение системы имеет вид:
x = C1et +C2e4t ;
y = C1et − 12 C2e4t .
Где C1,C2 - произвольные постоянные.
Используя начальные условия, найдем произвольные постоянные. Так как x(0) =1, y(0) =1, то для определения C1,C2 имеем систему
уравнений:
C1 +C2 =1;
C1 − 1 C2 =1.2
Решая систему, получаем С1 =1,C2 = 0. Ответ: x = et ,
y = et .
32
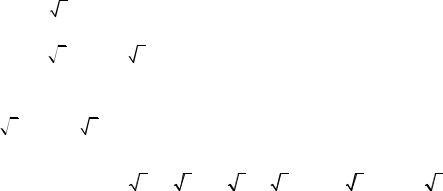
33
Задача 25. Найти общее решение системы дифференциальных уравнений
dxdt = x +4y,
dy = x − y.dt
Продифференцируем первое уравнение. Получаем
d 2 x = dx +4 dy . dt2 dt dt
Подставим в полученное уравнение значение dydt , взятое из второго уравнения системы. Получаем
d 2 x |
= dx |
+4(x − y) ; |
|
|
|
|
dt2 |
dt |
|
|
|
|
|
d 2 x |
= dx |
+4x −4y . |
|
|
|
|
dt2 |
dt |
|
|
1 |
dx |
|
Из первого уравнения системы выразим y : |
y = |
|
||||
4 |
|
− x . |
||||
|
|
|
|
dt |
|
|
Тогда уравнение |
d 2 x |
= dx |
+4x −4y можно переписать в виде |
|||||
|
|
|
|
|
dt2 |
dt |
|
|
d 2 x |
= |
dx |
dx |
− x |
|
. Данное уравнение является линейным |
||
dt |
2 |
dt |
+4x − |
|
||||
|
|
dt |
|
|
|
|
||
дифференциальным уравнением второго порядка для определения неизвестной функции x(t) . Приводя подобные, запишем его в виде
d 2 x +5x = 0 . dt2
Составим характеристическое уравнение и найдем его корни:
λ2 +5 = 0 ; λ = ±
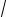 5i .
5i .
Решение дифференциального уравнения имеет вид
x = C1 sin 
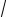 5t +C2 cos
5t +C2 cos 
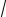 5t , где C1,C2 - произвольные постоянные.
5t , где C1,C2 - произвольные постоянные.
Найдем |
y(t) . Так как |
y = |
1 |
dx |
|
, то, подставляя |
4 |
|
− x |
||||
|
|
|
dt |
|
|
x = C1 sin 
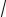 5t +C2 cos
5t +C2 cos 
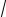 5t , получаем:
5t , получаем:
|
1 |
dx |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
= |
(C1 |
5 cos 5t −C2 |
5 sin 5t −C1 sin 5t −C2 cos 5t ); |
|||||||||||||||
4 |
|
− x |
4 |
||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
33

34
y = C1 14 (
 5 cos
5 cos 
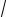 5t −sin
5t −sin 
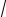 5t )+C2 14 (−
5t )+C2 14 (−
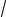 5 sin
5 sin 
 5t −cos
5t −cos 
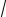 5t ).
5t ).
Тогда общее решение системы имеет вид:
x = C1 sin 
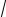 5t +C2 cos
5t +C2 cos 
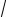 5t ;
5t ;
y = C1 14 (
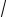 5 cos
5 cos 
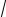 5t −sin
5t −sin 
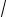 5t )+C2 14 (−
5t )+C2 14 (−
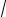 5 sin
5 sin 
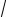 5t −cos
5t −cos 
 5t ).
5t ).
Где C1,C2 - произвольные постоянные.
Ответ: x = C1 sin 
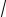 5t +C2 cos
5t +C2 cos 
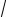 5t ;
5t ;
y = C1 14 (
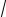 5 cos
5 cos 
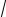 5t −sin
5t −sin 
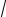 5t )+C2 14 (−
5t )+C2 14 (−
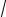 5 sin
5 sin 
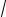 5t −cos
5t −cos 
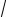 5t ).
5t ).
Задача 26. Найти общее решение системы дифференциальных уравнений
dxdt = x +4y,
dy = 2x +3y.dt
Продифференцируем первое уравнение. Получаем
d 2 x = dx +4 dy . dt2 dt dt
Подставим в полученное уравнение значение dydt , взятое из второго уравнения системы. Получаем
d 2 x |
= dx |
+4 dy ; |
d 2 x = dx +4(2x +3y) ; |
|
|
|
|
||||
dt2 |
|
dt |
dt |
dt2 |
dt |
|
|
|
|
||
d 2 x |
= dx |
+8x +12y . |
|
|
|
|
|
|
|||
dt2 |
|
dt |
|
|
|
|
|
1 |
dx |
|
|
Из первого уравнения системы выразим y : |
y = |
|
|||||||||
4 |
|
− x . |
|||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
Тогда уравнение |
d 2 x |
= dx +8x +12y можно переписать в виде |
|||||||||
|
|
|
|
|
|
dt2 |
dt |
|
|
|
|
d 2 x |
= |
dx |
+8x +3 |
dx |
− x |
|
|
|
|
|
|
dt |
2 |
dt |
|
. Данное уравнение является линейным |
|||||||
|
|
|
dt |
|
|
|
|
|
|
||
дифференциальным уравнением второго порядка для определения неизвестной функции x(t) . Приводя подобные, запишем его в виде
d 2 x −4 dx −5x = 0 . dt2 dt
34
35
Составим характеристическое уравнение и найдем его корни:
λ2 −4λ −5 = 0 ; (λ +1)(λ −5) = 0 ; λ1 = −1,λ2 = 5 .
Решение дифференциального уравнения имеет вид |
|
|
|
|
|
|
|||||||||||||||
x = C1e−t +C2e5t , где C1,C2 |
- произвольные постоянные. |
|
|
|
|||||||||||||||||
Найдем y(t) . Так как y = 1 dx |
− x , то, подставляя |
x = C e−t +C |
2 |
e5t , |
|||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
получаем: |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y = |
1 |
|
1 |
(−C1e |
−t |
+C2 5e |
5t |
−C1e |
−t |
−C2e |
5t |
)= − |
1 |
C1e |
−t |
+C2e |
5t |
. |
|||
4 |
|
− x = |
4 |
|
|
|
|
2 |
|
|
|
||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда общее решение системы имеет вид:
x = C1e−t +C2e5t ;
y = − 12 C1e−t +C2e5t .
Где C1,C2 - произвольные постоянные.
Ответ: x = C1e−t +C2e5t ;
y = − 12 C1e−t +C2e5t .
35
36
4.Пример решения варианта типового расчета
Задача 26. Найти общий интеграл дифференциального уравнения y′ = x2e−y 1.
Данное уравнение является уравнением с разделяющимися переменными
Тогда f (x) = x21−1 , g(y) = ey . Заметим, что g(y) ≠ 0. Разделяем переменные:
e−y dy = x2dx−1.
Интегрируя правую и левую части, получаем
∫e−y dy = ∫x2dx−1 .
После вычисления интегралов имеем: −e−y = 12 ln xx +−11 +C . Ответ: −e−y − 12 ln xx +−11 = C .
Задача 27. .Найти общий интеграл дифференциального уравнения
y′ = yy +− xx + xy .
Данное уравнение является однородным. Будем искать неизвестную функцию y(x) в виде y = xu . Тогда Подставляя y и y′в исходное уравнение, получаем:
u + x dudx = uu +−11 +u .
Полученное уравнение преобразуем к виду
dudx = 1x uu +−11 .
Разделяем переменные
(u +1) du = dx . |
|
(u −1) |
x |
Интегрируем правую и левую части

37
∫((uu +−1)1) du = ∫dxx +ln C .
(В нашем случае произвольную постоянную удобнее обозначит не С, а ln C , где C ≠ 0. Вычисляя интегралы в правой и левой
частях уравнения, получаем
u + 2ln u −1 = ln x +lnC .
Потенцируя, имеем
eu (u −1)2 = Cx .
Избавляясь от знака модуля, получаем eu (u −1)2 = Cx .
Поскольку u = xy , то полученное соотношение может быть представлено в виде
|
y |
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ex |
|
|
−1 = Cx . |
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Данное выражение преобразуем к виду |
|
|
|
||||||||||
e |
y |
(y − x)2 = Cx3 |
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
||||||
Заметим, что в уравнении |
du |
= |
1 u −1 |
, выражение |
u −1 |
= 0 |
|||||||
|
|
|
|
|
|
|
|
dx |
|
x u +1 |
|
u +1 |
|
при u1 =1. Следовательно, функция u =1 является решением дифференциального уравнения для неизвестной функции u(x), а значит, функция y = x является решением исходного
дифференциального уравнения.
y
Решение y = x содержится в решении e x (y − x)2 = Cx3 , если
положить С=0.
y
Ответ: e x (y − x)2 = Cx3 , где С – произвольная постоянная.
Задача 28. Найти решение дифференциального уравнения y′+(tgx)y = 2xcos x ,
удовлетворяющее начальному условию y(0)=1.
Вначале найдем общее решение этого уравнения. Будем искать y в виде y = uv . Тогда y′=u′v +uv′. Подставляя y и y′ в
38
исходное уравнение, получаем: u′v +uv′+(tgx)uv = 2xcos x;
(v′+vtgx)u +u′v = 2xcos x .
Выберем функцию v(x) из условия v′+vtgx = 0. Уравнение для функции v(x) является уравнением с разделяющимися
переменными. Найдем его решение: v′+vtgx = 0, dvv = −tgxdx;
∫dvv = −∫tgxdx; ln v = ln cos x ; v = cos x .
Найдем функцию u(x): u′cos x = 2xcos x; u′ = 2x ; u = ∫2xdx; u = x2 +C .
Тогда общее решение исходного уравнения имеет вид y = uv = (x2 +C)cos x .
Произвольную постоянную С определим из условия y(0) =1:
1 = C .
Ответ: y = (x2 +1)cos x.
Задача 29..Найти решение дифференциального уравнения
′ |
3 |
−2x |
|
2 |
|
|
y + y = |
2 e |
|
y |
|
, |
удовлетворяющее начальному условию |
y(0)=2. |
|
|
|
|
|
|
Данное уравнение является уравнением Бернулли. Будем искать y в виде y = uv . Тогда, подставляя y и y′в исходное
|
|
|
|
|
′ |
|
|
|
′ |
3 |
|
−2x |
2 |
|
2 |
:. Функцию v(x) |
|||||||
уравнение, получим u v +u(v |
|
+v) = 2 e |
|
u |
v |
|
|||||||||||||||||
определяем из условия: |
dv |
+v = 0; dv |
= −dx; |
∫dv |
= −∫dx; |
||||||||||||||||||
|
|
|
|
|
|
dx |
|
|
|
v |
|
|
|
3 |
|
|
v |
|
|
|
|
||
ln v = −x ; v = e |
−x |
|
|
|
|
|
′ |
|
−x |
|
|
−2x |
2 |
|
−2x |
|
|||||||
|
. Определим u(x): u e |
= |
2 e |
|
|
u |
e |
|
; |
||||||||||||||
du 3 |
−3x |
|
du 3 |
|
−3x |
|
1 |
|
1 |
|
|
−3x |
|
|
|
|
|||||||
u2 = |
2 e |
|
dx; |
∫u2 = |
2 ∫e |
|
|
dx+С; −u = − |
2 e |
|
|
+C ; |
|
||||||||||
u = − |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 e−3x +C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39
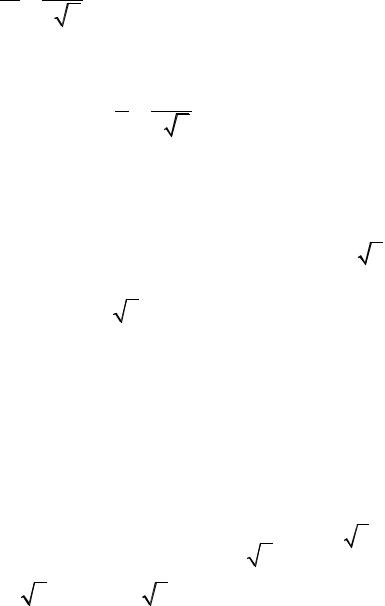
Следовательно, общее решение имеет вид y = − |
|
e−x |
|||||
|
|
. Из |
|||||
− |
1 e−3x +C |
||||||
|
|
|
|
|
|
2 |
|
условия |
|
y(0) = 2 определяем произвольную постоянную С: |
|||||
2 = − |
|
1 |
; С=0. |
|
|
|
|
− |
1 |
+C |
|
|
|
||
|
|
|
|
|
|||
|
|
2 |
y = 2e2x . |
|
|
|
|
Ответ: |
|
|
|
||||
Задача 30..Найти общее решение дифференциального уравнения y′′+ yx′ = 4 9x .
Это уравнение явно не содержит y . Обозначим y′ = z . Тогда: y′′ = z′. Подставляя в исходное уравнение, получаем
z′+ xz = 4 9x .
Уравнение для определения функции z(x) линейным дифференциальным уравнением первого порядка. Будем искать
z в виде z = uv. Тогда |
z |
′ |
=u v +uv |
. Подставляя z |
|
и z |
′ |
в |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′ |
|
|
|
uv |
= |
9 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||
исходное уравнение, получаем: |
u v +uv |
+ |
|
4 x |
; |
|
|
|
||||||||||||||||||||||||||||
(v |
′ |
|
|
v |
|
′ |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
+ x)u +u v = 4 |
|
x . |
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Выберем функцию v(x) из условия v′+ |
= 0. Уравнение для |
|||||||||||||||||||||||||||||||||||
x |
|
|||||||||||||||||||||||||||||||||||
функции v(x) является уравнением с разделяющимися |
|
|
|
|||||||||||||||||||||||||||||||||
переменными. Найдем его решение: v′+ |
v |
|
0, |
dv |
|
|
dx |
|
||||||||||||||||||||||||||||
|
= |
v = − |
x |
; |
||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||
∫dv |
= −∫dx ; ln v = −ln x; v = |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
v |
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
9 |
|
|
|
; u′ = |
9 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Найдем функцию u(x): u′ x |
= |
|
|
|
|
4 |
|
x ; |
|
|
|
|
|
||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|||||||||||||||||||||||||||||
u = 9 |
|
|
3 x |
|
+C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
xdx ; u = |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
4 ∫ |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

40
Тогда для функции
z = uv = 3 x
2
Так как y′ = z , то
z(x) имеем выражение
|
+C |
1 |
= 3 |
|
+ C1 . |
x |
x |
||||
1 |
|
2 |
|
x |
|
|
|
x |
|
||
y = |
∫ |
zdx +C |
|
|
∫ |
|
3 |
|
+ C1 dx +C |
|
= x |
|
+C ln x |
+C ., где |
||||||||||||||
|
= |
x |
|
x |
||||||||||||||||||||||||
|
|
2 |
|
|
2 |
|
x |
|
2 |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
C1,C2 - произвольные постоянные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Задача 31. Найти решение дифференциального уравнения |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
4y3 y′′ = y4 −1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяющее начальным условиям y(0)= 2 , y |
(0)= 2 2 . |
|||||||||||||||||||||||||||
Так как исходное уравнение явно не содержит независимую |
||||||||||||||||||||||||||||
переменную x |
, будем искать y |
′ |
в виде |
y |
′ |
= p(y) . Тогда |
y |
′′ |
= p p . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
||||||
Подставляя y′′ |
и y′ |
в исходное уравнение, получаем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4y3 p dpdy = y4 −1.
Полученное для p(y) уравнение является уравнением с разделяющимися переменными. Найдем его решение:
|
dp |
|
|
|
|
|
y4 −1 |
, 4 pdp = |
y4 −1 |
dy , 4∫pdp = ∫ |
y4 −1 |
|
|
|
||||||||||||||||||||||||
4 p dy |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy , |
|
|
||||||||||||||||||
|
|
|
|
y3 |
|
|
y3 |
|
|
|
y3 |
|
|
|
|
|||||||||||||||||||||||
2 p |
2 |
= |
y2 |
|
+ |
1 |
|
|
|
+C . Определим произвольную постоянную С. |
||||||||||||||||||||||||||||
|
2 |
|
|
|
2y |
2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как при x = 0 имеем y(0) = |
|
|
′ |
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
2 |
|
|
|
, то |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
, а y (0) = 2 |
2 |
|
|
|
||||||||||||||||||||||||||||||||||
p = |
|
1 |
|
|
|
|
при y = |
|
|
. Тогда |
1 |
=1+ 1 +C , С=−1. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
= y2 + |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|||||||
Следовательно, |
|
|
−2 = |
y − |
|
или |
p |
= |
|
y − |
. |
|||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|
|
|
|
y |
|||||
Знак плюс при извлечении корня выбран потому, что

41
′ |
|
1 |
|
|
- положительное число. Неизвестную функцию |
|
|
|
|
||
y (0) = 2 |
2 |
|
|||
|
1 |
|
|
|
y(x) определяем из уравнения y′ = y − |
|
. Найдем его |
||
|
||||
|
y |
|
||
|
|
dy |
|
1 |
|
ydy |
= dx , |
|
ydy |
|
|
dx , |
||||||
решение: |
|
= y − |
|
|
, |
|
|
|
|
|
|
|
= |
|
||||
dx |
|
(y |
2 |
−1) |
∫(y |
2 |
−1) |
∫ |
||||||||||
1 ln(y2 |
|
|
y |
|
|
|
|
|
|
|
||||||||
−1) = x +C . Так как y(0) = |
|
, то 0 = 0 +C , C = 0. |
||||||||||||||||
2 |
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, ln(y2 −1) = 2x , y = 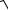
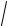 1+e2x .
1+e2x .
|
|
|
|
|
|
|
|
|
|
|
Ответ: y = |
1+e2x . |
|||||
Задача |
|
32. |
Найти |
решение дифференциального уравнения |
||||
|
′′ |
|
′ |
|
|
e−x |
|
|
y |
+3y |
+ 2y = 2 +ex |
, удовлетворяющее начальным условиям |
|||||
|
|
|||||||
y(0)= 0, y′(0)= 0 .
Найдем решение однородного уравнения. Составляем характеристическое уравнение: λ2 + 3λ + 2 = 0 . Найдем его корни: λ1 = −2,λ2 = −1. Однородное уравнение имеет два
линейно независимых решения y1 = e−2x и y2 = e−x . Частное
решение y ищем в виде
y = C1(x)e−2x +C2 (x)e−x , где функции C1(x) и C2 (x) удовлетворяют системе уравнений:
C1′e−2x +C2′e−x = 0, −2C1′e−2x −C2′e−x = 2e+−xex .
Решая систему, получаем: C1′ = −2 +exex , C2′ = (2 +1ex ) . Находим C1 и C2 : C1 = −∫2e+xdxex , C2 = ∫(2 dx+ex ) . Для вычисления первого интеграла сделаем замену переменной
