
- •5. Понятие инвестиционного портфеля. Ожидаемая доходность и риск портфеля.
- •1.2. Ожидаемая доходность портфеля.
- •8. Теорема разделения.
- •9. Индексная модель и capm модель.
- •10. Оценка систематического и несистематического рисков отдельного актива и портфеля.
- •11. Диверсификация. Хорошо диверсифицированный портфель.
- •12. Основные допущения сарм. Модель сарм и ее применения.
- •14. Критика сарм.
- •15. Оценка уровня управления портфелем: показатели Шарпа, Трейнора.
- •16. «Альфа» Дженсена.
- •17. Определение ценности облигации и портфеля облигаций. Доходность к погашению облигации.
- •18. Временная структура процентных ставок. Кривая доходностей.
- •19. Дюрация облигации и портфеля облигаций, как мера риска.
- •20. Кривизна облигации и портфеля облигаций.
- •21. Иммунизация , как стратегия оптимизации владельцем облигаций принимаемого риска.
- •22. Иммунизация рисков долговых обязательств с помощью приобретения портфеля облигаций.
15. Оценка уровня управления портфелем: показатели Шарпа, Трейнора.
Показатели доходности и риска представляют собой результаты деятельности менеджера по управлению портфелем. Если сравнивать портфели только на основе их абсолютных значений, то, как правило, сложно получить какую-либо значимую картину. Например, доходность одного портфеля за год составила 50%, а второго — 70%. Результаты управления вторым портфелем кажутся более предпочтительными. Однако, если его риск был в два раза больше риска первого портфеля, то более успешным оказался первый менеджер. Поэтому для оценки эффективности управления портфелем используются относительные показатели, учитывающие как доходность, так и риск портфеля. Показатели эффективности управления портфелем имеют одинаковую структуру. В числителе стоит превышение доходности портфеля над ставкой без риска (rр - rf), поскольку именно данная величина должна выступить в качестве премии за риск портфеля. В знаменателе ставится показатель риска, который может быть или величиной бета, или стандартным отклонением, или (для портфеля облигаций) относительной дюрацией. Первый показатель называют ко-эффициентом Шарпа. Он равен:
![]()
где: rP — средняя доходность портфеля за рассматриваемый период;
rf — средняя ставка без риска за данный период, обычно она рассматривается как средняя геометрическая;
σр — стандартное отклонение доходности портфеля.
Коэффициент Шарпа учитывает доходность портфеля, полученную сверх ставки без риска, и весь риск, как систематический, так и не систематический.
Второй показатель — это коэффициент Трейнора. Он равен:
![]()
В отличии от коэффициента Шарпа в качестве меры риска в нем учитывается бета портфеля.
Третий показатель — коэффициент эффективности для портфеля облигаций. В качестве меры риска используется относительная дюрация. Он равен:
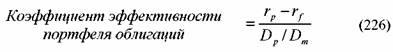
![]() —
отношение дюрации портфеля
облигаций к дюрации
—
отношение дюрации портфеля
облигаций к дюрации
рыночного портфеля облигаций.
Коэффициент Шарпа в качестве риска учитывает стандартное отклонение. Поэтому его следует использовать инвестору, портфель которого не является широко диверсифицированным. Коэффициент Трейнора лучше применять лицам с широко диверсифицированным портфелем, поскольку мерой риска здесь выступает величина бета.
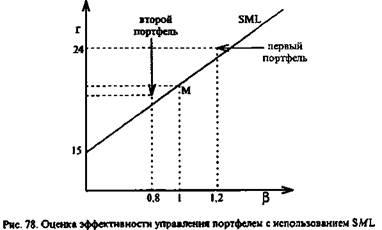
Определяя эффективность управления портфелем, инвестор, как правило, должен сделать два сравнения. Первое заключается в определении наилучшего портфеля среди нескольких данных портфелей. Второе — в сравнении активно управляемого портфеля с результата-ми рынка, т. е. с аналогичным по степени риска пассивным портфелем. Если портфели сопоставляются с использованием одного из приведенных выше показателей, то, чем выше его значение, тем лучше результаты управления. Например, средняя ставка без риска за некоторый период равна 15%, средняя доходность первого портфеля 24%, второго — 21%. Бета первого портфеля — 1, 2, второго — 0, 8. Тогда коэффициент Трейнора первого портфеля равен:
 образом,
с точки зрения эффективности управления,
данные портфели оказались одинаковыми,
т. е. на единицу риска менеджер получил
7, 5 единиц вознаграждения.
образом,
с точки зрения эффективности управления,
данные портфели оказались одинаковыми,
т. е. на единицу риска менеджер получил
7, 5 единиц вознаграждения.
Допустим теперь, что фактическая SML имеет следующее уравнение:
 2,
т. е. доходность портфеля, расположенного
на SML, составила:
2,
т. е. доходность портфеля, расположенного
на SML, составила:
Для второго портфеля, расположенного на SML (с бетой 0, 8), коэффициент Трейнора также равен 7. Таким образом, в рассмотренном случае активные стратегии позволили получить более высокую доходность по сравнению с доходностью рынка. Можно предположить, поскольку показатели Трейнора для портфелей были выше чем для рынка, менеджеры, видимо, получили более высокую доходность за счет правильно выбранного времени покупки и/или продажи активов.
Сравнить портфели друг с другом можно и графически, как показано на рис. 78. Здесь представлена фактическая SML, на которой располагаются пассивные портфели. Если сравниваемый портфель находится ниже SML, то это означает, что менеджер получил результат хуже рыночного. Если же портфели расположены выше SML, то активное управление принесло более высокую доходность чем рынок.
Допустим теперь, что стандартное отклонение первого портфеля составило 30%, второго — 15%, а рынка — 20%. Тогда коэффициент Шарпа для первого портфеля равен:
 эффективные
портфели должны располагаться на CML.
Уравнение CML имеет вид:
эффективные
портфели должны располагаться на CML.
Уравнение CML имеет вид:

Если оценивать результаты управления портфелем с использованием коэффициент Шарпа, то получается, что для первого портфеля он равен 0, 3, в то время как для портфеля на CML, т. е. портфеля с аналогичным уровнем общего риска — 0, 35. Поэтому можно сделать вывод: менеджер данного портфеля оказался не очень опытным в выборе конкретных активов, включил в портфель активы с большим не-рыночным риском и не получил за него адекватного вознаграждения.

Коэффициент Шарпа для второго портфеля равен 0, 4, в то время как для портфеля на CML — только 0, 35. Это означает: второй менеджер показал умение в выборе конкретных активов, т. е. он включил в портфель активы с более высоким нерыночным риском, но и получил соответственно более высокую компенсацию. Результаты управления портфелями можно сравнить наглядно, как показано на рис. 79.
Выше мы отметили, что согласно коэффициенту Шарпа первый менеджер оказался менее опытным в выборе активов чем второй. В то же время в оценке деятельности по управлению портфелем не следует исключать и фактор возможной удачи. Чтобы судить более объективно о навыках управляющего, необходимом рассмотреть его результаты за относительно длительный период, как минимум несколько лет.
Таким образом, сравнивая коэффициенты Трейнора и Шарпа, можно получить различные результаты оценки управления портфелем относительно результатов рынка. Данное отличие возникает в связи с тем, что портфели могут содержать различную степень специфического риска даже при одинаковых значениях беты или иметь различную бету при одинаковых стандартных отклонениях.
Оценка портфелей на основе значения альфы
Оценить эффективность управления портфелем можно на основе определения величины его альфы. В зависимости от степени диверсификации портфеля, а также его вида (т. е. акций или облигаций) следует определить альфу или на основе уравнения SML или CML для акций или облигаций. Чем выше окажется значение альфы, тем лучше результативность менеджера. Для определения альфы на основе SML вначале определяется ожидаемая доходность портфеля соответствующего уровня риска с помощью SМL:
 :
rр — фактическая доходность портфеля,
:
rр — фактическая доходность портфеля,
ΑР — альфа, рассчитанная на основе SML.
Альфу, полученную на основе SML, называют индексом Дженсена (Jensen differential performаnсе nwdex). Величину αp можно представить графически как показано на рис. 80. rp — это фактическая доходность портфеля, a SML — это ожидаемая линия рынка актива. Индекс Дженсена может служить для оценки результатов как активной, так и пассивной стратегии.

Менеджер, следующий пассивной стратегии, не ставит пере собой задачу получить более высокую доходность, чем доходность рынка. Поэтому он ориентируется на результаты, представленные для портфелей, расположенных на ожидаемой SML. Если фактическая альфа оказывается не равной нулю, это говорит о том, что менеджер недостаточно опытен в прогнозировании будущей конъюнктуры рынка.
Как мы уже отмечали, САРМ является моделью одного временного периода, для которого существует одно значение rf и Е(rm). Если рассматривать более продолжительный период (период Т, состоящий из нескольких отрезков времени ti, то для каждого периода t будут меняться и ожидания конъюнктуры. Поэтому для каждого следующего временного периода пассивный менеджер должен строить новую SML с новыми значениями rf и Е(rт). Однако на основе значений rf и Е(rт) для каждого отрезка времени ti можно рассчитать ожидаемую SML для периода Т, для которой rf и Е(rт) — это средние значения ставки без риска и ожидаемой доходности рынка для периодов ti. В результате получим ожидаемую SML на основе средних значений:
![]()
![]() —
ожидаемая доходность портфеля
в конце периода Т;
—
ожидаемая доходность портфеля
в конце периода Т;
![]() — средняя ставка без риска;
— средняя ставка без риска;
![]() — средняя ожидаемая доходность
рынка.
— средняя ожидаемая доходность
рынка.
Таким образом, αр, полученная как отклонение реальной доходности портфеля от ожидаемой SML, покажет умение пассивного менеджера предвидеть будущую конъюнктуру.
В отношении активного менеджера положительная альфа в рамках одного периода t (т. е. в рамках модели одного периода, когда конъюнктура не меняется) будет говорить о его умении выбрать недооцененные активы. Для длительного периода Т (состоящего из отдельных периодов t) положительная альфа может явиться результатом как умелого выбора конкретных активов, так и времени их покупки и/или продажи, т. е. фиксации рынка.
Показатель α для облигаций определяется на основе SML для облигаций с использованием относительной дюрации в качестве значения беты.
Показатель ασ на основе стандартного отклонения определяется путем определения ожидаемой доходности с использованием ожидаемой CML и уравнения:
![]()
