2.4. Эффективная ставка

Формула сложных процентов (2.10) включает четыре неизвестных S(0),S(t),r,t. Зная три неизвестных из уравнения (2.10) можно определить четвертое неизвестное. Сама формула сложных процентов (2.10) определяет будущий капиталS(t) через настоящий капиталS(0), процентную ставкуrи времяt.

В примере 11находится времяtнакопления капитала при известных значениях настоящегоS(0) и будущего капиталаS(t) и процентной ставкиr. В предыдущем разделе, посвященном дисконтированию, в формуле (2.23) современное значениеS(0) капитала определяется по его будущему значениюS(t), процентной ставкеrи времениt. Из формулы сложных процентов (2.10) не определялась только процентная ставкаrчерез настоящийS(0) и будущийS(t) капитал и времяt. Решение этой задачи связано с очень важным экономическим понятием эффективной ставки.

Для сравнения различных вариантов сделок удобно использовать эффективную ставку .

Эффективнойназывают годичную ставкусложных процентов, обеспечивающую заданное отношение полученной суммыS(t) к выданной суммеS(0), независимо от того, какая схема оплат используется в данной конкретной сделке.

Из (2.10) имеем уравнение для определения :

,

где t– длительность сделки в годах.

Тогда:

. (2.26)

Очевидно, что эффективная ставка не зависит от объемов конкретных сумм S(0) иS(t), а определяется только отношениями этих сумм.

Пример 21.

Найти эффективную ставку сделки, в результате которой первоначальный капитал утроился за 5 лет.

Согласно (2.26) имеем .

Пример 22. Удвоение ВВП.

Найти ежегодный темп роста ВВП, при котором он удвоится за 10 лет, за 7 лет, за 3 года.

Решение:

Воспользовавшись формулой эффективной ставки (2.26):

,

получим ежегодный темп роста ВВП, соответственно, для 10 лет, 7 лет и

3-х лет

Пример 23.

В долг дана сумма 2 млн руб. с условием возврата через 2,5 года 3 млн руб. Тогда эффективная ставка в данный сделке равна:

.

Пример 24.

Выдан кредит в 2 млн руб. на 3 месяца под 100 % годовых. Найти эффективную ставку.

Учитывая, что кредит краткосрочный, сумма, выплачиваемая через 3 месяца, будет равна:

млн руб.

тогда эффективная ставка будет равна:

, где S(0)=2 млн руб., S(t)=2,5 млн руб., года.

.

Пример 25.

Вексель выдан на сумму 50 млн руб. и содержит обязательство выплатить владельцу эту сумму через 4 месяца. Владелец предъявил банку вексель досрочно. Банк согласился учесть вексель, но с дисконтом 24 % годовых. Найти эффективную ставку.

Решение:

Полученная сумма будет равна:

млн руб.

Тогда эффективная ставка будет равна:

, где S(0)=46 млн руб., S(t)=50 млн руб., года.

.

Пример 26.

Вексель 3 млн руб. выдан на 2 года с годовой учетной ставкой 10 % с дисконтированием 2 раза в год. Найти эффективную ставку. По формуле (2.24) найдем исходную сумму, выплаченную по векселю:

.

Тогда . Следовательно, для эффективной ставки имеем:

.

Пример 27.

Остров Манхеттен был продан в 1624 г. за $24. В 1976 г. его стоимость была $4010⁹. Какова эффективная ставка сделки?

Решение:

В данной задаче интуиция обманывает человека: кажется, что эффективная процентная ставка будет очень большой. Однако расчет по формуле (2.26) даёт следующее значение:

.

Решающим фактором, приводящим к столь скромному значению эффективной процентной ставки, является время. Длительность сделки велика ‑ 352 года.

В ряде случаев для сравнения различных вариантов сделок вместо эффективной ставки используется процентная спот-ставкаr_s. Она определяется аналогично эффективной ставки, только вместо сложных процентов используются непрерывные проценты.

Процентной спот-ставкой называют годичную ставкуr_sнепрерывных процентов, обеспечивающую заданное отношение полученной суммыS(t) к выданной суммеS(0), независимо от того, какая схема оплат используется в данной конкретной сделке.

Из (2.12) имеем уравнение для определения r_s:

,

где t– длительность сделки в годах.

Тогда, после логарифмирования имеем:

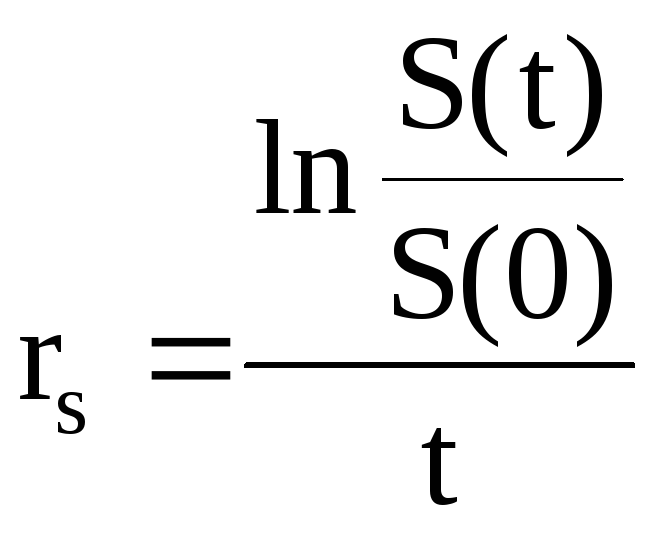. (2.27)

Очевидно, что спот-ставка не зависит от объемов конкретных сумм S(0) иS(t), а определяется только отношениями этих сумм.

Спот-ставка всегда меньше эффективной ставки сделки.

Задача 11.

Для примеров 21-27 найти спот-ставки r_s.

Ответы:

Пример 21. r_s == 21,972%;

Пример 22.r_s ==6,931%,r_s ==9,902%,r_s ==23,105%;

Пример 23.r_s ==16,219%;

Пример 24.r_s ==89,257%;

Пример 25.r_s =3ln=25,014%;

Пример 26.r_s =-2ln0,95=10,259%;

Пример 27.r_s =6,032%;