Ковариация

Пусть x, y– две случайные величины. Оценкаковариации имеет вид:

(П.9)

или (П.10)

Вычислять ковариацию удобнее по формуле:

(П.11)

Оценка ковариации (П.9), (П.11) смещенная, точнее имеет место . Отсюда следует, что несмещенная оценка для ковариации получится при замене в формулах (П.9), (П.11) множителя 1/n на 1/(n-1) т. е.

(П.12)

Размерность ковариации равна произведению размерностей случайных величин xиy.Коэффициентом корреляцииназывается безразмерная величина равная:

(П.13)

где

;

;

.

Коэффициент корреляции изменяется в пределах от -1 до 1:.

При расчете коэффициента корреляции могут быть использованы смещенные и несмещенные оценки, при этом коэффициент корреляции не изменится.

1) Свойства ковариации:

1.

2. , гдеk- постоянный коэффициент;

3. , гдеc– постоянная;

2) Свойства коэффициента корреляции:

1. , гдеc– постоянная;

2. , гдеc– постоянная;

3. при β>0при β<0.

Следовательно:

1.

2.

3. .

Не вдаваясь в тонкости математической статистики можно утверждать, что чем больше длина выборки, тем точнее определяются параметры. Если число параметров и объем выборки сравним, то параметры определить невозможно. Если длина выборки в 1,5÷2-10 раз больше числа параметров, то они определяются достаточно точно.

Линейная регрессия. Парная линейная регрессия

Пусть имеются две случайные величины XиY. Можно ли считать их линейно связанными, т. е. можно лиYсчитать линейной функцией отX? Каковы коэффициенты в этой линейной функции?

Сначала будем считать, что математические ожидания x иyравны нулю, ◦т. е.:

(П.14)

Это не очень большое ограничение, так как в случае отличия от нуля математических ожиданий и, всегда можно перейти к центрированным случайным величинам, . Для них математическое ожидание будет равно нулю.

Найдем коэффициент m, обеспечивающий наилучшую линейную связь междуyиx:

y=mּx(П.15)

Коэффициент m можно выбрать так, чтобы дисперсия разности (невязки)

(П.16)

была минимальной.

Таким образом, mвыбирается из минимума функции

(П.17)

Задача нахождения m, обеспечивающегоminфункции (П.17), типичной задачейметода наименьших квадратов.Для её решения распишем функцию (П.17)

где - дисперсияx,

- дисперсия y,

- ковариация xиy,

- коэффициент корреляции между xиy.

Коротко имеем:

(П.18)

Для нахождения mминимизирующего функцию Φ(m) приравняем к нулю производную:

отсюда (П.19)

Таким образом, уравнение линейной регрессии для случайных величин с нулевым математическим ожиданием имеет вид:

(П.20)

В общем случае при замене x,yнаx-,y-имеем:

,

После элементарных преобразований уравнения линейной регрессии может быть записано в виде:

(П.21)

где ; (П.22)

- математические ожидания x,y;

- дисперсия x,y;

- коэффициент корреляции между xиy.

Погрешность определения линейной регрессии определяется дисперсией невязки:

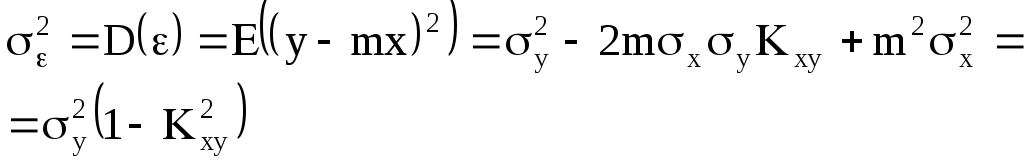(П.23)

Удобно использовать относительное значение дисперсии:

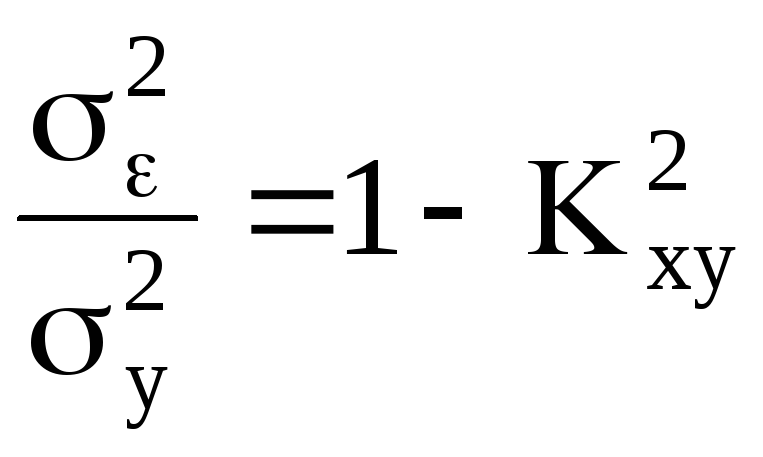(П.24)

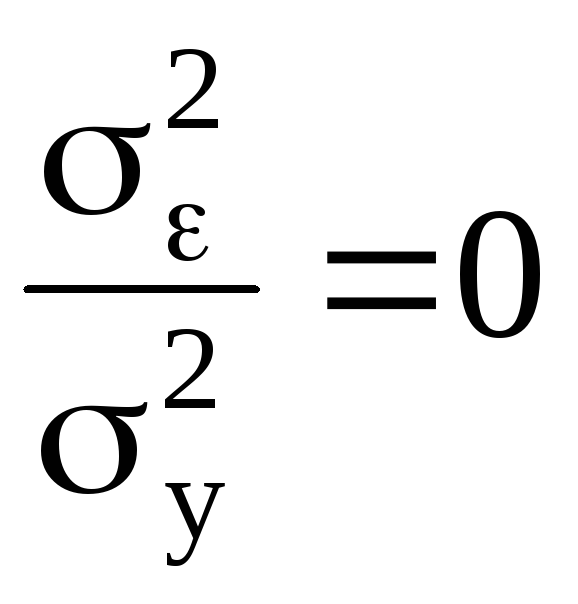Качество линейной регрессии тем лучше, чем ближе к нулю величина . При коэффициенте корреляцииполучими тогда междуyиx имеется точная линейная связь.