4.3.Эффективная ставка, внутренняя эффективность, внутренняя норма доходности (internal rate of return, irr)
Для оценки эффективности инвестиционного проекта, заданного двусторонним потоком платежей, используется понятие эффективной ставки IRR (внутренней эффективности, внутренней нормы доходности (internal rate of return, IRR)).
Чистое современное значение NPV зависит от процентной ставки rи времениt, то есть NPV = NPV( r,t). Если зафиксировать время действия инвестиционного проектаt, то чистое современное значение NPV(r) будет зависеть только от процентной ставки r.
Под эффективной ставкойIRRфинансовой операции понимается значение ставки процентаr, при котором чистое приведенное современное значение (NPV) равно нулю, то есть:
NPV(r) = 0 (4.4)
Таким образом, из (4.1) эффективная ставка является решением уравнения:
(4.5)
где с1, с2,, сn– известные величины платежей со знаками плюс или минус, производимых в моментыt1,t2,,tn.
В общем случае уравнение (4.5) аналитически решить невозможно. Однако в этом случае могут быть использованы хорошо разработанные численные методы, например, метод Ньютона. Эти методы реализованы, например, в «Пакете анализа» в Excel. Название функции вычисляющей эффективную ставкуIRR(чистый внутренний доход).
ЧИСТВНДОХ (значения, даты, начальное значение IRR.(по умолчанию IRR =0,1)).
Найти эффективную ставку IRRможно и графически. Действительно, построим график зависимости чистого современного значения NPV(r) от ставки r (см. рис.4.2.). Это будет монотонно убывающая функция, Точка, в которой график пересекается с осьюrи будет значением внутренней эффективности IRR. Для графика на рис 4.2. эффективная ставка равна 10,5 %.
Экономический смысл эффективной ставки IRR(внутренней нормы доходности) следующий:
Если эффективная ставка IRRравна ставке дисконтирования r (IRR=r), то инвестиционные вложения в точности окупаются доходами, но не приносят прибыли. В этом случае NPV=0.
Если эффективная ставка IRRменьше ставки дисконтирования r, (IRR<r), то инвестиционные вложения не окупаются доходами, а инвестиционный проекта убыточен. В этом случае NPV<0.
Если эффективная ставка IRRбольше ставки дисконтирования r, (IRR>r), то доходы больше инвестиционных вложений, а инвестиционный проект прибыльный. В этом случае NPV>0.
Если проект финансируется за счет коммерческого банка, то значение эффективной ставки IRRпоказывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которой делает проект убыточным.
4.4.Срок (время) окупаемости инвестиционного проекта (discount payback period, dpp)
Чистое современное значение NPV зависит от процентной ставки rи времениt, то есть NPV = NPV( r,t). Если зафиксировать процентную ставку r, то чистое современное значение NPV(t) будет зависеть только от времениtдействия инвестиционного проекта.
В общем случае классического инвестиционного проекта, эта зависимость будет иметь вид. Сначала, при малых значениях времени t, чистое современное значение NPV(t) будет отрицательно. Затем, монотонно возрастая, функция NPV(t) пересекает ось времениtи меняет знак с минуса (-) на плюс (+). Время в инвестиционном проекте меняется дискретно. В связи с этим естественно ввести понятие времени окупаемости следующим образом.
Временем окупаемости инвестиционного проекта называется момент времени, при котором чистое современное значение NPV(t) поменяет знак с минуса (-) на плюс(+).
Сроком окупаемости инвестиционного проекта (discount payback period, DPP) называется промежуток времени от момента начала инвестиционного проекта до момента времени, при котором чистое современное значение NPV(t) поменяет знак с минуса (-) на плюс(+).
Экономический смысл срока окупаемости – это время, необходимое для полной компенсации инвестиций в проект доходами от проекта.
Пример54.
Инвестиционный проект задан двусторонним потоком платежей. Соответствующий поток приведен в двух первых столбцах таблицы 4.1. Процентная ставка равна 10 %. В третьем столбце и на рис 4.3 представлена зависимость чистого современного значения NPV(t) от времени t.
Таблица 4.1.
Расчет чистого современного значения NPV и эффективной ставки IRR для инвестиционного проекта
-
процентная ставка r=
10,00%
Даты
Значения (млн. руб.)
NPV (млн. руб.)
IRR
01.01.2008
-100
-100,00
01.01.2009
-150
-236,33
01.01.2010
0
-236,33
01.01.2011
60
-191,26
-45,78%
01.01.2012
60
-150,29
-22,34%
01.01.2013
60
-113,05
-9,15%
01.01.2014
60
-79,20
-1,04%
01.01.2015
60
-48,43
4,26%
01.01.2016
60
-20,45
7,89%
01.01.2017
60
4,97
10,46%
01.01.2018
60
28,09
12,32%
01.01.2019
60
49,10
13,71%
01.01.2020
60
68,20
14,75%
Чистое современное значение NPV(t) поменяет знак с минуса (-) на плюс (+) в момент времени 01.01.2017. Это и будет моментом окупаемости. Таким образом, срок окупаемости 9 лет.
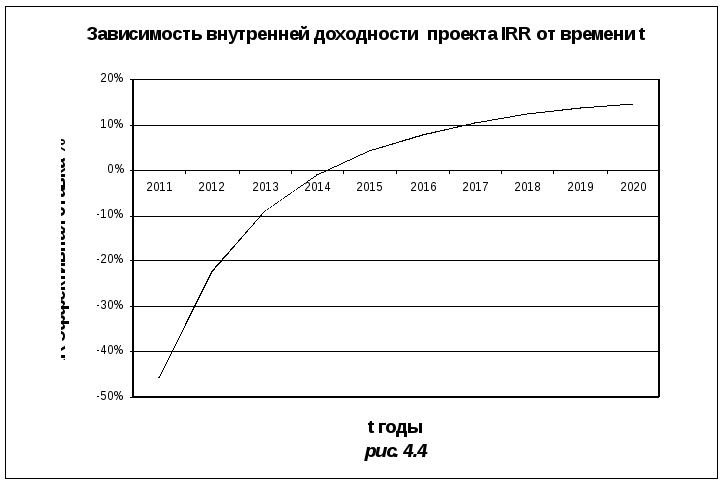
На рис 4.4 и в четвертом столбце таблицы представлена зависимость эффективной ставки IRRот времениt. В момент времени 01.01.2017 она составляетIRR=10,46 %. Это значение превышает процентную ставкуr=10 %, что соответствует времени окупаемости инвестиционного проекта. На рис.4.2. представлена зависимость чистого современного значения NPV(r) от процентной ставкаr(при сроке окончания проекта 01.01.2017). Пересечение графика с осью ОХ соответствует эффективной ставкеIRR=10,46 %.