2.5. Непрерывная ставка (сила роста) и непрерывный дисконт

Дискретная процентная ставка – это ставка, при которой процент начисляется за заранее установленные, или определенные, периоды. Если уменьшить период начисления процентов до бесконечно малой величины (период, за который будут произведены начисления, стремится к нулю, а количество начислений процентов – к бесконечности), то проценты будут начисляться непрерывно. В этом случае процентная ставка называется непрерывной ставкой или силой роста.

В теоретических исследованиях и на практике, когда платежи производятся многократно, удобно использовать непрерывный способ начисления процентов. Переход к пределу может быть осуществлен аналогично тому, как это делалось в пункте 2.2 при выводе формулы (2.12) или следующим способом.

Непрерывная ставка может быть постоянной или изменяющейся. Рассмотрим случай, когда непрерывная процентная ставка в разные моменты времени различна.

Пусть, а(t) – функция, описывающая зависимость непрерывной ставки (силы роста) от времениt. Приращение капиталаS(t) в моментtза промежуток времени Δtравно:

S(t + Δt) – S(t) = a(t) Δt S(t)

Тогда, имеем:

При Δt→0 получим, что скорость изменения капитала пропорциональна капиталу. Тогда, сумма платежа (капитал)S(t) удовлетворяет линейному однородному дифференциальному уравнению первого порядка:

, (2.28)

где

–скорость изменения платежа (скорость изменения капитала);

S(t) - сумма платежа (капитал);

a(t)– непрерывный процент начисления или сила роста.

В другом виде уравнение запишется:

dS=a(t)Sdt, (2.29)

т. е. приращение платежа пропорционально самому платежу Sи приращению времениdt. Коэффициент пропорциональностиа(t) суть сила роста или процент начисления.

Возможна еще одна запись дифференциального уравнения:

, (2.30)

т. е. относительное приращение суммы платежа dS/Sпропорционально приращению времениdt. Причем по-прежнему,а(t)определяется процентами начисления и в общем случае может зависеть от времени. Все три уравнения для капитала (2.28), (2.29), (2.30) эквивалентны.

Рассмотрим некоторые простейшие свойства капитала, описываемого дифференциальным уравнением (2.28)-(2.30). Если функция a(t)>0 положительна, то при положительном капиталеS>0 производная от капиталаdS/dt>0 также положительна и, следовательно, капиталS(t) растет. В этом случаеa(t)называетсянепрерывным процентом начисления или силой роста.

В противном случае если функция a(t)<0 отрицательна, то при положительном капиталеS>0 производная от капиталаdS/dt<0 отрицательна и, следовательно, капиталS(t) убывает. В этом случае абсолютная величина |a(t)|называетсянепрерывным дисконтом.

Решение линейного дифференциального уравнения хорошо известно. Действительно, уравнение (2.30) является уравнением с разделяющимися переменными и его можно проинтегрировать:

Вычислив интеграл, получим:

,

где - неопределенный интеграл отa(t),

С₁- произвольная постоянная.

Отсюда, имеем:

Окончательно, общее решение дифференциального уравнения запишется в виде:

, (2.31)

где - новая произвольная постоянная.

Для определения произвольной постоянной Снужно знать капитал хотя бы в один какой-нибудь момент времени. Если известно что в момент времениt=t₀капитал равенS=S₀(т. е.S(t₀)=S₀), то произвольная постояннаяСлегко определяется из (2.31):

,

или

Подставляя полученный результат в (2.31), имеем:

.

Воспользовавшись классической формулой связи определенного и неопределенного интеграла (формулой Ньютона – Лейбница):

,

получим решение дифференциального уравнения с начальными условиями S(t₀)=S₀ в виде:

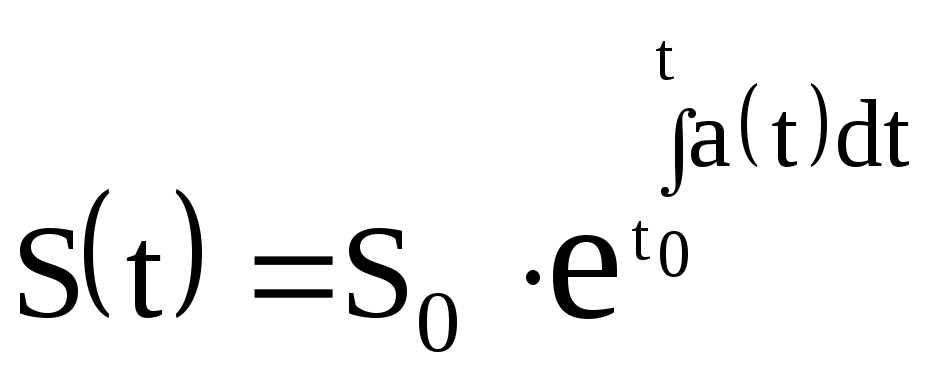
Часто отсчет времени можно производить от начального момент, тогда t₀=0 и решение линейного дифференциального уравнения записывается в виде:

, (2.32)

где

S(0) – начальная сумма в момент 0;

S(t) – сумма платежа в моментt.

Очевидно, приведенные формулы при a(t)>0 соответствуют расчету кредитования, а приa(t)<0 – расчету дисконтирования.

Если сила роста постоянна на всем рассматриваемом промежутке времени, т. е. a(t)=r, то для конечного платежа в моментtимеем:

. (2.33)

Очевидно, эта формула совпадает с полученной ранее предельным переходом формулы для непрерывных процентов (2.12).

Рассмотрим некоторые примеры использования данных формул.

Пример 28.

Ссуда 200 тыс. руб. дана на 2,5 года под ставку 20 % годовых с ежеквартальным начислением. Найти сумму конечного платежа. Расчет произвести по дискретным и непрерывным процентам.

Решение.

Сумма конечного платежа удовлетворяет дифференциальному уравнению , гдеr=20 %=0,2 в соответствии с процентом ежегодного начисления и времяtизмеряется в годах. Решение линейного уравнения известно:

.

Тогда сумма конечного платежа равна:

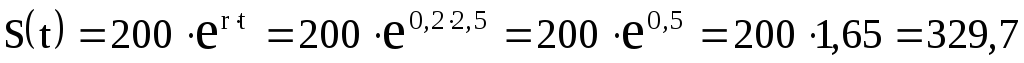тыс. руб.

Расчет для дискретного случая по формулам (2.11) дает:

тыс. руб.

Видно, что при многократных начислениях небольших процентов результаты расчетов сумм конечного платежа близки.

Рассмотрим теперь пример расчета дисконтирования в непрерывном случае.

Пример 29.

Вексель на 3 млн руб. с годовой учетной ставкой 10 % и дисконтированием 2 раза в год выдан на 2 года. Найти исходную сумму, которая должна быть выдана в долг под этот вексель. Расчет произвести по дискретным и непрерывным процентам.

Решение.

Одолженная под вексель сумма платежа удовлетворяет линейному дифференциальному уравнению, решение которого известно:

.

Тогда:

млн руб.

Расчет одолженной под вексель суммы по дискретным формулам (2.24) дает близкие результаты:

млн руб.

Таким образом, теоретические и практические вычисления по непрерывным формулам дают результаты, близкие к результатам расчета по дискретным формулам, если количество начислений велико, а процент начисления невелик.

Применение формулы непрерывного дисконта при оценке инфляции

Инфляции на капитал действует непрерывно, каждую наносекунду, и её влияние будет описываться дифференциальным уравнением вида:

, (2.34)

где – скорость изменения (убывания) капитала;S(t) – капитал;

a(t)– непрерывный дисконт (уровень инфляции).

Из (2.34) при инфляции a(t)>0 и капиталеS>0 производная от капиталаdS/dt< 0 отрицательна и, следовательно, капиталS(t) убывает. После интегрирования дифференциального уравнения (2.34) имеем для зависимости капитала от времени действия инфляции:

(2.35)

где S(0) – начальная сумма в момент 0;

S(t) –конечная сумма в моментt;

- определенный интеграл от инфляции a(t).

Пример 30.

В начале года у господина А имеется 100 тысяч рублей. Какова реальная стоимость этой суммы в конце года, если господинА держит деньги в «чулке»? Под какой процент должны быть вложены деньги, чтобы они не обесценились? Рассмотреть случаи, когда:

1. Инфляция меняется по линейному закону: в начале года она составляет 21 %, а в конце года 9 %.

2. Инфляция меняется по параболическому закону: в начале года она составляет 21 %, а в конце года 9 %. Парабола имеет максимум в начале года при t=0.

3. Инфляция меняется по параболическому закону: в начале года она составляет 21 %, а в конце года 9 %. Парабола имеет минимум в конце года при t=1.

Решение.

Легко видеть (см. рис 2.3), что формулы, описывающие зависимость инфляции (непрерывного дисконта) от времени имеют соответственно вид:

1. a(t) = -12 t+21; 2. a(t) = -12 t²+21; 3. a(t) = 12 (t-1)²+9 (%/год).

Воспользуемся формулой (2.35) для оценки капитала в конце года, для этого сначала нужно вычислить интегралы A(t). Для случаев 1, 2, 3 имеем соответственно:

1. ;

2. ;

3. .

Для определения капитала в конце года нужно в формулу (2.35) и полученные интегралы подставить t=1 год. Тогда, получим:

1. А(1)=15 %, 2. А(1)=17 %, 3. А(1)=13 %.

Полученные значения имеют экономический смысл. Это среднегодовая инфляция. Для линейного закона изменения инфляции она равна 15 % (случай 1), для параболических законов изменения инфляции она равна соответственно 17 % (случай 2) и 13 % (случай 3).

Чтобы деньги не обесценились, они должны быть вложены под процент, превышающий среднегодовую инфляцию.

Найдем теперь реальную стоимость суммы в конце года с учетом инфляции. Из (2.34) при t=1 получим соответственно:

1. S(1) = S(0) e ^{- 0,15} = 100* 0,86071=86,071 тыс. руб.;

2. S(1) = S(0) e ^{- 0,17} = 100* 0,84366=84,366 тыс. руб.;

3. S(1) = S(0) e ^{- 0,13} = 100* 0,87809=87,809 тыс. руб.

При малых значениях процентной ставки возможен упрощенный расчет с использованием замечательного предела . Приблизительное значение суммы в конце года равно соответственно 85 тыс. руб., 83 тыс. руб. и 87 тыс. руб. Очевидно, эти значения близки к суммам, посчитанным по точным формулам.