П.4. Подход различных авторов к формуле Шеннона

Интересно и поучительно проследить, как различные авторы подходили к знаменитой формуле Шеннона.

К. Шеннон (в 1940 г.) пишет ([46], с. 446):

«Если сигнал имеет мощность P, то сигнал, изменённый наложенной помехой, будет иметь мощность P + N. Число хорошо различимых значений есть

, (*)

где K – небольшая константа порядка единицы, зависящая от того, как истолковывается термин “хорошо различимый”».

Затем, при вычислении пропускной способности канала передачи двоичных цифр ([46], с. 448-449), коэффициент K «по умолчанию» приравнивается Шенноном к единице. Доказательство формулы (*) не очень убедительное, поскольку оно основано на теореме Котельникова-Шеннона, которая относится не к сигналам с ограниченной мощностью P, а к сигналам с ограниченной энергией: .

В 1949 г. В. Таллер в статье [57] рассмотрел передачу информации при наличии шума и пришёл к выводу ([57], с. 69):

«Пусть S будет среднее квадратичное значение наибольшего сигнала, который может быть получен в данной системе связи. Предположим, что близко к действительности, что изменение амплитуды сигнала, меньшее, чем амплитуда шума, не может быть обнаружено, но что изменение амплитуды [курсив Таллера – Г. Х.], равное шуму, уже обнаруживается.

Тогда, если N есть среднее квадратичное значение шума, смешанного с сигналом, то имеется 1 + S/N определяющих значений сигнала. Этим определяется s в выражении (1*)…». То есть H = k log s, где k – коэффициент пропорциональности ([57], с. 62), по поводу которого автор статьи ничего не говорит в её тексте; однако из аннотации к статье [57] следует, что k = 1.

В работе [10] 1948 г. Н. Винер, решая задачу оптимальной фильтрации стационарного случайного сигнала ξ(t) на фоне шума n(t) по критерию минимальной дисперсии отклонения выходного колебания оптимального стационарного линейного фильтра от сигнала на его входе (критерий Р. Фишера – [10], с. 153), для распределения по спектру максимального значения отношения «сигнал/шум» получает выражение Q(ω) = [W_ξ(ω) + W_n(ω)]/W_n(ω), где W_ξ(ω) и W_n(ω) – спектральные плотности мощности стационарного сигнала ξ(t) и шума n(t) соответственно.

А поскольку Винер, по совету Дж. фон Неймана, ввёл информационную меру количества информации, связанную с плотностью вероятности p(x), не по Фишеру, а соотношением +log p(x) dx, то при гауссовских стационарных сигналах ξ(t) и помехах n(t) для скорости передачи информации он получает формулу (3.922), в которой нужно считать показатели степени не двойками, а единицами, и которая эквивалентна выражению:

C = .

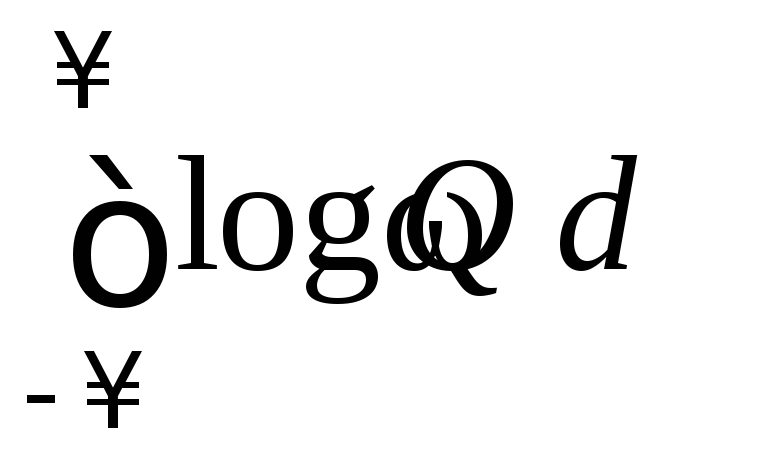Н. Винер добавляет ([10], с. 153):

«Именно этот результат и был получен автором [то есть Н. Винером – Г. Х.] и Шенноном …»

Если W_ξ(ω) = P, W_n(ω) = N, а канал передачи имеет верхнюю частоту среза W, то C = W log , что действительно соответствует формуле Шеннона 1940 г.

В 1948 г. К. Шеннон ([46], с. 243-332) возвращается к формуле (*) уже «во-оружённый» понятиями энтропии дискретных и «непрерывных» сообщений (с. 308):

«Т е о р е м а 17. Пропускная способность канала с полосой частот W, в котором имеется белый тепловой шум мощности N, при условии, что средняя мощность передаваемых сигналов ограничена величиной P, равна

C = W log».

Поскольку максимальный темп передачи сигналов соответствует интервалу Найквиста Δt = 1/(2 W ), это значит, что количество «чётко различимых уровней» есть .

Гауссовские «непрерывные сигналы» и «помехи» соответствуют формуле Шеннона: H(Q) = log = log .

Доказательство теоремы 17, так же как и некоторых других, не очень убедительно. А. Н. Колмогоров по поводу доказательств Шенноном своих теорем заметил ([46], с. 14):

«При необычайном богатстве идей, данных в работах самого Шеннона, изложение в них обычно крайне туманно».