Многопозиционная фазовая манипуляция

При модуляции N-PSK величина равнаU ², а N = 2 π /Δφ, где Δφ – угловое расстояние между соседними позициями созвездия N-PSK. Пропускная спо-

собность C_ц(Q) = 2 F_Н log N₀ определяется, согласно предложенной в разд. 12 методике, величиной Δφ, при которой sin (Δφ/2) = r/U. Отсюда Δφ = 2 arcsin (r/U). А поскольку отношение сигнал/помеха Q есть: Q = 2 U ²/r ², то окончательно получаем: C(Q) = 2 F_Н ;N₀(Q) = .

При r/U =1: Q = 2; N₀(2) = 2; C(2) = 1, что соответствует двухпозиционной фазовой манипуляции 0º/180º. При r/U =1/:Q = 4; N₀(4) = 4; C(4) = 2.

Асимптотически (при Q → ∞): C_ц(Q) = 2 F_Н ;N₀(Q) = . По сравнению с формулой ШеннонаC(Q) ≈ 2 F_Н модуляцияN-PSK

позволяет получить асимптотически на ≈ 1,15 (бит/знак) бóльшую пропускную способность в цифровых каналов радиосвязи с модуляциейN-PSK, чем в аналоговых.

Результаты расчётов зависимостей C_ц(Q) = 2 F_Н ;N₀(Q) = показаны на рис. 31 и 32 кривыми 1.

Квадратурная амплитудная модуляция

При квадратном созвездии модуляции N-QAM (см. [29, 35]):

≡P_кв(M ) = ,

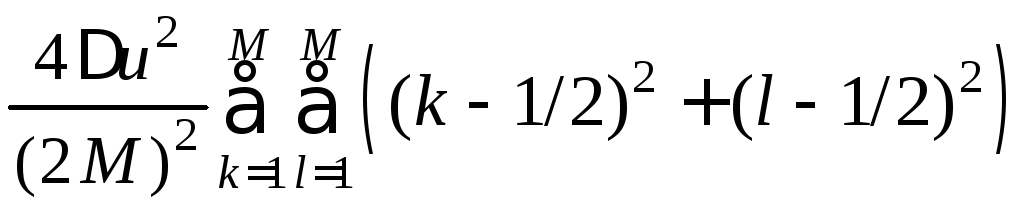или P_кв(M ) = 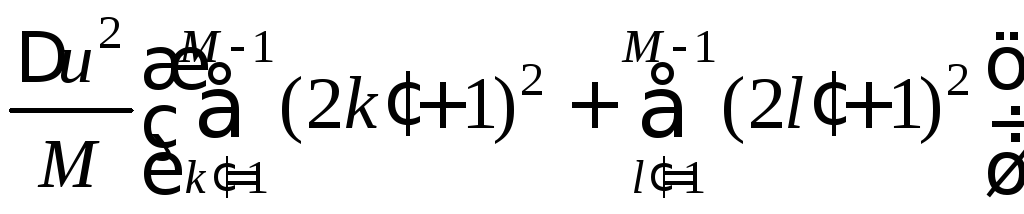= Δu² (2 M – 1) (2 M + 1)/6, (18.1)

где U₀ – диагональ квадрата созвездия N-QAM; Δu – расстояние между соседними позициями по горизонтали или по вертикали; .

Но ; значит,P_кв(M ) = .

Например, при M = 1 (четырёхпозиционная фазовая манипуляция 4-PSK ) P_кв(M ) = P_кв(1) = 3U₀²/3 = U₀², что очевидно.

При M → ∞: P_кв(M ) = P_кв(∞) = U₀²/3, что соответствует дисперсии равномерного распределения случайной величины на квадрате с диагональю 2 U₀.

Таким образом, при модуляции N-QAM с квадратным созвездием отношение сигнал/помеха есть: Q = Δu² (2 M – 1) (2 M + 1)/(3 r ²). Величина пропускной способности C_ц соответствует величине Δu = 2 r ; отсюда получаем:

Q = 4 (2 M + 1) (2 M – 1)/3 = 4 (N₀² – 1)/3; N₀ = 1 + 3 Q/4; C_ц = 2 F_Н log (1 + 3 Q/4).

Результаты расчётов зависимостей C_ц(Q) = 2 F_Н log (1 + 3 Q/4) и N₀(Q) = = 1 + 3 Q/4 показаны на рис. 31 и 32 кривыми 2.

бит С_ц

знак

3

7

6

5 ШЦ 2

4

1

3

Ш

2

1

0

1 3 10 30 100 300 Q

Рис. 31. Сравнительная оценка пропускной способности

современных цифровых каналов радиосвязи

При гексагональном созвездии модуляции N-QAM величина N приобретает следующий ряд значений: N = 6, 18, 36, 60, 90, 128 и т. д. Поэтому при каждом из них, исходя из гексагональной конфигурации созвездия, можно получить соответствующий ряд значений: 4 r ²; 32 r ²/3; 123 r ²/6; 284 r ²/10; и т. д.

Результаты расчётов зависимостей C(Q) и N₀(Q) для гексагонального созвездия N-QAM показаны на рис. 31 и 32 кривыми 3. Для сопоставления полученных оценок на рис. 31 приведена также зависимость – формула К. Шеннона (кривая Ш ) а также C_ц(Q) = 2 C(Q) – кривая ШК.

N₀

120

100

80

60 3

40 2

20 1

0

1 3 10 30 100 300 Q

Рис. 32. Сравнительная оценка оптимального количества сигнальных позиций

современных цифровых каналов радиосвязи

Таким образом, сравнительные оценки пропускной способности современных цифровых каналов радиосвязи, проведённые предложенным в разд. 12 упрощенным методом, позволяют сделать следующие выводы (см. рис. 31 и 32).

1. Современные цифровые каналы радиосвязи обладают значительно большей пропускной способностью, чем аналоговые, для которых формула Шеннона даёт верхнюю границу при больших значениях отношения сигнал/помеха Q. Например, при значениях Q > 10 модуляция N-PSK даёт относительно формулы Шеннона на 1,15 (бит/с) большее значение величины C(Q).

Более точные оценки (см. ниже) дают выигрыш около 0,8 (бит/с).

2. При значениях отношения сигнал/помеха Q, меньших 10, следует применять фазовую манипуляцию N-PSK: от двухпозиционной до восьмипозици-

онной. При величине Q ≥ 20 целесообразно перейти к 16-позиционной квадратурной амплитудной модуляции с квадратным созвездием. На гексагональное созвездие, которое довольно сложно в реализации, лучше всего переходить при Q ≥ 50. В последнем случае пропускная способность аналоговых каналов радиосвязи при Q = 100 ограничена величиной 3,3, а цифровых каналов – величиной 6,5 (бит/с).

3. Проведённые сравнительные характеристики пропускной способности C_ц(Q) и оптимального количества позиций N₀(Q) цифровых систем электросвязи требуют уточнения, поскольку для реальных линий электросвязи характерны помехи, распределение которых в первом приближении следует аппроксимировать гауссовским законом.