10. Помехоустойчивое канальное кодирование Основные понятия и классификация избыточных кодов

Выше мы определили коэффициент информационной надёжности χ(П) канала передачи дискретных сообщений, имеющего переходную матрицу П, как отношение максимальной – по всем возможным источникам ДИС – удельной информативности системы «ДИС–КПДС» к удельной информативности (энтропии) источника ДИС, согласованного с каналом КПДС. Каким образом можно практически реализовать максимально возможную (теоретическую) информационную надёжность системы передачи семиотической (знаковой, дискретной) информации?

Во-первых, для такой оптимальной (по критерию максимальной информационной надёжности канала КПДС) системы «ДИС–КПДС» следует – согласно байесовскому критерию (максимума апостериорной вероятности) – определить правила присвоения выходным символам w_k (k = 1, 2, …, N ) значений входных знаков (первичных символов) u_j ( j = 1, 2, …, N ).

Во-вторых, при произвольном источнике ДИС с помощью кодовых символов v_r (r = 1, 2, …, M ) снять избыточность данного источника ДИС.

В-третьих, перекодировать поток символов S_i⁽ⁿ⁾ = ( v_i1, v_i2, …, v_il, …) таким образом, чтобы соответствующие кодовые блоки имели априорные вероятности, соответствующие источнику ДИС, согласованному с данным каналом КПДС.

Если эти условия выполнены, то при произвольном источнике ДИС, имеющем удельную информативность (энтропию)

(бит/знак),

любое достаточно длинное (n >> 1) сообщение (последовательность, или текст) S_i⁽ⁿ⁾ = ( u_i1, u_i2, …, u_il, …, u_in ), несущее в себе количество информации

I(S_i⁽ⁿ⁾) ≈ n ≡ n H(U),

будет передаваться по каналу КПДС, в котором имеются помехи и который обладает переходной матрицей П, в искажённом виде.

В результате действия в канале КПДС помех при передаче сообщения S_i⁽ⁿ⁾ длины n >> 1 на выходе канала мы получим максимально возможное, при данных ДИС и КПДС, количество информации: I_вых(S_i⁽ⁿ⁾) ≈ n χ(П) H(U), или I_вых(S_i⁽ⁿ⁾) ≤ n H(U). То есть если бы в канале КПДС помехи отсутствовали, то данное количество информации I_вых(S_i⁽ⁿ⁾) мы могли бы передать с помощью m = n χ(П) знаков; при этом m ≤ n.

Потеря информации в канале КПДС происходит из-за того, что выбранное нами оптимальное правило присвоения выходным символам {w_k}значений входных знаков {u_j}приводит к некоторомуминимальному количеству ошибок, которые мы не обнаруживаем. Если бы мы обнаруживали эти ошибки (и не воспринимали ошибочные символы), а ещё лучше – их исправляли, то с помощью последовательности S_i⁽ⁿ⁾ = ( u_i1, u_i2, …, u_il, …, u_in ) из n входных знаков, где первые m = n χ(П) знаков – информационные, а k = n – m = n [1 – χ(П)] – проверочные, мы могли бы передавать по каналу КПДС с помехами почти безошибочно количество полезной информации I(S_i⁽ⁿ⁾) ≈ m ≡ m H(U) (бит).

При этом: чем надёжнее канал КПДС, тем меньший процент проверочных знаков нужно включать в передаваемую последовательность S_i⁽ⁿ⁾ и тем меньше будет вероятность ошибочной идентификации знаков u_j. Поскольку проверочные символы также подвержены в канале КПДС искажениям, то при χ(П) = 0 никакими «ухищрениями» мы не сможем исправить ту ситуацию, при которой апостериорная вероятность P(w_k |u_j) не связана с априорной P(u_j), ибо соответствующие проверочные символы, подаваемые на вход канала КПДС, никак не повлияют на его выход. В симметричном бинарном канале КПДС в этом случае и информационные знаки, и проверочные символы будут идентифицироваться на выходе КПДС с вероятностью 1/2, то есть канал КПДС, согласно К. Шеннону, можно «смело заменить бросанием монеты».

Для того чтобы реализовать представленные формально-математические результаты, следует искусственно ввести избыточность при передаче сообщений {u_j}с помощьюпроверочных символов, которые по определённому алгоритму, известному получателю ПИ (или зашитому в память декодера), «привязываются» к передаваемым (информационным) знакам {u_j}или, лучше, к информационным блокам. Это называется помехоустойчивым, или канальным, или избыточным кодированием и аналогично передаче телефонных сообщений «по буквам»: «а» – Антон, «б» – Борис и т. п.

Современные информационные системы в качестве переносчиков информации используют кодовые слова, состоящие из независимых (после соответствующего кодирования знаков {u_j}источникаДИС) символов “единица” и “ноль”: V = {v₁, v₂} = {1, 0} – бинарные каналы КПДС. Кодер источника снимает избыточность источника ДИС. Если канал КПДС – симметричный, то дополнительного согласования источника ДИС и канала КПДС в этом случае не потребуется.

При передаче символов “1” и “0” по каналу КПДС с помехами можно, например, утраивать их: “1” передавать как “111”, а “0” – как “000”. Тогда при воздействии на канал КПДС относительно слабых помех на выходе канала может появиться, например, тройка “101” или “100” и т. п. Если полученной на выходе канала КПДС тройке “101” приписывать передачу по каналу КПДС “единицы”, а “100” – “ноля” и т. п. (мажоритарное декодирование), то потери информации в канале КПДС минимальны – и канал становится почти абсолютно надёжным.

Однако такой способ помехоустойчивого кодирования «слишком дорогой». Поэтому обычно бинарный поток “единиц” и “нолей” разбивают на достаточно длинные блоки, которые снабжают несколькими «проверочными битами» (канальное кодирование), а на приёмной стороне канала КПДС путём анализа блоков обнаруживают и исправляют (или нет) ошибки в полученном блоке.

Простейшее блочное кодирование – передача информации по байтам. Байт содержит восемь (или 16, или 32) информационных «битов» (символов “0” и “1”), один проверочный «бит», один – стартовый и два – стоповых (границы байта). Проверочный «бит» добавляется по правилу: если в информационных «битах» содержится чётное количество «единиц», то к этим «битам» добавляется “ноль”, если нечётное – то “единица”. На приёмной стороне КПДС полученный байт проверяется на чётность: если количество “единиц” – нечётное, то байт забраковывается, поскольку определить и исправить в этом случае искажённый «бит» невозможно. Если мы проводим работу на ПК, то в этом случае компьютер «зависает», и обнаруженный в ПК неправильный байт не приводит к дальнейшим вредным для функционирования ПК последствиям.

Если в передаваемом байте присутствуют две ошибки, то байт не будет забракован – и будет разрушать информацию при всех дальнейших операциях на ПК. Чтобы этого не произошло, применяют операцию перемежения. Для этого берут, например, два последовательных блока по восемь «битов» и размещают информационные «биты» в следующей последовательности: v₁, v₉, v₂, v₁₀, v₃, v₁₁, …, v₈, v₁₆. «Биты чётности» a₁ и a₂ этих блоков размещают после восьмого (a₁) и после шестнадцатого (a₂) информационных «битов».

Затем из первых девяти символов формируют первый байт, из вторых – второй. На выходе канала КПДС в полученных двух байтах восстанавливают последовательность первоначальных блоков: v₁, v₂, v₃, …, v₈, a₁; v₉, v₁₀, v₁₁, …, v₁₆, a₂. Если в каком-либо из посланных байтов на выходе канала КПДС допущены две ошибки, идущие подряд, то в результате восстановления первоначальных байтов они будут разнесены по одной на каждый байт – и обнаружены. Таким образом, перемежение является методом борьбы с «групповыми» (идущими подряд) ошибками в канале КПДС.

Существует множество других способов помехоустойчивого канального кодирования (см. Прил. 3), методы разработки которых составляют содержание отдельной дисциплины прикладной математики: теория избыточного, или помехоустойчивого кодирования (подробнее см., например [13, 14, 33, 34, 45]).

Однако математическая теория информации К. Шеннона позволяет сформулировать предельные соотношения между удельной информативностью (энтропией) источникаДИС и удельной информационной ёмкостью ℰ(Π) ≡ _макс(П) статического канала КПДС вне зависимости от способа помехоустойчивого канального кодирования (см. заключении по разд. 9).

Сущность помехоустойчивого кодирования (избыточности кодов) заключается во введении в закодированное сообщение S_i⁽ⁿ⁾ = w_i1, w_i2, …, w_{i n}, почти не имеющее избыточности после прохождения сообщением кодера источника, некоторой «управляемой» избыточности. Задача помехоустойчивого кодирования заключается в добавлении к информационным символам первичных кодовых слов дополнительных символов таким образом, чтобы декодер сообщений мог бы найти и даже исправить ошибки, возникающие из-за воздействия помех при передаче закодированных сообщений по линиям электросвязи.

Существует множество различных способов введения управляемой избыточности в помехоустойчивые (избыточные) коды.

Избыточные коды делятся на блочные и непрерывные.

В блочных кодах передаваемая информация разбивается на отдельные блоки – кодовые комбинации, которые кодируются и декодируются независимо. Если число символов (элементов) первичного кода (длина информационного блока) равно m, а вводимых дополнительных проверочных символов (элементов) кода равно k, то общее число символов (элементов) в кодовой комбинации блочного избыточного кода равно n = m + k.

В непрерывных кодах передаваемая информационная последовательность символов не разделяется на блоки, а проверочные символы размещаются в определенном порядке между информационными. Среди непрерывных кодов особое место занимают свёрточные коды.

Блочные коды бывают равномерными (кодовые слова имеют одинаковые длины) и неравномерными. Равномерные коды делятся на разделимые и неразделимые. В разделимых кодах информационные и проверочные символы во всех кодовых комбинациях занимают одни и те же позиции. Поэтому разделимые коды обозначаются как (n, m)-коды.

В неразделимых кодах деление на информационные и проверочные символы отсутствует.

Разделимые коды делятся на линейные и нелинейные. Первые названы так потому, что их проверочные символы представляют собой линейные комбинации информационных символов. Важное место среди линейных кодов образуют циклические коды.

Нелинейные коды характеризуются наличием двух и более проверок внутри каждой кодовой комбинации.

Интегральной (обобщённой) характеристикой всех помехоустойчивых кодов, как и для случая реальных источников ДИС с избыточностью, является коэффициент избыточности кода k. Например, поскольку с помощью блочных разделимых (n, m)-кодов, которые имеют длину информационных блоков m, а общую длину блоков n, в отсутствие помех можно передавать I_n = log 2ⁿ = n (бит/знак) информации, а передаётся только I_m = log 2^m = m (бит/знак), то коэффициент избыточности такого кода следует определить как

k_пк = (I_n – I_n)/I_n = (1 – m/n).

Значение этого коэффициента лежит в пределах от k_пк = 0 (при k = n – m = 0) до k_пк→ 1 при k → ∞.

Значит, можно утверждать:

для того чтобы обеспечить надёжную передачу дискретной (знаковой) информации с помощью заданной статической системы ССПИ при наличии в её линии электросвязи (КПДС) помех, необходимо, чтобы применяемый для этого помехоустойчивый код имел избыточность, не меньшую, чем информационная ненадёжность канала КПДС. Иначе в канале КПДС будет происходить не менее 100 [1 – χ(Π) – kпк] процентов потерь информации при любом способе кодирования сообщений с помощью кода с данной величиной kпк.

Каким образом можно формализовать процедуры избыточного кодирования и декодирования бинарного информационного потока со снятой избыточностью: S_i⁽ⁿ⁾ = (v_i1, v_i2, …, v_{i l}, …, v_{i n})?

Рассмотрим бинарное разделимое блочное кодирование.

В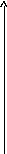простейшем случае это (3, 2)-коды. То есть информационных кодовых комбинаций (блоков) всего четыре:w₁ = (0, 0), w₂ = (1, 0), w₃ = (0, 1) w₄ = (1, 1).

Для наглядности их можно представить на плоскости (x, y) в системе координат (x, y, z) – см. рис. 10.

z =(011)

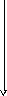
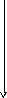
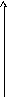
=(101)

y

w₃ w₄

w₁ w₂

x

Рис. 10. Простейший блочный код (3, 2)

Ясно, что любая (одна) ошибка декодирования приводит к «перепутыванию» блоков {w_j}и к необнаруживаемой ошибке приёма знаковой информации. Однако если мы «грамотно» добавили проверочные символы, то одну ошибку в блоке при декодировании кодовых блоков можно обнаружить и попросить источник ИС, например, повторить передачу именно этого блока.

Для этого мы можем поступить следующим образом (см. рис. 10).

Если передаётся информационный блок w₁, то его избыточный кодовый блок будет ; еслиw₂, то ; еслиw₃, то и, наконец, еслиw₄, то .

Ясно, по построению, что любую одиночную ошибку мы обнаружим.

Переведём эти эвристические соображения на язык линейной алгебры. Для этого запишем информационные кодовые блоки множества символов {w_j}в виде вектор-столбцов:

, ,,.

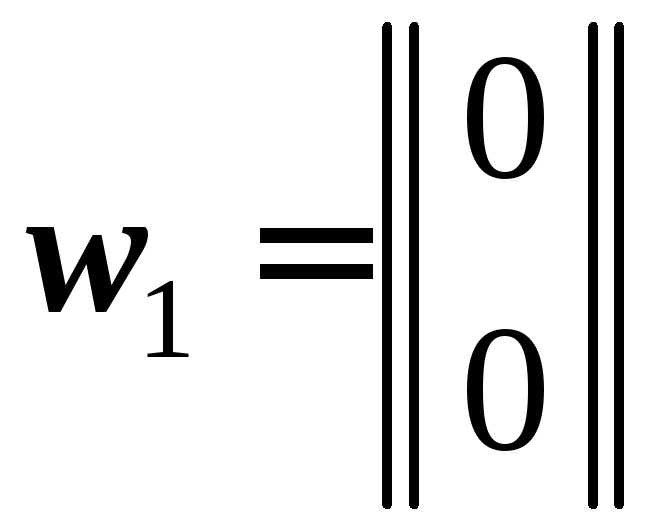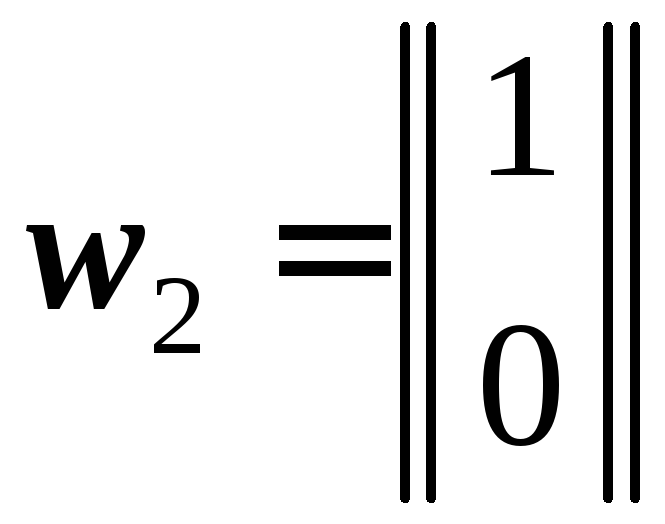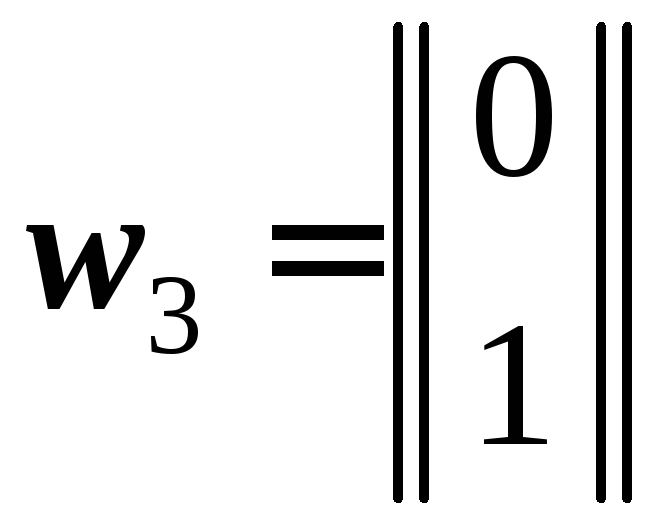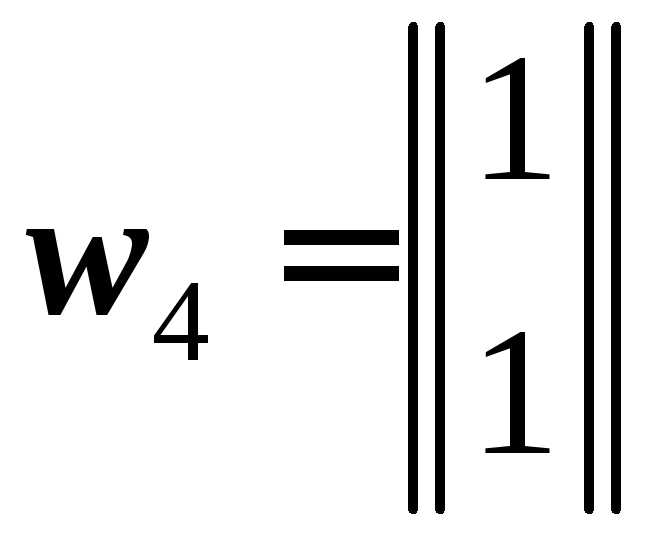Тогда процесс кодирования можно представить линейным преобразованием A вектор-столбцов размера 2 ×1 в вектор-столбцы размера 3 ×1, то есть матрица этого преобразования A будет иметь размер 3 × 2: , где– кодовый блок избыточного кода для блокаw_j; j = 1, 2, 3, 4

Можно проверить, что в данном случае матрица кодирования имеет вид:

,

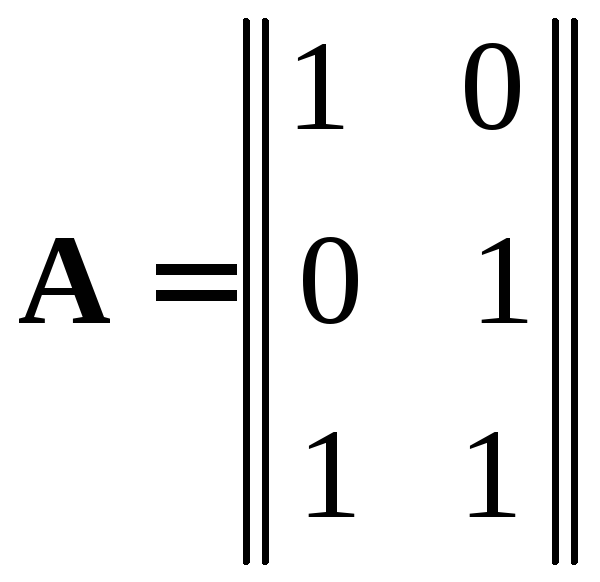если ввести суммирование по модулю два, обозначив эту операцию как .

Действительно. Поскольку верхняя часть матрицы A является единичной квадратной матрицей порядка 2 (то есть размера 2×2), то в кодовые блоки войдут кодовые блокиw_j, а проверочные элементы (символы) a_j суть: .

Для декодирования мы должны построить такую матрицу B размера 2 ×3, чтобы получить тождество: , или, гдеE – единичная матрица порядка 2 (размера 2 ×2).

Отсюда получаем уравнение для нахождения матрицы B: B A = E. Это не значит, что B = A^–1, поскольку для прямоугольных матриц A обратные матрицы A^–1 не определены.

Таким образом, для нахождения матрицы B операции декодирования B нужно по матрице A найти такую псевдообратную матрицу, чтобы выполнялось тождество: B A = E, в котором размеры матриц B, A и E – 2 ×3, 3 ×2 и 2 ×2 соответственно.

Из уравнения B A = E вытекает система только четырёх уравнений:

.

«Чистые математики» разработали методы решения такого рода недоопределённых систем уравнений и нахождения псевдообратных матриц B. В данном случае матрица B имеет вид:

.

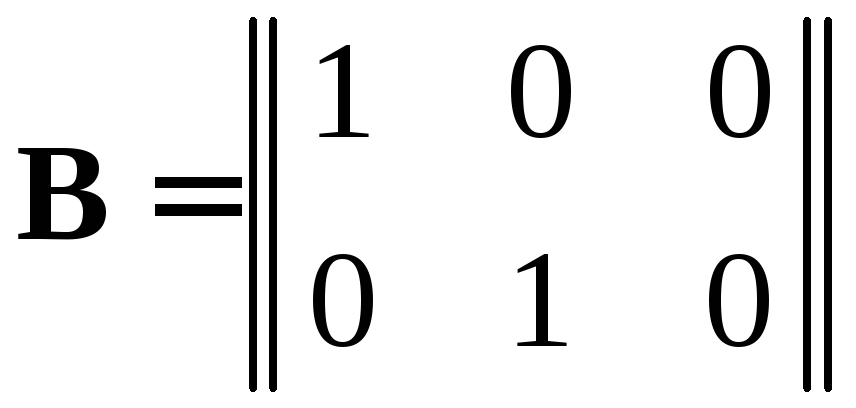Путём непосредственной проверки можно убедиться, что B A = E:

×=.

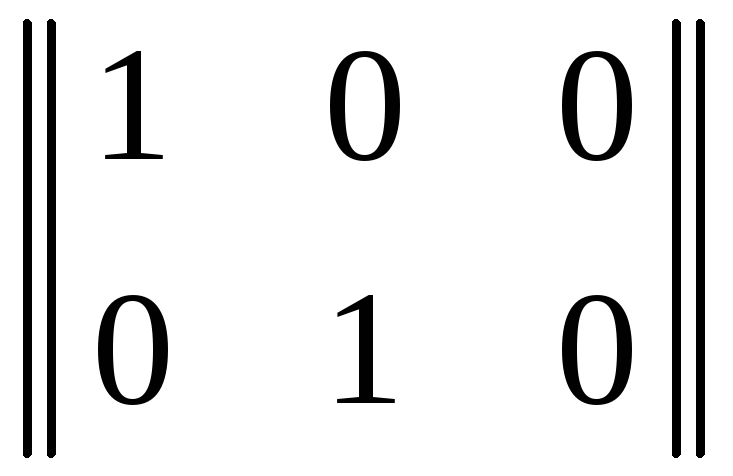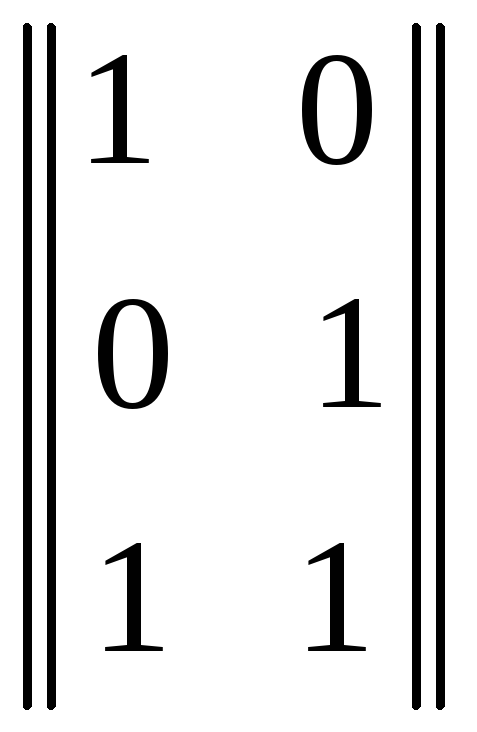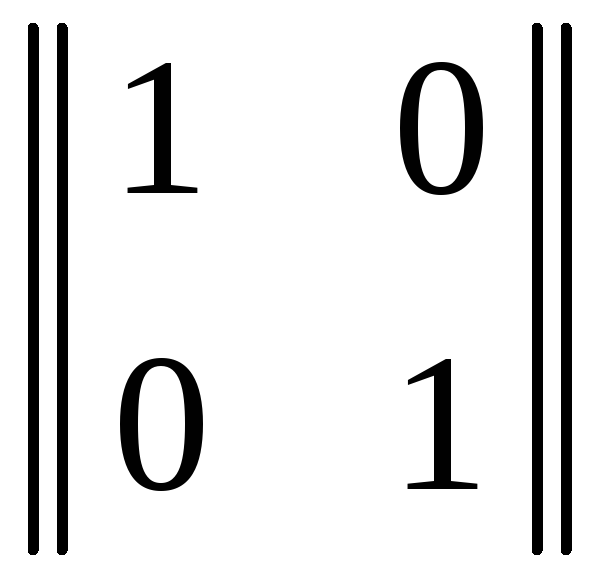Однако прежде, чем переходить к декодированию принимаемого блока

, необходимо проверить, нет ли в этом блоке ошибки? Для этого можно, например, перемножить принимаемый вектор с вектором-строкойh = || 1 1 1 ||: h ⊗=a_j. Если выполняется равенство h ⊗=a_j = 0, то в принятом блоке нет ни одной однократной ошибки; если h ⊗=a_j = 1 – имеется ошибка, исправить которую не представляется возможным.

Действительно:

h ⊗ = || 1 1 1 ||· = 0; h ⊗ = || 1 1 1 || ⊗ = 11 = 0;

h ⊗ = || 1 1 1 || ⊗ = 11 = 0;h ⊗ = || 1 1 1 ||⊗ = 11 = 0;

|| 1 1 1 ||⊗ = 1; || 1 1 1 ||⊗ = 1; || 1 1 1 ||⊗ = 1; || 1 1 1 ||⊗ = 111 = 1.

Для обобщения рассмотренного выше примера введём