
- •Математическая логика
- •Раздел I. Алгебра высказываний
- •1. Высказывания и операции над ними. Формулы
- •2. Следование, эквивалентность и преобразование формул
- •3. Использование законов логики в доказательстве теорем и построении схем
- •Преобразуем эту формулу, используя соответствующие эквивалентности u
- •4. Булевы функции
- •5. Нормальные формы
- •5. Полные системы операций. Алгебра Жегалкина
- •6. Выводимость
- •Раздел II. Алгебра предикатов
- •1. Предикат. Операции над предикатами.
- •2. Модель. Формула алгебры предикатов сигнатуры .
- •3. Формулы алгебры предикатов
- •Основные общезначимости алгебры предикатов
- •Раздел 3. Логические исчисления
- •1. Определение формального исчисления
- •2. Исчисление высказываний ив.
- •3. Отношение эквивалентности в ив
- •4. Исчисление секвенций ис.
- •Исчисления предикатов ип (ипс).
- •Прикладные исчисления предикатов.
- •Автоматическое доказательство теорем
- •Теория алгоритмов
- •Машины Тьюринга
- •2. Рекурсивные функции
- •3. Временная сложность алгоритма. Классы p и np.
- •4. Полиномиальная сводимость. Np-полные языки и задачи.
6. Выводимость
Пусть задано
множество формул от высказывательных
переменных
![]()
![]() (
(![]() ),
),![]() (
(![]() ),
. . . ,
),
. . . ,![]() (
(![]() ).
(1)
).
(1)
Это множество формул назовем системой посылок.
Определение.
Формула
![]() (
(![]() )
называется выводимой из системы формул
(1) в алгебре высказываний, что обозначается
)
называется выводимой из системы формул
(1) в алгебре высказываний, что обозначается![]() ,
. . ,
,
. . ,![]()
![]()
![]() ,
тогда и только тогда, когда формула
,
тогда и только тогда, когда формула
![]() (2)
(2)
является
ТИ-высказыванием, т.е.
![]() .
.
Из определения следует, что если конъюнкция
![]() (3)
(3)
тождественно истинна, то из такой системы посылок (1) выводимы только тождественно истинные формулы, которые выводимы из любой системы посылок. Если же конъюнкция (3) тождественно ложна, то из системы посылок (1) выводима любая формула.
Если формула
![]() выводима из системы формул (1), то из
истинности всех формул системы при
некоторых значениях высказывательных
переменных
выводима из системы формул (1), то из
истинности всех формул системы при
некоторых значениях высказывательных
переменных![]() следует истинность формулы
следует истинность формулы![]() при тех же значениях переменных.
при тех же значениях переменных.
Нетрудно доказать следующие свойства выводимости.
Если

 и
и
 то
то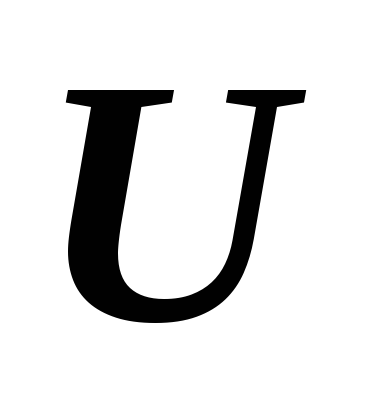
 .
.Если

 и
и ~
~ ,
то
,
то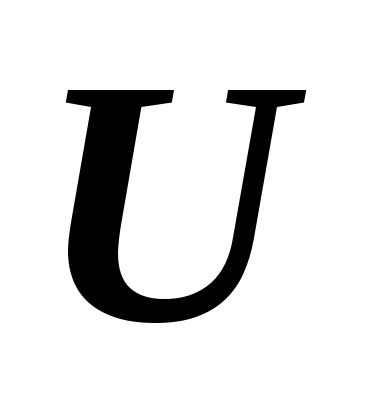
 .
.
Проверка выводимости
формулы
![]() из системы посылок (1) непосредственно
по определению, т.е. путем доказательства
тождественной истинности формулы (2),
достаточно громоздко. Рассмотрим более
простой способ доказательства выводимости
формулы
из системы посылок (1) непосредственно
по определению, т.е. путем доказательства
тождественной истинности формулы (2),
достаточно громоздко. Рассмотрим более
простой способ доказательства выводимости
формулы![]() из системы посылок (1), для которых
конъюнкция (3) не является ни ТИ-высказыванием,
ни ТЛ-высказыванием.
из системы посылок (1), для которых
конъюнкция (3) не является ни ТИ-высказыванием,
ни ТЛ-высказыванием.
Теорема 7.1.
Формула
![]() (
(![]() )
тогда и только тогда выводима из системы
формул (1), когда все полные элементарные
дизъюнкции формулы
)
тогда и только тогда выводима из системы
формул (1), когда все полные элементарные
дизъюнкции формулы![]() входят в СКН-форму
входят в СКН-форму![]() ,
эквивалентную формуле (3) относительно
высказывательных переменных
,
эквивалентную формуле (3) относительно
высказывательных переменных![]() .
.
Так как теорема 1 формулирует необходимое и достаточное условие выводимости формулы, то на основе нее можно сформулировать алгоритм доказательства выводимости формулы.
Из системы посылок (1) строится конъюнкция (3).
Находим СКН-форму от высказывательных переменных для формулы (3).
Строим СКН-форму для формулы
 и проверяем вхождение полных элементарных
дизъюнкций СКН-формы для формулы
и проверяем вхождение полных элементарных
дизъюнкций СКН-формы для формулы в СКН-форму для формулы (3).
в СКН-форму для формулы (3).
Задание 1.
Доказать выводимость
![]()
![]() .
.
Решение.
Обозначим
 =X,
=X,
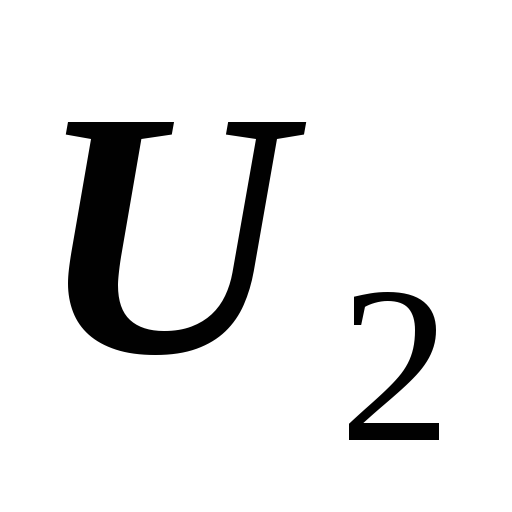 =
= .
Строим их конъюнкцию
.
Строим их конъюнкцию .
.Найдем СКН-форму
 эквивалентную этой конъюнкции.
эквивалентную этой конъюнкции.
![]() V
V
Получим СКН-форму для формулы B
 .
.
![]()
Так как обе
дизъюнкции входят в СКН-форму
![]() ,
то выводимость доказана.
,
то выводимость доказана.
Замечание.
Выводимость формулы
![]() можно получить и без нахождения ее
СКН-формы. Для этого нужно преобразовать
с помощью известных эквивалентностей
формулу (3) или даже конъюнкцию некоторых
полных дизъюнкций из этой СКН-формы.
Например, конъюнкция 1-ой и 3-ей полных
дизъюнкций формулы
можно получить и без нахождения ее
СКН-формы. Для этого нужно преобразовать
с помощью известных эквивалентностей
формулу (3) или даже конъюнкцию некоторых
полных дизъюнкций из этой СКН-формы.
Например, конъюнкция 1-ой и 3-ей полных
дизъюнкций формулы![]() из задания 1 преобразуется с помощью
формулы склеивания к искомой формуле.
из задания 1 преобразуется с помощью
формулы склеивания к искомой формуле.
![]()
Кроме того, воспользовавшись теоремой 1, можно построить все СКН-формы выводимые из данной системы посылок. Для этого требуется небольшая модификация алгоритма доказательства выводимости формулы. После построения СКН-формы для формулы (3) необходимо
3. Из полных элементарных дизъюнкций полученной СКН-формы строим различные комбинации конъюнкций. Эти конъюнкции и будут исчерпывать все СКН-формы, выводимые из системы посылок (1).
Раздел II. Алгебра предикатов
Алгебра предикатов является развитием алгебры высказываний. Кроме простых и составных высказываний она вводит в рассмотрение высказывания, отнесенные к переменным из некоторого множества M, которое в дальнейшем будем называть предметным множеством, а его элементы – предметными переменными.
