ЛЕКЦИИ ТЕОРМЕХ / Лек6Д(през)

Тема: ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

Лекция 6Д

Работа силы. Теорема об изменении кинетической энергии материальной точки, механической энергии и твердого тела

1. Работа постоянной и переменной силы.

2. Работа силы тяжести и силы упругости.

3. Мощность.

4. Работа и мощность сил, приложенных к твердому вращающемуся телу.

1. Работа постоянной и переменной силы.

(6.1) (6.2)

Случай переменной по модулю и направлению силы

Естественный способ задания движения точки

(6.3) (6.4)

Векторный способ задания движения точки

(6.5)

Координатный способ задания движения точки

(6.6)

Работа силы `Р на конечном перемещении равна сумме её работ на элементарных участках

Пользуясь выражениями элементарной работы и переходя к пределу при стремлении числа участков к бесконечности, получаем следующие выражения работы силы на конечном перемещении М₁ М₂.

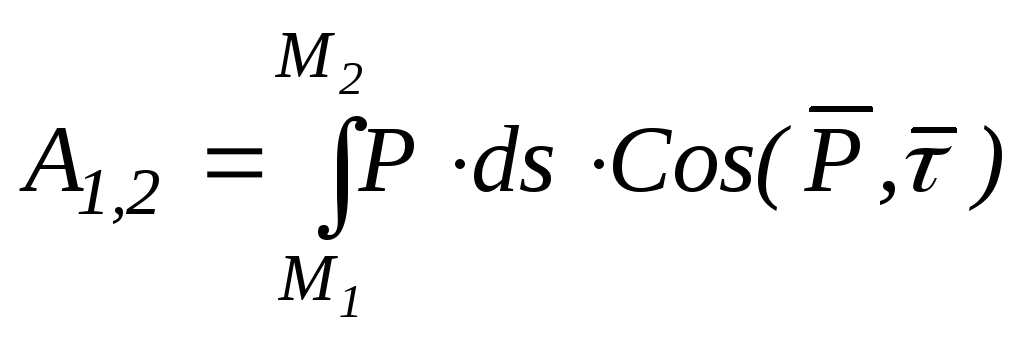(6.7)

(6.8)

(6.9)

(6.10)

Следовательно, работа силы на любом перемещении М₁М₂ равна взятому вдоль этого перемещения интегралу от элементарной работы.

Пример: работа силы при растяжении образца

2. Определение работы силы тяжести и силы упругости

Работа силы тяжести

	т.к. Х=0, Y=0, Z=-G, то dА = -GdZ (6.11)
Работа силы тяжести равна взятому со знаком «+» или «–« произведению силы тяжести на вертикальное перемещение точки её приложения. Работа силы тяжести не зависит от вида траектории, по которой перемещается точка её приложения, а зависит лишь от расстояния между горизонтальными плоскостями, проходящими через начальное и конечное положение точки.

Работа силы упругости

(6.12)

3. Мощность

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени.

Если в течение малого промежутка времени dt сила `Р совершает работу , то мощность этой силы

(6.13)

Таким образом, мощность силы равна скалярному произведению векторов силы и скорости ее точки приложения.

Аналитическое выражение мощности силы имеет вид

(6.14)

Из (6.13) следует

если направления и совпадают, то

4. Работа и мощность сил, приложенных к твердому вращающемуся телу.

(6.15) Если при вращении тела значение его угла поворота изменяется от j1 до j2, то сумма работ сил на этом конечном перемещении (6.16) В случае, если главный момент внешних сил относительно оси вращения тела постоянен, (6.17) То есть сумма работ сил на конечном перемещении тела равна произведению главного момента внешних сил относительно оси вращения на конечное изменение угла поворота тела.