ЛЕКЦИИ ТЕОРМЕХ / Лекция8ППоле
.docТема: ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Лекция 8Д
Потенциальное силовое поле
-
Потенциальное силовое поле и силовая функция.
-
Потенциальная энергия.
-
Примеры потенциальных силовых полей.
-
Закон сохранения механической энергии.
-
Потенциальное силовое поле и силовая функция.
Силовым полем называют часть пространства, в каждой точке которого на материальную точку действует определённая сила, зависящая от координат точки.
Силовое поле считают стационарным, если действующие силы не изменяются с изменением времени. Если же силы зависят от времени, то силовое поле является нестационарным.
|
|
Стационарное силовое поле называют потенциальным, если существует такая функция U, зависящая от координат точки, через которую проекции силы F на координатные оси в каждой точке поля выражаются так:
Г `F на координатной оси. Функцию U(x,y,z) называют силовой функцией.
|
|
Основные свойства силовой функции |
|
|
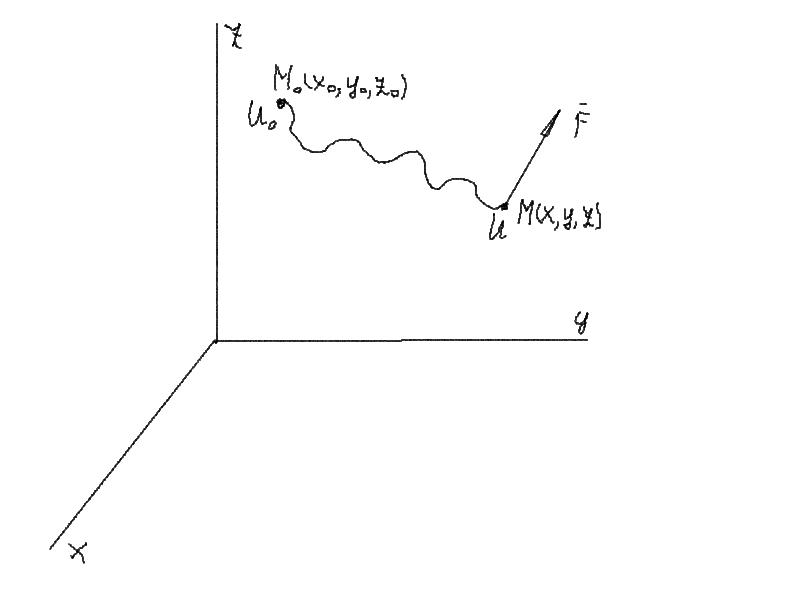
1) Элементарная работа силы в потенциальном силовом поле равна полному дифференциалу от силовой функции.
|
|
|
2) Полная работа силы на каком-либо перемещении точки равна разности значений силовой функции в конечной и начальной точках перемещения и не зависит от формы траектории, по которой оно совершается.
|
|
|
3) Если применить понятие вектора-градиента от силовой функции U то силу `F можно выразить как градиент силовой функции U |
|
|
Определим условия, которые позволяют по силам силового поля устанавливать, будет ли силовое поле потенциальным. |
|
|
Если силовая функция U существует, то
так как
то
Аналогично можно получить |
|
|
Или
rot`F = 0 |
|
|
Таким образом, для того, чтобы силовое поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым.
|
|
2. Потенциальная энергия
Потенциальной энергией П силового поля в точке М называется работа, которую совершают силы поля при перемещении материальной точки М в начальную точку Мо.
|
|
|
|
То есть потенциальную энергию в какой-либо точке поля с точностью до несущественной постоянной можно определить как значение силовой функции в этой же точке, взятое со знаком минус.
|
|
|
Потенциальная энергия точки
|
|
|
Геометрическое место точек в пространстве, в которых потенциальная энергия материальной точки имеет одно и то же значение, определяется из уравнения
Это уравнение определяет некоторую поверхность в пространстве, которая называется поверхностью равного потенциала или эквипотенциальной поверхностью. |
|
3. Примеры потенциальных силовых полей
Поле силы тяжести
|
|
Тогда уравнение эквипотенциальной поверхности имеет вид
|
|
Для механической системы
То есть потенциальная энергия механической системы, находится под действием силы тяжести, равна произведению веса системы на высоту её центра тяжести над нулевой эквипотенциальной поверхностью. |
|
Поле линейной силы упругости
|
|
Так как
|
|
Следовательно,
поверхностями уровня
|
|
4. Закон сохранения механической энергии
Для материальной точки
Теорема об изменении кинетической энергии запишется:
![]()
Если материальная точка движется в потенциальном силовом поле, то
![]()
Следовательно
![]()
или
![]()
где h – постоянная величина
Обозначая Е – полную механическую энергию точки
![]()
При движении точки в потенциальном силовом поле её полная механическая энергия остаётся постоянной величиной.
Для механической системы
Теорему об изменении кинетической энергии для системы можно записать
![]()
Если система движется в потенциальном силовом поле, то
![]()
где П – потенциальная энергия внутренних и внешних сил, действующих на систему. Следовательно,
![]()
![]()
Полная механическая энергия при движении системы в потенциальном силовом поле внешних и внутренних сил является постоянной величиной.

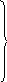

 де
X,
Y,
Z
– проекции силы
де
X,
Y,
Z
– проекции силы