ЛЕКЦИИ ТЕОРМЕХ / Лек5Д(през)

Относительно центра

Момент количества движения mV точки М относительно точки 0 представляет собой вектор L₀, направленный перпендикулярно к плоскости, проходящей через вектор и центр О в ту сторону, откуда вектор относительно центра О виден направленным против вращения часовой стрелки.

(5.1)

(5.2)

Относительно оси

Момент L_z количества движения т. М относительно оси Z равен (взятому со знаком + или -) произведению проекции вектора на плоскость I, перпендикулярную к оси Z, на плечо этой проекции относительно т. О пересечения оси Z с плоскостью I.

(5.3)

(5.4)

Связь между моментами силы относительно центра и оси, проходящей через этот центр

То есть проекция момента количества движения материальной точки относительно некоторого центра на ось, проходящую через этот центр, равна моменту количества движения точки относительно этой оси.

Аналитические выражения моментов количества движения точки относительно осей координат

(5.5)

Относительно центра

Кинетическим моментом или главным моментом количеств движения механической системы относительно данного центра называется вектор, равный геометрической сумме моментов количеств движения всех материальных точек системы относительно этого центра.

(5.6)

Относительно оси

Кинетическим моментом, или главным моментом количеств движения механической системы относительно оси, называется алгебраическая сумма моментов количеств движения всех материальных точек системы относительно этой оси.

(5.7)

Кинетический момент системы относительно центра

Кинетический момент системы относительно оси

Относительно центра

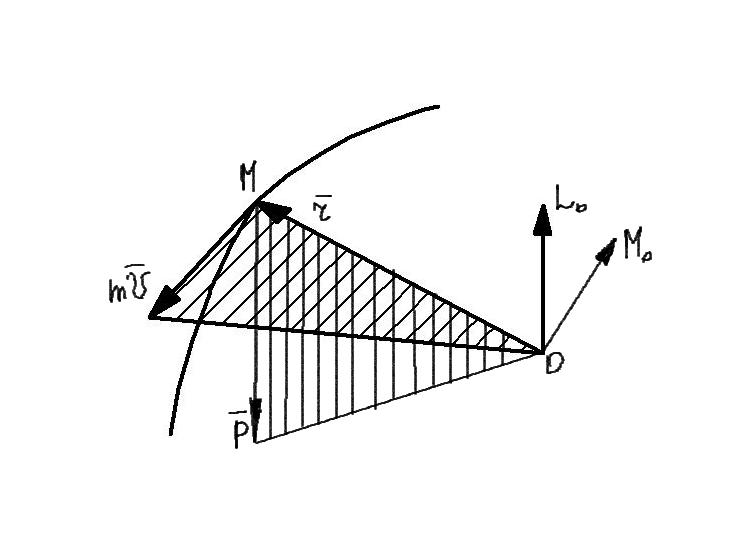
Определим момент силы Р относительно центра О

Определим также момент количества движения т.М относительно центра О

Установим зависимость между моментом количества движения т.L_o и моментом силы М_о

;

(5.8)

Если на материальную точку действует несколько сил

(5.9)

Производная по времени от момента количества движения материальной точки относительно некоторого неподвижного центра равна геометрической сумме моментов сил, действующих на точку, относительно того же центра.

Относительно оси

В проекциях на оси координат уравнение (2.9) запишется:

(5.10)

Здесь L_x, L_y, L_z – моменты количества движения т.М относительно осей координат, а М_ix, M_iy, M_iz – моменты силы P_i относительно этих же осей.

Производная по времени от момента количества движения материальной точки относительно некоторой неподвижной оси равна алгебраической сумме моментов сил, действующих на точку, относительно этой же оси.

Следствия из теоремы

1. Если линия действия равнодействующей приложенной к материальной точке сил всё время проходит через некоторый неподвижный центр, то момент количества движения материальной точки относительно этого центра остаётся постоянным.

Если то , и

2. Если момент равнодействующей приложенных к материальной точке сил относительно некоторой оси всё время равняется нулю, то момент количества движения материальной точки относительно этой оси остаётся постоянным.

Если то , и

Относительно центра

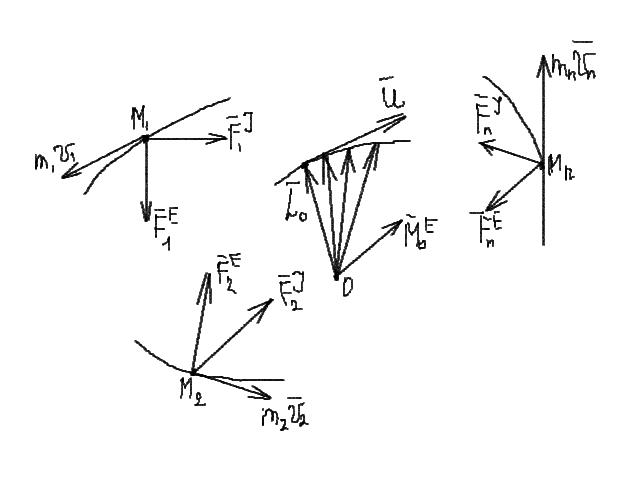
Положим, что система материальных точек М₁, М₂,…,М_n движется под действием некоторой системы сил, которые разделим на внешние силы и внутренние силы:

Выберем некоторый неподвижный центр О и определим изменение момента количества движения каждой точки M_i относительно этого центра по уравнению

Просуммируем полученные n уравнений

(а)

Так как геометрическая сумма моментов всех внутренних сил относительно любого центра равна нулю, то есть

преобразуем левую часть равенства (а)

Тогда уравнение (а) принимает вид

(5.11)

Производная по времени от кинетического момента механической системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему относительно того же центра.

Относительно оси

Векторному равенству (2.11) соответствует три равенства в проекциях на оси координат

(5.12)

Здесь L_x, L_y, L_z – кинетические моменты механической системы относительно оси координат, а - главные моменты внешних сил относительно этих осей.

Уравнения (2.12) показывают, что производная по времени от кинетического момента механической системы относительно некоторой оси равна главному моменту внешних сил относительно этой оси.

Пусть L_о - кинетический момент системы точек М₁, М₂,…,М_n относительно центра О. Система движется под действием внешних сил и внутренних сил .

При движении системы точка А – конец вектора L_o описывает в пространстве некоторую линию, называемую годографом кинетического момента механической системы.

Скорость и движения т.А по годографу определяется векторной производной радиуса – вектора L_o этой точки по времени

с другой стороны на основании доказанной теоремы об изменении момента количества движения

Следовательно

То есть скорость конца вектора кинетического момента механической системы относительно некоторого неподвижного центра геометрически равна главному моменту внешних сил, действующих на эту систему, относительно этого же центра.