
ЛЕКЦИИ ТЕОРМЕХ / Лек4Д(през)
.docТЕМА: ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
Лекция 4Д
ТЕОРЕМЫ ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
-
Количество движения материальной точки и механической системы.
-
Импульс силы.
-
Теорема об изменении количества движения материальной точки.
4. Теорема об изменении количества движения механической системы.
5. Применение теоремы об изменении количества движения к динамике сплошных сред (теорема Эйлера).
1. Количество движения материальной точки и механической системы.
|
Количеством движения материальной точки называется вектор, имеющий направление вектора скорости и модуль, равный произведению массы точки m на модуль скорости её движения V.
|
Проекции вектора
количества движения
|
|
Количеством движения механической системы называется вектор, равный геометрической сумме (главному вектору) количеств движения всех материальных точек этой системы.
|
|
|
Проекции вектораК на оси координат:
|
|
2. Импульс силы
|
|
|
|
Импульс
силы.
Если постоянная по модулю и направлению
сила Р
действует в течение промежутка времени
|
|
|
Чтобы найти
импульс
переменной силы
|
|
|
Проекции
элементарного импульса
|
|
|
Аналогично на оси y и z
|
|
|
Просуммировав проекции элементарных импульсов и перейдя к пределу, получим определённые интегралы по переменной t, представляющие собой проекции импульса S на оси координат
Здесь X = f1(t); Y = f2(t); Z = f3(t) – проекции переменной силы P = P(t) на оси координат. |
|
|
Модуль и направление импульса S определяются по его проекциям
|
|
|
Для постоянной по модулю и направлению силы Р, действующей в течение промежутка времени , формулы (1.6) имеют вид
|
Sx = X; Sy = Y; Sz = Z, |
|
Если к т. М
приложено несколько сил
Умножим обе части этого равенства на dt и проинтегрируем в пределах от t1 до t2
Получим, что импульс равнодействующей нескольких сил за некоторый промежуток времени равен геометрической сумме импульсов составляющих сил за этот же промежуток времени. |
|
|
В проекциях на координатные оси:
|
|
3. Теорема об изменении количества движения для материальной точки:
|
Теорема: Производная по времени от количества движения материальной точки геометрически равна равнодействующей сил, приложенных к этой точке.
Теорема импульсов: Изменение количества движения материальной точки за некоторый промежуток времени равно геометрической сумме импульсов сил, приложенных к точке за тот же промежуток времени.
|
|
|
|
|
4. Теорема об изменении количества движения для механической системы
|
Теорема: Производная по времени от количества движения механической системы геометрически равна главному векторы внешних сил, действующих на эту систему. |
|
|
В проекциях на оси координат:
|
|
|
Следствия из теоремы: |
|
|
1. Если главный вектор внешних сил за рассматриваемый промежуток времени равен нулю, то количество движения механической системы постоянно.
|
|
|
2. Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна. |
|
|
Закон сохранения количества движения системы |
|
|
Теорема импульсов для системы: Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, приложенных к системе, за тот же промежуток времени. |
где
|
|
В проекциях оси координат
|
|
-
Применение теоремы об изменении количества движения к динамике сплошных сред (теорема Эйлера).
|
|
|
|
Теорема Эйлера. Сумма главных векторов объёмных и поверхностных сил, а также векторов секундных количеств движения жидкости, протекающей через два сечения трубы, равна нулю, если векторы секундных количеств движения направить внутрь выделенного сечениями объёма.
|
|
|


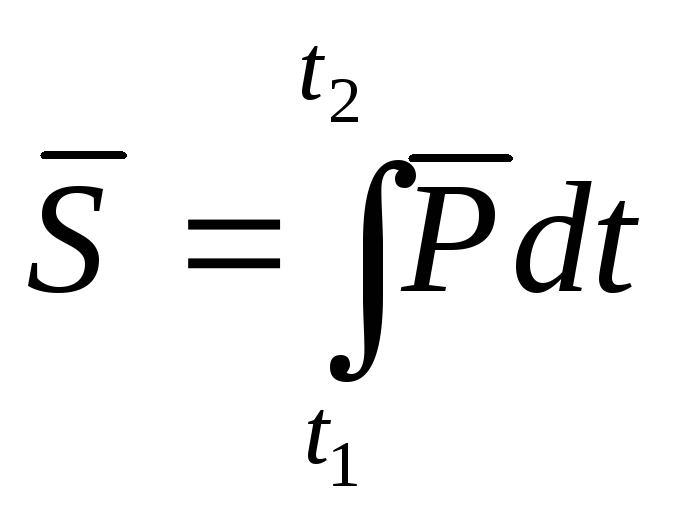 (4.5)
(4.5) ;
;
 ;
(4.6)
;
(4.6)




