ЛЕКЦИИ ТЕОРМЕХ / Лек9Д(през)

ЛЕКЦИЯ 9Д

ДИНАМИКА СФЕРИЧЕСКОГО И СВОБОДНОГО ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА

1. Кинетические моменты твёрдого тела относительно неподвижной точки и координатных осей при его сферическом движении.

2. Дифференциальные уравнения сферического движения твёрдого тела (динамические уравнения Эйлера).

3. Дифференциальные уравнения движения свободного твёрдого тела.

4. Понятие о гироскопе. Гироскоп с тремя степенями свободы.

1. Кинетические моменты твёрдого тела относительно неподвижной точки и координатных осей при его сферическом движении

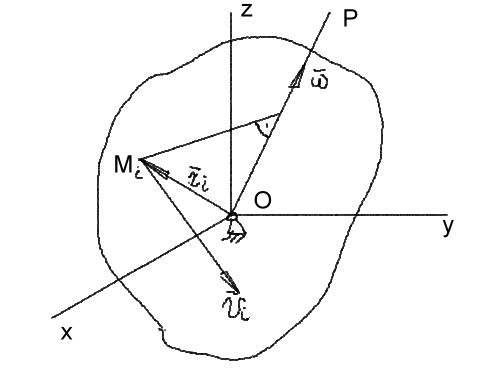
Кинетический момент твёрдого тела, совершающего сферическое движение точки, определяется по общей формуле

(6.1)

так как

(6.2)

где - вектор угловой скорости, направленный по мгновенной оси вращения ОР, - радиус-вектор т. М_i

Рисунок 6.1

Подставим уравнение (6.2) в уравнение (6.1):

(6.3)

Воспользуемся формулой для двойного векторного произведения

так как , а так же

,

то

(6.4)

Определим кинетический момент тела относительно оси х, проходящей через т.О, как проекцию L_о на ось х.

После соответствующих преобразований, получим:

здесь - момент инерции тела относительно оси х,

- центробежный момент инерции тела относительно осей х и у;

- центробежный момент инерции тела относительно осей z и x.

Подставляя эти значения в выражение, определяющее L_x, получаем формулы для вычисления кинетических моментов тела, совершающего сферическое движение относительно оси х, и по аналогии относительно осей y и z:

(6.5)

Если за оси координат приняты главные оси инерции в неподвижной т.О, то центробежные моменты инерции тела относительно этих осей равны нулю, то есть

Тогда уравнения (6.5) принимают вид

(6.6)

2. Дифференциальные уравнения сферического движения твёрдого тела (динамические уравнения Эйлера)

При сферическом движении твёрдого тела его кинетический момент L_o относительно неподвижной точки О изменяется согласно уравнению

(6.7)

Свяжем с движущимся телом подвижные оси координат Ох₁y₁z₁, обозначив орты этих осей

Разложим вектор L_o на составляющие, имеющие направление осей х₁, у_1, z_1.

Рисунок 6.2

Определим производную , учитывая, что орты - переменные векторы.

(а)

Производные единичных ортов по времени можно выразить по формулам из кинематики

Пользуясь этими формулами, преобразуем первую сумму в правой части равенства (а)

Подставим это выражение в равенство (а)

Если сгруппировать члены полученного выражения по единичным ортам , где множители при ортах представляют собой проекции вектора на подвижные оси координат , и воспользоваться уравнением (6.7), получим

(6.8)

Если за подвижные оси координат приняты главные оси инерции тела в т. О, то кинетические моменты тела относительно этих осей определяются по формулам (6.6) и тогда окончательно

(6.9)

где – моменты инерции тела относительно его главных осей инерции в т.О;

- главные моменты внешних сил, приложенных к телу, относительно этих осей;

- проекции вектора угловой скорости тела ω на оси Их можно определить:

где - углы Эйлера.

Дифференциальные уравнения (6.9) сферического движения твёрдого тела называются динамическими уравнениями Эйлера. Интегрирование этих уравнений связано с большими трудностями. Поэтому рассматриваются только частные случаи сферического движения.

3. Дифференциальные уравнения движения свободного твёрдого тела.

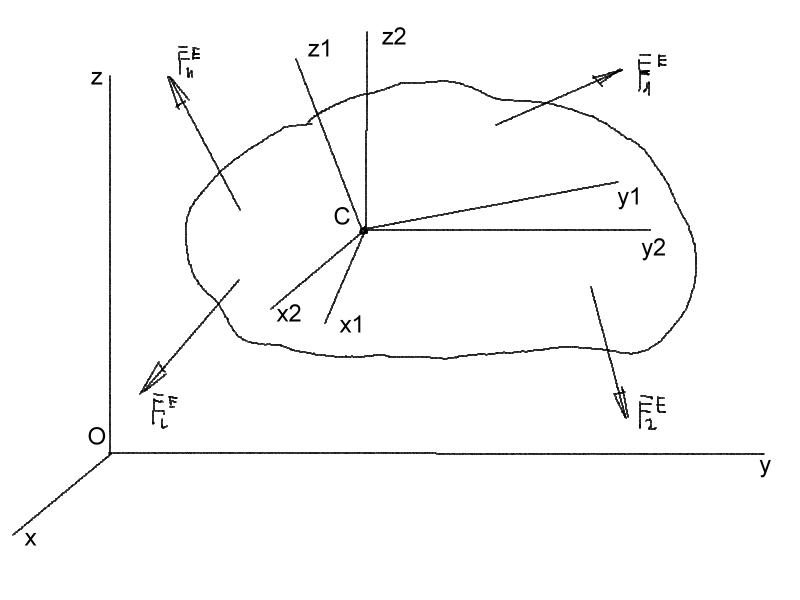
Движение свободного твёрдого тела можно рассматривать как совокупность двух его движений: поступательного вместе с центром масс и сферического вокруг центра масс.

Рассмотрим свободное тело, движущееся под действием внешних сил . Оси Cx₁y₁z₁ неизменно связанные с движущимся телом направлены по главным центральным осям инерции тела. Оси Cx₂y₂z₂ – движутся поступательно относительно неподвижной системы Оxyz.

Рисунок 6.3

Дифференциальные уравнения поступательного движения тела вместе с центром масс получаются на основе теоремы о движении центра масс механической системы:

;

; (6.10)

;

Сферическое движение твёрдого тела вокруг центра масс представляет собой движение тела относительно системы осей Cx₂y₂z_2. Это движение определяется динамическими уравнениями Эйлера.

;

; (6.11)

.

Уравнения (6.10) и (6.11) составляют шесть дифференциальных уравнений движения свободного твёрдого тела.

В результате интегрирования этих уравнений получим шесть уравнений движения свободного твёрдого тела.

(6.12)

4. Понятие о гироскопе. Гироскоп с тремя степенями свободы.

(1-й случай: центр тяжести совпадает с точкой опоры)

Гироскопом с тремя степенями свободы называется гироскоп, движение которого ограничено наличием только одной неподвижной точки.

Неподвижный гироскоп вращается равноускоренно под действием момента и в течение промежутка времени  угловая скорость вращения гироскопа вокруг оси Сх возрастает от 0 до ₁. После прекращения действия силы F гироскоп продолжает вращаться по инерции вокруг оси Сх с постоянной угловой скоростью ₁.

Рисунок 82

Вращающийся гироскоп (вокруг оси Cz₁). Его кинетический момент направлен вдоль оси симметрии гироскопа Сz₁ и равен

Где - угловая скорость собственного вращения гироскопа.

По теореме Резаля скорость конца вектора кинетического момента гироскопа относительно неподвижной очки С геометрически равна главному моменту внешних сил, приложенных к гироскопу относительно той же точки

, где

, то есть сила F//Cy вызывает перемещение оси Cz₁ вдоль оси Сx, то есть вокруг оси Сy, а не вокруг оси Сx, как в случае с неподвижным гироскопом.

Выводы:

1. Смещение оси быстро вращающегося гироскопа происходит не по направлению силы, а по направлению её момента, т.е. перпендикулярно к направлению силы.

2. Быстрое вращение сообщает гироскопу способность противодействовать силам, стремящимся изменить направление его вращения.

Случай регулярной процессии.

(2-й случай: центр тяжести не совпадает с точкой опоры)

на волчок действуют внешние силы G, реакция опоры в т.О.

(d=OC)

zOz₁, и направлен на линии узлов ОК.

ось симметрии волчка Оz₁ вращается вокруг неподвижной оси Оz с некоторой угловой скоростью (– скорость прецессии, – угол прецессии).

Рисунок 83

Определим угловую скорость прецессии . По теореме Резаля

С другой стороны

, где

таким образом,

Вывод: угловая скорость прецессии ω тем меньше, чем больше ω₁ – угловая скорость вращения волчка вокруг его оси симметрии.