Контрольные / sopromat ЭТЗ прикладная механика

ȼȼȿȾȿɇɂȿ

ɋɨɩɪɨɬɢɜɥɟɧɢɟ ɦɚɬɟɪɢɚɥɨɜ – ɩɪɚɤɬɢɱɟɫɤɢ ɩɟɪɜɚɹ ɭɱɟɛɧɚɹ ɞɢɫɰɢɩɥɢɧɚ ɨɛɳɟɢɧɠɟɧɟɪɧɨɣ ɩɨɞɝɨɬɨɜɤɢ, ɫ ɤɨɬɨɪɨɣ ɫɬɚɥɤɢɜɚɟɬɫɹ ɫɬɭɞɟɧɬ. ɗɬɨ ɧɚɭɤɚ ɨ ɩɪɨɱɧɨɫɬɢ ɢ ɠɟɫɬɤɨɫɬɢ ɷɥɟɦɟɧɬɨɜ ɢ ɞɟɬɚɥɟɣ ɤɨɧɫɬɪɭɤɰɢɣ, ɤɨɬɨɪɚɹ ɫɬɚɜɢɬ ɡɚɞɚɱɭ ɪɚɡɪɚɛɨɬɚɬɶ ɩɪɨɫɬɵɟ, ɭɞɨɛɧɵɟ ɞɥɹ ɩɪɚɤɬɢɱɟɫɤɨɝɨ ɩɪɢɦɟɧɟɧɢɹ ɦɟɬɨɞɵ ɪɚɫɱɟɬɨɜ ɬɢɩɢɱɧɵɯ, ɧɚɢɛɨɥɟɟ ɱɚɫɬɨ ɜɫɬɪɟɱɚɸɳɢɯɫɹ ɷɥɟɦɟɧɬɨɜ ɤɨɧɫɬɪɭɤɰɢɣ. ɉɪɢɦɟɧɟɧɢɟ ɭɩɪɨɳɚɸɳɢɯ ɝɢɩɨɬɟɡ ɩɨɡɜɨɥɹɟɬ ɫ ɞɨɫɬɚɬɨɱɧɨɣ ɞɥɹ ɢɧɠɟɧɟɪɧɵɯ ɰɟɥɟɣ ɬɨɱɧɨɫɬɶɸ ɜɵɩɨɥɧɹɬɶ ɩɪɨɱɧɨɫɬɧɨɣ ɪɚɫɱɟɬ ɢɡɞɟɥɢɣ, ɞɨɜɨɞɹ ɟɝɨ ɞɨ ɨɤɨɧɱɚɬɟɥɶɧɨɝɨ ɱɢɫɥɨɜɨɝɨ ɪɟɡɭɥɶɬɚɬɚ. Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ, ɧɚɭɤɚ «ɋɨɩɪɨɬɢɜɥɟɧɢɟ ɦɚɬɟɪɢɚɥɨɜ» ɫɨɡɞɚɟɬ ɨɫɧɨɜɵ ɪɚɫɱɟɬɨɜ ɷɥɟɦɟɧɬɨɜ ɤɨɧɫɬɪɭɤɰɢɣ ɧɚ ɩɪɨɱɧɨɫɬɶ.

ȼɵɜɨɞɵ, ɩɨɥɭɱɟɧɧɵɟ ɜ ɫɨɩɪɨɬɢɜɥɟɧɢɢ ɦɚɬɟɪɢɚɥɨɜ, ɜ ɞɚɥɶɧɟɣɲɟɦ ɢɫɩɨɥɶɡɭɸɬɫɹ ɜɨ ɦɧɨɝɢɯ ɫɩɟɰɢɚɥɶɧɵɯ ɬɟɯɧɢɱɟɫɤɢɯ ɞɢɫɰɢɩɥɢɧɚɯ. Ȼɟɡ ɡɧɚɧɢɹ ɢ ɩɪɢɦɟɧɟɧɢɹ ɷɬɢɯ ɜɵɜɨɞɨɜ ɧɟɥɶɡɹ ɫɩɪɨɟɤɬɢɪɨɜɚɬɶ ɢ ɩɨɫɬɪɨɢɬɶ ɧɢ ɨɞɧɨɝɨ ɫɨɨɪɭɠɟɧɢɹ, ɨɬɜɟɱɚɸɳɟɝɨ ɫɨɜɪɟɦɟɧɧɵɦ ɬɪɟɛɨɜɚɧɢɹɦ. Ɉɬɫɸɞɚ ɫɬɚɧɨɜɢɬɫɹ ɩɨɧɹɬɧɵɦ ɡɧɚɱɟɧɢɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɦɚɬɟɪɢɚɥɨɜ ɤɚɤ ɧɚɭɤɢ ɢ ɟɟ ɦɟɫɬɨ ɫɪɟɞɢ ɫɩɟɰɢɚɥɶɧɵɯ ɬɟɯɧɢɱɟɫɤɢɯ ɞɢɫɰɢɩɥɢɧ, ɜ ɤɨɬɨɪɵɯ ɩɪɚɤɬɢɱɟɫɤɢɟ ɪɚɫɱɟɬɵ ɛɚɡɢɪɭɸɬɫɹ ɧɚ ɜɵɜɨɞɚɯ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɦɚɬɟɪɢɚɥɨɜ.

ȼɭɫɥɨɜɢɹɯ ɩɨɫɬɨɹɧɧɨ ɫɨɤɪɚɳɚɸɳɟɝɨɫɹ ɜ ɭɱɟɛɧɵɯ ɩɥɚɧɚɯ ɜɪɟɦɟɧɢ, ɨɬɜɨɞɢɦɨɝɨ ɧɚ ɢɡɭɱɟɧɢɟ ɨɛɳɟɬɟɯɧɢɱɟɫɤɢɯ ɞɢɫɰɢɩɥɢɧ, ɢ ɜ ɬɨ ɠɟ ɜɪɟɦɹ ɧɟɨɛɯɨɞɢɦɨɫɬɢ ɮɨɪɦɢɪɨɜɚɧɢɹ ɭ ɛɭɞɭɳɢɯ ɢɧɠɟɧɟɪɨɜ ɛɚɡɨɜɨɝɨ ɨɛɴɟɦɚ ɡɧɚɧɢɣ

ɨɩɪɨɱɧɨɫɬɢ ɢ ɧɚɞɟɠɧɨɫɬɢ ɫɨɡɞɚɜɚɟɦɵɯ ɢ ɧɚɯɨɞɹɳɢɯɫɹ ɜ ɷɤɫɩɥɭɚɬɚɰɢɢ ɢɡɞɟɥɢɣ, ɜɚɠɧɨ ɢɦɟɬɶ ɨɛɟɫɩɟɱɟɧɢɟ ɫɬɭɞɟɧɬɨɜ ɩɨɫɨɛɢɹɦɢ, ɧɟɛɨɥɶɲɢɦɢ ɩɨ ɨɛɴɟɦɭ, ɧɨ ɨɯɜɚɬɵɜɚɸɳɢɦɢ ɧɟɨɛɯɨɞɢɦɵɟ ɪɚɡɞɟɥɵ ɡɧɚɧɢɣ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɡɚɞɚɱɚɦɢ ɮɨɪɦɢɪɨɜɚɧɢɹ ɭ ɫɬɭɞɟɧɬɨɜ ɧɟɨɛɯɨɞɢɦɨɣ ɩɨɞɝɨɬɨɜɤɢ ɩɨ ɩɪɨɱɧɨɫɬɢ ɢ ɧɚɞɟɠɧɨɫɬɢ ɤɨɧɫɬɪɭɤɰɢɣ.

ɇɚɫɬɨɹɳɟɟ ɩɨɫɨɛɢɟ ɩɪɟɞɧɚɡɧɚɱɟɧɨ ɩɪɟɢɦɭɳɟɫɬɜɟɧɧɨ ɞɥɹ ɫɬɭɞɟɧɬɨɜ, ɨɛɭɱɚɸɳɢɯɫɹ ɩɨ ɛɟɡɨɬɪɵɜɧɨɣ ɮɨɪɦɟ ɨɛɭɱɟɧɢɹ ɞɥɹ ɧɟɦɟɯɚɧɢɱɟɫɤɢɯ ɫɩɟɰɢɚɥɶɧɨɫɬɟɣ, ɜɤɥɸɱɚɸɳɟɣ ɜ ɫɟɛɹ ɤɭɪɫ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɦɚɬɟɪɢɚɥɨɜ ɩɨ ɫɨɤɪɚɳɟɧɧɨɣ ɩɪɨɝɪɚɦɦɟ ɢɥɢ ɜɯɨɞɹɳɟɣ ɜ ɫɨɫɬɚɜ ɤɭɪɫɚ "ɉɪɢɤɥɚɞɧɚɹ ɦɟɯɚɧɢɤɚ". ɗɬɨ ɩɨɫɨɛɢɟ ɫɨɞɟɪɠɢɬ ɨɫɧɨɜɧɨɣ ɦɚɬɟɪɢɚɥ ɩɨ ɢɡɭɱɚɟɦɨɣ ɞɢɫɰɢɩɥɢɧɟ.

ȼɨɫɧɨɜɧɵɟ ɪɚɡɞɟɥɵ ɤɭɪɫɚ ɜɤɥɸɱɟɧɵ ɩɪɢɦɟɪɵ, ɩɨɡɜɨɥɹɸɳɢɟ ɨɬ ɩɪɨɫɬɟɣɲɢɯ ɡɚɞɚɱ ɩɟɪɟɯɨɞɢɬɶ ɧɚ ɛɨɥɟɟ ɫɥɨɠɧɵɟ ɩɚɪɚɥɥɟɥɶɧɨ ɫ ɢɡɭɱɟɧɢɟɦ ɬɟɨɪɟɬɢɱɟɫɤɨɝɨ ɦɚɬɟɪɢɚɥɚ. ɉɪɢɥɨɠɟɧɢɟɦ ɤ ɢɡɭɱɚɟɦɨɦɭ ɦɚɬɟɪɢɚɥɭ ɩɪɟɞɥɚɝɚɸɬɫɹ ɞɜɟ ɤɨɧɬɪɨɥɶɧɵɟ ɪɚɛɨɬɵ ɫ ɦɟɬɨɞɢɱɟɫɤɢɦɢ ɭɤɚɡɚɧɢɹɦɢ ɩɨ ɢɯ ɜɵɩɨɥɧɟɧɢɸ. ȼ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɫɩɟɰɢɚɥɶɧɨɫɬɢ ɩɪɟɩɨɞɚɜɚɬɟɥɶ ɦɨɠɟɬ ɜɚɪɶɢɪɨɜɚɬɶ ɨɛɴɟɦ ɤɨɧɬɪɨɥɶɧɵɯ ɡɚɞɚɧɢɣ.

3

1.ɈɋɇɈȼɇɕȿ ɉɈɅɈɀȿɇɂə

1.1.Ɉɛɳɢɟ ɨɩɪɟɞɟɥɟɧɢɹ ɢ ɞɨɩɭɳɟɧɢɹ

ɍɱɟɛɧɚɹ ɞɢɫɰɢɩɥɢɧɚ “ɋɨɩɪɨɬɢɜɥɟɧɢɟ ɦɚɬɟɪɢɚɥɨɜ” ɫɬɚɜɢɬ ɨɫɧɨɜɧɨɣ ɡɚɞɚɱɟɣ ɩɪɨɬɢɜɨɩɨɫɬɚɜɢɬɶ ɞɟɣɫɬɜɢɸ ɜɧɟɲɧɢɯ ɫɢɥ ɧɚ ɬɟɥɨ ɦɚɬɟɪɢɚɥ ɧɭɠɧɨɝɨ ɤɚɱɟɫɬɜɚ ɢ ɜ ɧɟɨɛɯɨɞɢɦɨɦ ɤɨɥɢɱɟɫɬɜɟ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɞɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɩɪɨɱɧɨɫɬɢ ɢɡɞɟɥɢɹ ɧɟɨɛɯɨɞɢɦɨ ɭɱɢɬɵɜɚɬɶ ɬɪɢ ɨɫɧɨɜɧɵɯ ɮɚɤɬɨɪɚ: ɜɧɟɲɧɢɟ ɫɢɥɵ, ɦɚɬɟɪɢɚɥ ɢ ɝɟɨɦɟɬɪɢɸ ɬɟɥɚ, ɬ. ɟ. ɟɝɨ ɮɨɪɦɭ ɢ ɪɚɡɦɟɪɵ. ɍɱɢɬɵɜɚɹ ɦɧɨɝɨɨɛɪɚɡɢɟ ɢ ɫɥɨɠɧɨɫɬɶ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɜ ɪɟɚɥɶɧɨɫɬɢ ɨɬɦɟɱɟɧɧɵɯ ɮɚɤɬɨɪɨɜ, ɜ ɫɨɩɪɨɬɢɜɥɟɧɢɢ ɦɚɬɟɪɢɚɥɨɜ ɪɟɚɥɶɧɚɹ ɤɨɧɫɬɪɭɤɰɢɹ, ɦɚɬɟɪɢɚɥ ɢ ɞɟɣɫɬɜɭɸɳɢɟ ɫɢɥɵ ɭɩɪɨɳɚɸɬɫɹ, ɤɥɚɫɫɢɮɢɰɢɪɭɸɬɫɹ ɢ ɧɚ ɨɫɧɨɜɚɧɢɢ ɩɪɨɜɟɞɟɧɢɹ ɭɩɪɨɳɟɧɢɣ ɨɬ ɪɟɚɥɶɧɨɣ ɤɨɧɫɬɪɭɤɰɢɢ ɩɟɪɟɯɨɞɹɬ ɤ ɚɧɚɥɢɡɭ ɪɚɫɱɟɬɧɨɣ ɫɯɟɦɵ. Ɋɚɫɫɦɨɬɪɢɦ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨ ɷɬɢ ɭɩɪɨɳɟɧɢɹ.

Ɇɚɬɟɪɢɚɥ, ɢɫɩɨɥɶɡɭɟɦɵɣ ɜ ɤɨɧɫɬɪɭɤɰɢɹɯ, ɫɱɢɬɚɸɬ ɢɞɟɚɥɶɧɨ ɭɩɪɭɝɢɦ, ɬ. ɟ. ɩɨɞɱɢɧɹɸɳɢɦɫɹ ɩɪɢ ɧɚɝɪɭɠɟɧɢɢ ɡɚɤɨɧɭ Ƚɭɤɚ. ɉɪɢɧɢɦɚɟɬɫɹ ɝɢɩɨɬɟɡɚ ɨ ɫɩɥɨɲɧɨɫɬɢ ɢ ɨɞɧɨɪɨɞɧɨɫɬɢ ɦɚɬɟɪɢɚɥɚ, ɬ. ɟ. ɨɛ ɨɬɫɭɬɫɬɜɢɢ ɩɭɫɬɨɬ ɢ ɪɚɡɪɵɜɨɜ, ɢ ɨ ɧɟɢɡɦɟɧɧɨɫɬɢ ɫɜɨɣɫɬɜ ɩɨ ɜɫɟɦɭ ɟɝɨ ɨɛɴɟɦɭ. Ɇɚɬɟɪɢɚɥ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ ɢɡɨɬɪɨɩɧɵɦ, ɬ. ɟ. ɨɛɥɚɞɚɸɳɢɦ ɨɞɢɧɚɤɨɜɵɦɢ ɦɟɯɚɧɢɱɟɫɤɢɦɢ ɫɜɨɣɫɬɜɚɦɢ ɩɨ ɜɫɟɦ ɧɚɩɪɚɜɥɟɧɢɹɦ.

Ⱦɟɣɫɬɜɭɸɳɢɟ ɧɚ ɬɟɥɨ ɜɧɟɲɧɢɟ ɫɢɥɵ ɤɥɚɫɫɢɮɢɰɢɪɭɸɬ ɩɨ ɪɚɡɧɵɦ ɩɪɢɡɧɚɤɚɦ: ɩɨ ɨɛɥɚɫɬɢ ɞɟɣɫɬɜɢɹ – ɫɨɫɪɟɞɨɬɨɱɟɧɧɵɟ, ɬ. ɟ. ɞɟɣɫɬɜɭɸɳɢɟ ɜ ɬɨɱɤɟ, ɨɛɨɡɧɚɱɚɸɬ “F” ɢ ɩɪɟɞɩɨɥɚɝɚɸɬ, ɱɬɨ ɢɯ ɞɟɣɫɬɜɢɟ ɫɨɫɪɟɞɨɬɨɱɟɧɨ ɜ ɬɨɱɤɟ, ɚ ɪɚɡɦɟɪɧɨɫɬɶ ɇ ɢɥɢ ɤɝɫ; ɪɚɫɩɪɟɞɟɥɟɧɧɵɟ ɩɨ ɞɥɢɧɟ – q (ɇ/ɦ ɢɥɢ ɤɝɫ/ɦ); ɪɚɫɩɪɟɞɟɥɟɧɧɵɟ ɩɨ ɩɥɨɳɚɞɢ “s” (ɇ/ɦ2 ɢɥɢ ɤɝɫ/ɦ2); ɪɚɫɩɪɟɞɟɥɟɧɧɵɟ ɩɨ ɨɛɴɟɦɭ “k ” (ɇ/ɦ3 ɢɥɢ ɤɝɫ/ɦ3); ɩɨ ɜɪɟɦɟɧɢ ɞɟɣɫɬɜɢɹ – ɩɨɫɬɨɹɧɧɨ ɞɟɣɫɬɜɭɸɳɢɟ ɢ ɫɬɚɬɢɱɟɫɤɢɟ, ɰɢɤɥɢɱɟɫɤɢɟ ɢ ɞɢɧɚɦɢɱɟɫɤɢɟ (ɭɞɚɪɧɵɟ). Ʉ ɫɨɫɪɟɞɨɬɨɱɟɧɧɵɦ ɫɢɥɚɦ ɨɬɧɨɫɹɬɫɹ ɧɚɝɪɭɡɤɢ ɜ ɜɢɞɟ ɩɚɪ ɫɢɥ (ɦɨɦɟɧɬɨɜ ɫɢɥ)

– “Ɇ” ɢɥɢ “Ɍ” (H ɦ).

ɋɢɥɵ ɪɚɡɥɢɱɚɸɬ ɜɧɟɲɧɢɟ ɢ ɜɧɭɬɪɟɧɧɢɟ. ȼɧɟɲɧɢɟ – ɷɬɨ ɫɢɥɵ, ɩɪɢɥɨɠɟɧɧɵɟ ɢɡɜɧɟ ɤ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɦɭ ɨɛɴɟɤɬɭ. Ʉ ɜɧɟɲɧɢɦ ɫɢɥɚɦ ɨɬɧɨɫɹɬɫɹ ɢ ɪɟɚɤɰɢɢ. ȼɧɭɬɪɟɧɧɢɟ – ɷɬɨ ɫɢɥɵ ɫɰɟɩɥɟɧɢɹ ɱɚɫɬɢɱɟɤ ɬɟɥɚ ɢɥɢ ɟɝɨ ɷɥɟɦɟɧɬɨɜ ɜɧɭɬɪɢ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɝɨ ɨɛɴɟɤɬɚ.

ɉɪɢ ɨɰɟɧɤɟ ɞɟɣɫɬɜɢɹ ɫɢɥ ɧɚ ɭɩɪɭɝɨɟ ɬɟɥɨ ɩɪɢɦɟɧɹɟɬɫɹ ɩɪɢɧɰɢɩ ɧɟɡɚɜɢɫɢɦɨɫɬɢ ɞɟɣɫɬɜɢɹ ɫɢɥ, ɡɚɤɥɸɱɚɸɳɢɣɫɹ ɜ ɬɨɦ, ɱɬɨ ɪɟɡɭɥɶɬɚɬ ɞɟɣɫɬɜɢɹ ɫɢɫɬɟɦɵ ɫɢɥ ɧɚ ɬɟɥɨ ɪɚɜɟɧ ɫɭɦɦɟ ɪɟɡɭɥɶɬɚɬɨɜ ɞɟɣɫɬɜɢɹ ɤɚɠɞɨɣ ɫɢɥɵ ɜ ɨɬɞɟɥɶɧɨɫɬɢ ɧɟɡɚɜɢɫɢɦɨ ɨɬ ɨɱɟɪɟɞɧɨɫɬɢ ɢɯ ɩɪɢɥɨɠɟɧɢɹ ɤ ɬɟɥɭ.

ɂ, ɧɚɤɨɧɟɰ, ɪɚɡɦɟɪɵ ɢ ɮɨɪɦɚ ɬɟɥɚ, ɬ. ɟ. ɝɟɨɦɟɬɪɢɹ ɬɟɥɚ. ȼ ɫɨɩɪɨɬɢɜɥɟɧɢɢ ɦɚɬɟɪɢɚɥɨɜ ɨɫɧɨɜɧɵɦ ɷɥɟɦɟɧɬɨɦ ɹɜɥɹɟɬɫɹ ɫɬɟɪɠɟɧɶ (ɛɪɭɫ), ɬ. ɟ. ɬɟɥɨ, ɬɨɥɳɢɧɚ ɢ ɲɢɪɢɧɚ ɤɨɬɨɪɨɝɨ ɧɟɫɨɢɡɦɟɪɢɦɨ ɦɟɧɶɲɟ ɟɝɨ ɞɥɢɧɵ. ȿɫɥɢ ɞɜɚ ɢɡɦɟɪɟɧɢɹ – ɞɥɢɧɚ ɢ ɲɢɪɢɧɚ – ɦɧɨɝɨ ɛɨɥɶɲɟ ɬɨɥɳɢɧɵ, ɬɨ ɬɚɤɨɟ ɬɟɥɨ ɧɚɡɵɜɚɟɬɫɹ ɩɥɚɫɬɢɧɨɣ. ȿɫɥɢ ɩɨɜɟɪɯɧɨɫɬɢ ɩɥɚɫɬɢɧɵ ɤɪɢɜɨɥɢɧɟɣɧɵɟ, ɬɨ ɷɬɨ

– ɨɛɨɥɨɱɤɚ. Ⱥ ɟɫɥɢ ɜɫɟ ɬɪɢ ɢɡɦɟɪɟɧɢɹ ɨɞɧɨɝɨ ɩɨɪɹɞɤɚ, ɬɨ ɬɚɤɨɟ ɬɟɥɨ ɧɚɡɵɜɚɸɬ ɦɚɫɫɢɜɧɵɦ ɬɟɥɨɦ.

4

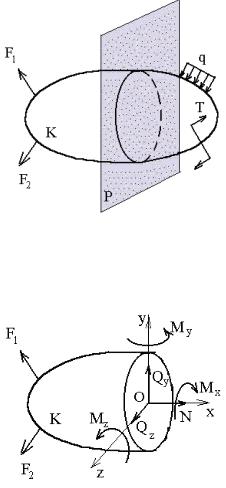
1.2. ȼɧɭɬɪɟɧɧɢɟ ɫɢɥɨɜɵɟ ɮɚɤɬɨɪɵ. Ɇɟɬɨɞ ɫɟɱɟɧɢɣ

Ɉɞɧɨɣ ɢɡ ɜɚɠɧɟɣɲɢɯ ɡɚɞɚɱ ɜ ɫɨɩɪɨɬɢɜɥɟɧɢɢ ɦɚɬɟɪɢɚɥɨɜ ɹɜɥɹɟɬɫɹ ɨɩɪɟɞɟɥɟɧɢɟ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ (ɭɫɢɥɢɣ). Ⱦɥɹ ɢɯ ɧɚɯɨɠɞɟɧɢɹ ɢɫɩɨɥɶɡɭɸɬ ɦɟɬɨɞ ɫɟɱɟɧɢɣ. Ɋɚɫɫɦɨɬɪɢɦ ɩɪɢɦɟɧɟɧɢɟ ɷɬɨɝɨ ɦɟɬɨɞɚ ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ɧɚɝɪɭɠɟɧɢɹ. ɉɭɫɬɶ ɬɟɥɨ Ʉ ɡɚɝɪɭɠɟɧɨ ɜɧɟɲɧɢɦɢ ɫɢɥɚɦɢ F, q, T (ɪɢɫ. 1.1). ɇɟɨɛɯɨɞɢɦɨ ɧɚɣɬɢ ɜɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ ɜ ɩɥɨɫɤɨɫɬɢ ɬɟɥɚ, ɩɨɥɭɱɚɸɳɟɣɫɹ ɜ ɪɟɡɭɥɶɬɚɬɟ ɟɝɨ ɩɟɪɟɫɟɱɟɧɢɹ ɩɥɨɫɤɨɫɬɶɸ Ɋ. Ɍɟɥɨ ɧɚɯɨɞɢɬɫɹ ɜ ɪɚɜɧɨɜɟɫɢɢ, ɨɧɨ ɧɟɩɨɞɜɢɠɧɨ.

Ɂɞɟɫɶ ɜɧɭɬɪɟɧɧɢɟ ɫɢɥɨɜɵɟ ɮɚɤɬɨɪɵ ɢɦɟɸɬ ɫɥɟɞɭɸɳɢɟ ɧɚɡɜɚɧɢɹ: N – ɩɪɨɞɨɥɶɧɚɹ (ɪɟɠɟ – ɧɨɪɦɚɥɶɧɚɹ) ɫɢɥɚ; Qy ɢ Qz – ɩɨɩɟɪɟɱɧɵɟ (ɩɟɪɟɪɟɡɵɜɚɸɳɢɟ) ɫɢɥɵ ɜ ɧɚɩɪɚɜɥɟɧɢɢ, ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ, ɨɫɟɣ ɭ ɢ z; Ɇɯ ɢɥɢ Mɤ – ɤɪɭɬɹɳɢɣ ɦɨɦɟɧɬ; My ɢ Mz – ɢɡɝɢɛɚɸɳɢɟ ɦɨɦɟɧɬɵ ɨɬɧɨɫɢɬɟɥɶɧɨ ɨɫɟɣ ɭ ɢ z.

5

ɉɪɚɜɵɟ ɱɚɫɬɢ ɜɵɪɚɠɟɧɢɣ (1.1) ɩɪɟɞɫɬɚɜɥɹɸɬ ɫɨɛɨɣ: ¦Fi,x – ɫɭɦɦɚ ɩɪɨɟɤ-

ɰɢɣ ɜɫɟɯ ɜɧɟɲɧɢɯ ɫɢɥ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɨɬɫɟɱɟɧɧɭɸ ɱɚɫɬɶ, ɧɚ ɧɨɪɦɚɥɶ ɤ ɩɥɨɫɤɨɫɬɢ ɫɟɱɟɧɢɹ, ɬ. ɟ. ɧɚ ɨɫɶ ɯ; ¦Fi,y ɢ ¦Fi,z – ɫɭɦɦɚ ɩɪɨɟɤɰɢɣ ɜɫɟɯ ɜɧɟɲɧɢɯ ɫɢɥ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɨɬɫɟɱɟɧɧɭɸ ɱɚɫɬɶ, ɧɚ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɨɫɢ ɭ ɢ z; ¦Tx,F – ɫɭɦɦɚ ɦɨɦɟɧɬɨɜ ɜɫɟɯ ɜɧɟɲɧɢɯ ɫɢɥ, ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɨɬɫɟɱɟɧɧɭɸ ɱɚɫɬɶ, ɨɬɧɨɫɢɬɟɥɶɧɨ ɝɟɨɦɟɬɪɢɱɟɫɤɨɣ ɨɫɢ ɯ; ¦My,F ɢ ¦Mz,F – ɫɭɦɦɚ ɦɨɦɟɧɬɨɜ ɜɫɟɯɜɧɟɲɧɢɯɫɢɥ, ɞɟɣɫɬɜɭɸɳɢɯɧɚɨɬɫɟɱɟɧɧɭɸɱɚɫɬɶ, ɨɬɧɨɫɢɬɟɥɶɧɨɨɫɟɣɭɢz.

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɨɠɧɨ ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɪɚɜɢɥɨ ɨɩɪɟɞɟɥɟɧɢɹ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ: ɜɧɭɬɪɟɧɧɢɟ ɫɢɥɵ N, Qy ɢ Qz ɱɢɫɥɟɧɧɨ ɪɚɜɧɵ ɚɥɝɟɛɪɚɢɱɟɫɤɨɣ ɫɭɦɦɟ ɩɪɨɟɤɰɢɣ ɜɫɟɯ ɜɧɟɲɧɢɯ ɫɢɥ (ɜ ɬɨɦ ɱɢɫɥɟ ɢ ɪɟɚɤɰɢɣ), ɞɟɣɫɬɜɭɸɳɢɯ ɧɚ ɨɬɫɟɱɟɧɧɭɸ ɱɚɫɬɶ ɬɟɥɚ, ɬ. ɟ. ɩɨ ɨɞɧɭ ɫɬɨɪɨɧɭ ɫɟɱɟɧɢɹ, ɧɚ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ ɨɫɢ ɯ, ɭ ɢɥɢ z. Ⱥɧɚɥɨɝɢɱɧɨ, ɢɡ ɬɪɟɯ ɩɨɫɥɟɞɧɢɯ ɫɬɪɨɱɟɤ ɜɵɪɚɠɟɧɢɹ (1.1) ɫɥɟɞɭɟɬ: ɡɧɚɱɟɧɢɟ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ Ɇɯ, My ɢ Mz ɱɢɫɥɟɧɧɨ ɪɚɜɧɨ ɚɥɝɟɛɪɚɢɱɟɫɤɨɣ ɫɭɦɦɟ ɦɨɦɟɧɬɨɜ ɜɧɟɲɧɢɯ ɫɢɥ,

ɞɟɣɫɬɜɭɸɳɢɯ ɩɨ ɨɞɧɭ ɫɬɨɪɨɧɭ ɫɟɱɟɧɢɹ, ɨɬɧɨɫɢɬɟɥɶɧɨ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɨɫɟɣ ɯ, ɭ ɢ z.

ɗɬɢ ɠɟ ɡɧɚɱɟɧɢɹ ɜɧɭɬɪɟɧɧɢɯ ɭɫɢɥɢɣ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ, ɪɚɫɫɦɚɬɪɢɜɚɹ ɪɚɜɧɨɜɟɫɢɟ ɩɪɚɜɨɣ ɱɚɫɬɢ [ɩɨɩɪɨɛɭɣɬɟ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨ ɢɡɨɛɪɚɡɢɬɶ ɩɪɚɜɭɸ ɱɚɫɬɶ ɫ ɨɛɨɡɧɚɱɟɧɢɟɦ ɜɫɟɯ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ ɢ ɜɧɟɲɧɢɯ ɫɢɥ ɢ ɡɚɩɢɫɚɬɶ ɜɵɪɚɠɟɧɢɟ, ɚɧɚɥɨɝɢɱɧɨɟ (1.1)].

ɍɱɟɬ ɧɟɡɚɜɢɫɢɦɨɫɬɢ ɜɧɭɬɪɟɧɧɟɝɨ ɭɫɢɥɢɹ ɜ ɫɟɱɟɧɢɢ ɨɬ ɜɵɛɨɪɚ ɫɬɨɪɨɧɵ (ɥɟɜɨɣ, ɩɪɚɜɨɣ) ɨɬɫɟɱɟɧɧɨɣ ɱɚɫɬɢ ɩɨɡɜɨɥɹɟɬ ɜɵɛɢɪɚɬɶ ɛɨɥɟɟ ɩɪɨɫɬɨɣ ɜɚɪɢɚɧɬ ɨɩɪɟɞɟɥɟɧɢɹ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ. ɇɚɩɪɢɦɟɪ, ɟɫɥɢ ɞɥɹ ɤɨɧɤɪɟɬɧɨɣ ɫɢɫɬɟɦɵ ɦɨɠɧɨ ɜɵɛɪɚɬɶ ɨɬɫɟɱɟɧɧɭɸ ɱɚɫɬɶ, ɜ ɤɨɬɨɪɭɸ ɧɟ ɜɯɨɞɹɬ ɪɟɚɤɰɢɢ ɫɜɹɡɟɣ (ɧɚɩɪɢɦɟɪ, ɤɨɧɫɨɥɶɧɚɹ ɛɚɥɤɚ), ɬɨ ɜɧɭɬɪɟɧɧɢɟ ɫɢɥɨɜɵɟ ɮɚɤɬɨɪɵ ɦɨɠɧɨ ɧɚɯɨɞɢɬɶ ɛɟɡ ɨɩɪɟɞɟɥɟɧɢɹ ɪɟɚɤɰɢɣ.

ɇɟɨɛɯɨɞɢɦɨ ɨɬɦɟɬɢɬɶ ɨɞɧɨ ɜɚɠɧɨɟ ɨɛɫɬɨɹɬɟɥɶɫɬɜɨ. Ɉɬ ɭɪɨɜɧɹ ɩɨɧɢɦɚɧɢɹ ɢ ɭɫɜɨɟɧɢɹ ɦɟɬɨɞɚ ɫɟɱɟɧɢɣ ɡɚɜɢɫɢɬ ɭɫɩɟɲɧɨɟ ɢɡɭɱɟɧɢɟ ɜɫɟɝɨ ɤɭɪɫɚ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɦɚɬɟɪɢɚɥɨɜ. ȼɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ ɧɟɨɛɯɨɞɢɦɨ ɡɧɚɬɶ ɞɥɹ ɩɪɨɜɟɞɟɧɢɹ ɩɪɨɱɧɨɫɬɧɵɯ ɪɚɫɱɟɬɨɜ. ɉɪɢɧɢɦɚɹ ɜɨ ɜɧɢɦɚɧɢɟ ɜɚɠɧɨɫɬɶ ɷɬɨɝɨ ɪɚɡɞɟɥɚ, ɡɚɩɢɲɟɦ ɤɪɚɬɤɨ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶ ɨɫɧɨɜɧɵɯ ɲɚɝɨɜ ɩɪɢ ɩɪɢɦɟɧɟɧɢɢ ɦɟɬɨɞɚ ɫɟɱɟɧɢɹ.

ɊɊɚɫɫɟɤɚɟɦ ɬɟɥɨ ɩɥɨɫɤɨɫɬɶɸ ɧɚ ɞɜɟ ɱɚɫɬɢ.

ɈɈɬɛɪɚɫɵɜɚɟɦ ɨɞɧɭ ɢɡ ɱɚɫɬɟɣ ɬɟɥɚ.

Ɂ Ɂɚɦɟɧɹɟɦ ɞɟɣɫɬɜɢɟ ɨɬɛɪɨɲɟɧɧɨɣ ɱɚɫɬɢ ɧɚ ɨɫɬɚɜɲɭɸɫɹ ɜɧɭɬɪɟɧɧɢɦɢ ɫɢɥɨɜɵɦɢ ɮɚɤɬɨɪɚɦɢ.

ɍɍɪɚɜɧɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ ɫɨɫɬɚɜɥɹɟɦ.

ɂɬɚɤ, ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ɧɚɝɪɭɠɟɧɢɹ ɜ ɩɨɩɟɪɟɱɧɨɦ ɫɟɱɟɧɢɢ ɦɨɝɭɬ ɞɟɣɫɬɜɨɜɚɬɶ ɲɟɫɬɶ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ. ȼɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ, ɜɨɡɧɢɤɚɸɳɢɟ ɜ ɫɟɱɟɧɢɢ ɛɪɭɫɚ, ɨɩɪɟɞɟɥɹɸɬ ɜɢɞ ɧɚɝɪɭɠɟɧɢɹ (ɞɟɮɨɪɦɚɰɢɢ). ȿɫɥɢ

6

ɞɟɣɫɬɜɭɟɬ ɬɨɥɶɤɨ ɨɞɧɨ ɜɧɭɬɪɟɧɧɟɟ ɭɫɢɥɢɟ, ɬɨ ɬɚɤɨɣ ɜɢɞ ɧɚɝɪɭɠɟɧɢɹ (ɢ ɞɟɮɨɪɦɚɰɢɢ) ɧɚɡɵɜɚɸɬ ɩɪɨɫɬɵɦ. Ɋɚɡɥɢɱɚɸɬ ɫɥɟɞɭɸɳɢɟ ɜɢɞɵ ɧɚɝɪɭɠɟɧɢɣ ɢ ɞɟɮɨɪɦɚɰɢɣ (ɫɦ. ɬɚɛɥ.1).

ɉɪɢɦɟɪɵ ɨɩɪɟɞɟɥɟɧɢɹ ɜɧɭɬɪɟɧɧɢɯ ɭɫɢɥɢɣ ɞɥɹ ɩɪɨɫɬɵɯ ɫɯɟɦ ɧɚɝɪɭɠɟɧɢɹ ɩɪɢɜɟɞɟɧɵ ɧɢɠɟ ɜ ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɯ ɪɚɡɞɟɥɚɯ (ɪɚɫɬɹɠɟɧɢɟ – 2.1, ɫɞɜɢɝ ɢ ɤɪɭɱɟɧɢɟ – 5.1 – 5.2, ɢɡɝɢɛ – 6.1). ɋɥɟɞɭɟɬ ɧɚɱɚɬɶ ɢɡɭɱɟɧɢɟ ɷɬɨɝɨ ɦɚɬɟɪɢɚɥɚ ɢɦɟɧɧɨ ɫ ɫɚɦɵɯ ɩɪɨɫɬɵɯ ɫɯɟɦ, ɩɪɢ ɷɬɨɦ ɨɛɪɚɬɢɬɟ ɨɫɨɛɨɟ ɜɧɢɦɚɧɢɟ ɧɚ ɩɪɚɜɢɥɨ ɡɧɚɤɨɜ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ.

1.3. ɉɨɧɹɬɢɟ ɨ ɧɚɩɪɹɠɟɧɢɹɯ ɢ ɞɟɮɨɪɦɚɰɢɹɯ

ȼɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ ɜ ɫɟɱɟɧɢɢ ɩɪɟɞɫɬɚɜɥɹɸɬ ɫɨɛɨɣ ɢɧɬɟɝɪɚɥɶɧɭɸ ɜɟɥɢɱɢɧɭ ɥɨɤɚɥɶɧɵɯ (ɦɟɫɬɧɵɯ) ɭɫɢɥɢɣ, ɪɚɫɩɪɟɞɟɥɟɧɧɵɯ ɩɨ ɜɫɟɦɭ ɫɟɱɟɧɢɸ. ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ ɢɧɬɟɧɫɢɜɧɨɫɬɶ ɥɨɤɚɥɶɧɵɯ ɜɧɭɬɪɟɧɧɢɯ ɭɫɢɥɢɣ ɛɭɞɟɬ ɪɚɡɥɢɱɧɚ ɜ ɪɚɡɧɵɯ ɬɨɱɤɚɯ ɫɟɱɟɧɢɹ. ɉɨɷɬɨɦɭ ɜ ɞɚɥɶɧɟɣɲɟɦ ɭɞɨɛɧɟɟ ɨɩɟɪɢɪɨɜɚɬɶ ɩɨɧɹɬɢɟɦ ɧɚɩɪɹɠɟɧɢɹ, ɩɪɟɞɫɬɚɜɥɹɸɳɟɝɨ ɫɨɛɨɣ ɜɧɭɬɪɟɧɧɸɸ ɫɢɥɭ, ɨɬ-

ɧɟɫɟɧɧɭɸ ɤ ɟɞɢɧɢɰɟ ɩɥɨɳɚɞɢ ɜ ɞɚɧɧɨɣ ɬɨɱɤɟ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɝɨ ɫɟɱɟɧɢɹ.

ɉɭɫɬɶ ɧɚ ɷɥɟɦɟɧɬɚɪɧɭɸ ɩɥɨɳɚɞɤɭ dA (ɪɢɫ.1.3) ɞɟɣɫɬɜɭɟɬ ɜɧɭɬɪɟɧɧɟɟ ɭɫɢɥɢɟ dR, ɬɨɝɞɚ ɩɨɥɧɨɟ ɧɚɩɪɹɠɟɧɢɟ pi ɨɩɪɟɞɟɥɢɬɫɹ ɜɵɪɚɠɟɧɢɟɦ:

ȿɫɥɢ ɩɪɨɟɤɰɢɢ ɜɟɤɬɨɪɚ dR ɫɨɫɬɚɜɥɹɸɬ dN ɢ dQ,

Ɋɢɫ ɬɨ ɧɨɪɦɚɥɶɧɵɟ ɧɚɩɪɹɠɟɧɢɹ σ ɢ ɤɚɫɚɬɟɥɶɧɵɟ τ ,

. 1.3

ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ, ɡɚɩɢɲɭɬɫɹ:

7

ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ ɦɟɠɞɭ ɧɚɩɪɹɠɟɧɢɹɦɢ ɫɭɳɟɫɬɜɭɟɬ ɫɜɹɡɶ:

AC →0

Ⱥɧɚɥɨɝɢɱɧɨ ɦɨɝɭɬ ɛɵɬɶ ɡɚɩɢɫɚɧɵ ɞɟɮɨɪɦɚɰɢɢ ɫɞɜɢɝɚ ɢ ɜ ɨɫɬɚɥɶɧɵɯ ɞɜɭɯ

ɜɡɚɢɦɧɨ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɵɯ ɩɥɨɫɤɨɫɬɹɯ γɭz ɢ γɯz .

ɂɬɚɤ, ɜ ɤɭɪɫɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɦɚɬɟɪɢɚɥɨɜ ɢɡɥɚɝɚɸɬɫɹ ɧɚɢɛɨɥɟɟ ɩɪɨ- ɫɬɵɟ ɦɟɬɨɞɵ ɪɚɫɱɟɬɚ. ɉɪɢ ɷɬɨɦ ɜɜɨɞɹɬɫɹ ɭɩɪɨɳɚɸɳɢɟ ɝɢɩɨɬɟɡɵ (ɞɨɩɭ-

8

ɳɟɧɢɹ), ɩɨɡɜɨɥɹɸɳɢɟ ɪɟɚɥɶɧɭɸ ɤɨɧɫɬɪɭɤɰɢɸ ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɜɢɞɟ ɪɚɫɱɟɬ- ɧɨɣ ɫɯɟɦɵ. ɗɬɢ ɞɨɩɭɳɟɧɢɹ ɪɚɫɩɪɨɫɬɪɚɧɹɸɬɫɹ ɧɚ ɦɚɬɟɪɢɚɥ, ɧɚɝɪɭɡɤɭ ɢ ɝɟɨɦɟɬɪɢɸ ɬɟɥɚ. ȼɜɨɞɹɬɫɹ ɩɨɧɹɬɢɹ ɜɧɭɬɪɟɧɧɢɯ ɭɫɢɥɢɣ, ɨɩɪɟɞɟɥɹɟɦɵɯ ɦɟɬɨɞɨɦ ɫɟɱɟɧɢɣ ɢ ɧɚɩɪɹɠɟɧɢɣ, ɩɪɟɞɫɬɚɜɥɹɸɳɢɯ ɫɨɛɨɣ ɜɧɭɬɪɟɧɧɢɟ ɭɫɢ- ɥɢɹ, ɨɬɧɟɫɟɧɧɵɟ ɤ ɟɞɢɧɢɰɟ ɩɥɨɳɚɞɢ. ɉɨɞ ɞɟɣɫɬɜɢɟɦ ɫɢɥ ɬɨɱɤɢ ɬɟɥɚ ɩɟɪɟ- ɦɟɳɚɸɬɫɹ, ɚ ɤɨɥɢɱɟɫɬɜɟɧɧɨɣ ɦɟɪɨɣ ɷɬɢɯ ɩɟɪɟɦɟɳɟɧɢɣ ɫɥɭɠɚɬ ɞɟɮɨɪɦɚ- ɰɢɢ – ɥɢɧɟɣɧɵɟ ɢ ɭɝɥɨɜɵɟ.

2.ɊȺɋɌəɀȿɇɂȿ ɂ ɋɀȺɌɂȿ

2.1.ȼɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ, ɧɚɩɪɹɠɟɧɢɹ, ɞɟɮɨɪɦɚɰɢɢ

2.1.1.ɉɪɨɞɨɥɶɧɚɹ ɫɢɥɚ. Ɋɚɫɬɹɠɟɧɢɟ – ɩɪɨɫɬɨɣ ɜɢɞ ɧɚɝɪɭɠɟɧɢɹ, ɤɨɝɞɚ ɬɨɥɶɤɨ ɨɞɢɧ ɜɧɭɬɪɟɧɧɢɣ ɫɢɥɨɜɨɣ ɮɚɤɬɨɪ “ɩɪɨɞɨɥɶɧɚɹ ɫɢɥɚ” ɧɟ ɪɚɜɟɧ ɧɭɥɸ. Ⱦɪɭɝɢɯ ɜɧɭɬɪɟɧɧɢɯ ɭɫɢɥɢɣ ɧɟɬ. Ɋɚɫɬɹɝɢɜɚɸɳɟɟ ɜɧɭɬɪɟɧɧɟɟ ɭɫɢɥɢɟ, ɬ. ɟ. ɧɚɩɪɚɜɥɟɧɧɨɟ ɨɬ ɫɟɱɟɧɢɹ, ɫɱɢɬɚɸɬ ɩɨɥɨɠɢɬɟɥɶɧɵɦ, ɫɠɢɦɚɸɳɟɟ – ɨɬɪɢɰɚɬɟɥɶɧɵɦ. ɇɚ ɪɢc. 2.1 ɩɨɤɚɡɚɧɨ ɨɩɪɟɞɟɥɟɧɢɟ ɜɧɭɬɪɟɧɧɢɯ ɭɫɢɥɢɣ ɩɪɢ ɪɚɫɬɹɠɟɧɢɢ (ɫɠɚɬɢɢ). ɉɪɢɦɟɧɹɟɦ ɦɟɬɨɞ ɫɟɱɟɧɢɣ.

Ɋɚɫɫɟɤɚɟɦ ɫɬɟɪɠɟɧɶ ɩɥɨɫɤɨɫɬɶɸ I-I (ɪɢɫ. 2.1, ɚ), ɨɬɛɪɚɫɵɜɚɟɦ ɜɟɪɯɧɸɸ ɱɚɫɬɶ (ɜɵɲɟ I-I), ɩɪɢɤɥɚɞɵɜɚɟɦ N

ɫɟɱɟɧɢɹɯ ɩɪɢɥɨɠɟɧɨ ɧɟɫɤɨɥɶɤɨ ɫɢɥ, ɜɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ ɩɨ ɞɥɢɧɟ ɧɚ ɪɚɡɥɢɱɧɵɯ ɭɱɚɫɬɤɚɯ ɫɬɟɪɠɧɹ ɛɭɞɭɬ ɪɚɡɥɢɱɧɵɦɢ. Ⱦɥɹ ɧɚɝɥɹɞɧɨɫɬɢ ɫɬɪɨɹɬ ɝɪɚɮɢɤ ɢɡɦɟɧɟɧɢɹ N(x) ɩɨ ɞɥɢɧɟ ɫɬɟɪɠɧɹ, ɤɨɬɨɪɵɣ ɧɚɡɵɜɚɸɬ ɷɩɸɪɨɣ ɩɪɨɞɨɥɶɧɵɯ ɫɢɥ.

ɉɪɢɦɟɪ 1. ɋɬɟɪɠɟɧɶ ɧɚɯɨɞɢɬɫɹ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɫɢɥ F1=40 ɤɇ, F2=20 ɤɇ ɢ F3=60 ɤɇ, "1 = "2 = "3 = 1ɦ, Ⱥ2 = 2 Ⱥ1= 4 ɫɦ2 (ɪɢɫ. 2.2, ɚ). Ɉɩɪɟɞɟɥɢɬɶ ɜɧɭɬɪɟɧɧɢɟ ɭɫɢɥɢɹ. ɉɨɫɬɪɨɢɬɶ ɷɩɸɪɵ.

Ɋɟɲɟɧɢɟ. Ɋɚɡɛɢɜɚɟɦ ɫɬɟɪɠɟɧɶ ɧɚ ɭɱɚɫɬɤɢ, ɝɪɚɧɢɰɚɦɢ ɤɨɬɨɪɵɯ ɛɭɞɭɬ ɫɟɱɟɧɢɹ, ɜ ɤɨɬɨɪɵɯ ɩɪɢɥɨɠɟɧɵ ɫɢɥɵ. ɉɨɥɭɱɢɦ ɬɪɢ ɭɱɚɫɬɤɚ: I, II ɢ III.

Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɜɧɭɬɪɟɧɧɢɯ ɫɢɥɨɜɵɯ ɮɚɤɬɨɪɨɜ ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɦɟɬɨɞɨɦ ɫɟɱɟɧɢɣ. ɇɚ ɭɱɚɫɬɤɟ I ɩɪɨɜɟɞɟɦ ɫɟɱɟɧɢɟ 1-1 ɢ ɨɬɛɪɨɫɢɦ ɥɟɜɭɸ ɱɚɫɬɶ ɛɪɭɫɚ (ɪɢɫ. 2.2, ɛ). Ɂɚɬɟɦ ɩɪɢɥɨɠɢɦ ɤ ɫɟɱɟɧɢɸ 1-1 ɩɪɨɞɨɥɶɧɭɸ ɫɢɥɭ N1, ɡɚɦɟɧɹɸɳɭɸ ɞɟɣɫɬɜɢɟ ɨɬɛɪɨɲɟɧɧɨɣ ɱɚɫɬɢ ɫɬɟɪɠɧɹ ɧɚ ɨɫɬɚɜɲɭɸɫɹ ɩɪɚɜɭɸ ɱɚɫɬɶ. ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɪɚɜɧɟɧɢɹɦɢ (1.1) ɞɪɭɝɢɟ ɜɧɭɬɪɟɧɧɢɟ ɫɢɥɨɜɵɟ ɮɚɤɬɨɪɵ ɪɚɜɧɵ ɧɭɥɸ, ɬɚɤ ɤɚɤ ɪɚɜɧɵ ɧɭɥɸ ɩɪɚɜɵɟ ɱɚɫɬɢ ɭɪɚɜɧɟɧɢɣ ɪɚɜɟɧ-

9

ɲɬɪɢɯɨɜɤɢ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɜɟɥɢɱɢɧɵ N ɜ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɦ ɫɟɱɟɧɢɢ. Ɇɨɠɧɨ ɛɵɥɨ ɛɵ ɨɩɪɟɞɟɥɢɬɶ ɜɟɥɢɱɢɧɵ N, ɪɚɫɫɦɚɬɪɢɜɚɹ ɪɚɜɧɨɜɟɫɢɟ

ɥɟɜɨɣ ɨɬɫɟɱɟɧɧɨɣ ɱɚɫɬɢ ɛɪɭɫɚ. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɧɟɨɛɯɨɞɢɦɨ ɩɪɟɞɜɚɪɢɬɟɥɶɧɨ ɨɩɪɟɞɟɥɢɬɶ ɪɟɚɤɰɢɢ ɜ ɡɚɞɟɥɤɟ, ɱɬɨ ɭɫɥɨɠɧɢɥɨ ɛɵ ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ.

2.1.2. ɇɚɩɪɹɠɟɧɢɹ ɜ ɩɨɩɟɪɟɱɧɨɦ ɫɟɱɟɧɢɢ.

ɝɞɟ Ⱥ – ɩɥɨɳɚɞɶ ɩɨɩɟɪɟɱɧɨɝɨ ɫɟɱɟɧɢɹ.

ɂɡ ɨɩɵɬɚ ɢɡɜɟɫɬɧɨ, ɱɬɨ ɰɟɧɬɪɚɥɶɧɨ ɩɪɢɥɨɠɟɧɧɚɹ ɫɢɥɚ ɩɪɢɜɨɞɢɬ ɤ ɪɚɜɧɨɦɟɪɧɨɦɭ ɪɚɫɬɹɠɟɧɢɸ ɫɬɟɪɠɧɹ, ɚ ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɢ ɩɨɫɬɨɹɧɫɬɜɭ ɧɚɩɪɹɠɟɧɢɣ ɩɨ ɩɨɩɟɪɟɱɧɨɦɭ ɫɟɱɟɧɢɸ (ɪɢɫ. 2.1, ɜ). ɉɨɷɬɨɦɭ

A

ȿɫɥɢ ɢɡɜɟɫɬɧɵ ɜɧɭɬɪɟɧɧɟɟ ɭɫɢɥɢɟ N ɢ ɩɥɨɳɚɞɶ ɩɨɩɟɪɟɱɧɨɝɨ ɫɟɱɟɧɢɹ Ⱥ, ɬɨ ɩɨ (2.2) ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɧɚɩɪɹɠɟɧɢɹ σ ɜ ɥɸɛɨɦ ɫɟɱɟɧɢɢ ɢ ɩɨɫɬɪɨɢɬɶ ɷɩɸɪɭ σ . ɇɚ ɪɢɫ. 2.2, ɞ ɩɪɢɜɟɞɟɧɚ ɷɩɸɪɚ σ ɞɥɹ ɪɚɫɫɦɨɬɪɟɧɧɨɝɨ ɜɵɲɟ ɩɪɢɦɟɪɚ 1.

2.1.3. ɉɟɪɟɦɟɳɟɧɢɹ ɢ ɞɟɮɨɪɦɚɰɢɢ. Ɂɚɤɨɧ Ƚɭɤɚ

ɉɪɢ ɞɟɣɫɬɜɢɢ ɩɪɨɞɨɥɶɧɨɣ ɫɢɥɵ ɭɞɥɢɧɟɧɢɟ ɨɛɪɚɡɰɚ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɡɚɤɨɧɭ Ƚɭɤɚ (ɪɢɫ. 2.3)

Ɇɨɞɭɥɶ ɘɧɝɚ – ɮɢɡɢɱɟɫɤɚɹ ɤɨɧɫɬɚɧɬɚ ɦɚɬɟɪɢɚɥɚ. Ⱦɥɹ ɫɬɚɥɢ ȿ = (2 – 2,13)Â105 Ɇɉɚ. Ⱦɥɹ ɞɪɭɝɢɯ ɦɚɬɟɪɢɚɥɨɜ ȿ ɦɨɠɧɨ ɜɡɹɬɶ ɢɡ ɬɚɛɥɢɰ.

ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɨɩɪɟɞɟɥɟɧɢɟɦ (1.6) ɨɬɧɨɫɢɬɟɥɶɧɭɸ ɥɢɧɟɣɧɭɸ ɞɟɮɨɪɦɚɰɢɸ ɩɪɢ ɪɚɫɬɹɠɟɧɢɢ ε ɡɚɩɢɲɟɦ ɜ ɜɢɞɟ:

ɹɜɥɹɟɬɫɹ ɩɨɫɬɨɹɧɧɨɣ ɜɟɥɢɱɢɧɨɣ. Ⱥɛɫɨɥɸɬɧɚɹ ɜɟɥɢɱɢɧɚ ɷɬɨɝɨ ɨɬɧɨɲɟɧɢɹ

11