
Метод конечных элементов
Смоляр В.А.
5 февраля 2010 г.
1
Содержание
1 |
Введение |
|
4 |
|
2 |
Составной нагруженный в узлах стержень |
5 |
||
|
2.1 |
Постановка задачи для составного стержня . . . . . . . . . . |
5 |
|
|
|
2.1.1 |
Типовой элемент . . . . . . . . . . . . . . . . . . . . . |
6 |
|
|
2.1.2 Переход к составному стержню . . . . . . . . . . . . . |
8 |
|
|
|
2.1.3 |
Построение матрицы жесткости системы . . . . . . . |
9 |
|
2.2 |
Построение системы линейных алгебраических уравнений . |
10 |
|
2.2.1Матричная форма . . . . . . . . . . . . . . . . . . . . 10
2.2.2Ленточные матрицы . . . . . . . . . . . . . . . . . . . 12
2.2.3Пример ленточной матрицы . . . . . . . . . . . . . . . 12
2.2.4Предостережение - плохая обусловленность . . . . . . 13
2.3Пример вычислительной программы . . . . . . . . . . . . . . 14
3 Однородный стержень с непрерывной нагрузкой |
14 |
3.1Континуальная задача . . . . . . . . . . . . . . . . . . . . . . 14
3.2Дискретизация с помощью пробных функций . . . . . . . . . 15
3.2.1 Переход к слабой форме . . . . . . . . . . . . . . . . 16
3.2.2Метод Галёркина . . . . . . . . . . . . . . . . . . . . . 17
3.3 Матричное уравнение . . . . . . . . . . . . . . . . . . . . . . 19
3.3.1Вычисление матрицы жёсткости . . . . . . . . . . . . 19
3.3.2Вычисление правой части . . . . . . . . . . . . . . . . 21
3.3.3Подводим итоги . . . . . . . . . . . . . . . . . . . . . . 22
3.4Пример вычислительной программы . . . . . . . . . . . . . . 22
4 Стационарная диффузия или теплопроводность в стержне |
|
с неизолированными торцами |
24 |
4.1Краевая задача с условиями общего вида . . . . . . . . . . . 24
4.2Получение слабой формы . . . . . . . . . . . . . . . . . . . . 24
4.3Вычисление матричных коэффициентов . . . . . . . . . . . . 25
4.3.1 |
Первая строка . . . . . . . . . . . . . . . . . . . . . . |
25 |
4.3.2 |
Последняя строка . . . . . . . . . . . . . . . . . . . . |
26 |
4.3.3 |
Остальные строки . . . . . . . . . . . . . . . . . . . . |
28 |
4.3.4Правая часть . . . . . . . . . . . . . . . . . . . . . . . 30
4.3.5Подводим итоги . . . . . . . . . . . . . . . . . . . . . . 31
4.4Пример вычислительной программы . . . . . . . . . . . . . . 31
5 Общий вывод |
31 |
6 Нестационарные уравнения в частных производных второго порядка 32
6.1 Нестационарное уравнение диффузии - теплопроводности . . 32
2
6.1.1Одномерная геометрия . . . . . . . . . . . . . . . . . . 32
6.2Диффузия быстрых электронов в многослойной пластине . . 33
6.2.1Постановка задачи . . . . . . . . . . . . . . . . . . . . 33
6.2.2Приведение к канонической форме . . . . . . . . . . . 35
6.2.3 |
Методы аппроксимации по времени . . . . . . . . . . |
36 |
6.3 Вычисление матричных коэффициентов . . . . . . . . . . . . |
37 |
|
6.3.1 |
Дискретизация и усреднение по интервалам времени |
37 |
6.3.2Матричное уравнение на заданном временном интервале 39
6.3.3 Аппроксимация эволюционного уравнения . . . . . . 39
3
1Введение
В науке и технике постоянно приходится иметь дело с проблемой расчета систем, имеющих сложную геометрическую конфигурацию и физическую структуру. Компьютеры позволяют выполнять такие расчеты при помощи приближенных численных методов. Метод конечных элементов (МКЭ) является одним из них. В последние десятилетия он занял ведущее положение
иполучил широкое применение.
Сматематической точки зрения метод представляет собой обобщение метода Галёркина. Исходная задача, заданная дифференциальным уравнением записанным для искомой функции u(x), представляется в эквивалентной интегральной формулировке, а затем ищется приближенное решение последней в виде u n1 ui'i - комбинации конечного числа заданных пробных функций 'i. При этом коэффициенты ui вычисляются уже не из дифференциального уравнения, а из системы n дискретных алгебраических уравнений, для решения которой можно применить находящиеся в свободном доступе решатели систем алгебраических уравнений.
В методе конечных элементов пробные функции кусочно полиномиальны. Именно этим выбором определяется успех метода. Каждая функция 'i равна нулю на большей части области и отлична от нуля только в окрестности одного узла. В этой окрестности 'i составлена из полиномов небольшой степени, и все вычисления становятся максимально простыми.
Суменьшением максимального размера элементов увеличивается число узлов и неизвестных узловых параметров. Вместе с этим повышается возможность более точно удовлетворить уравнениям задачи и тем самым приблизиться к искомому решению. В настоящее время уже изучены многие вопросы, касающиеся сходимости приближенного решения методом конечных элементов к точному. Для линейных задач, когда неизвестные функции и операции над ними входят во все соотношения задачи только в первой степени, метод конечных элементов получил достаточно полное математическое обоснование [1].
Первая работа, где рассматривалась схема типа метода конечных элементов, принадлежит математику Куранту [2]. Построение метода с использованием физических соображений и его название ¾метод конечных элементов¿ содержатся в статье, написанной инженерами [3]. Такое сочетание специальностей авторов характерно для работ по методу конечных элементов. В последующем было опубликовано много статей и книг, посвященных этому методу и его различным модификациям. Некоторое представление об этом можно получить из списка литературы, например в [4].
Популярное изложение метода конечных элементов имеется в статье [6], которой мы будем в основном следовать. Раздел 2, в котором излагаются основные идеи метода конечных элементов на примере дискретной задачи о нагруженном стержне, взят из этой работы. Мы доведём изложение метода
4
до числа на примере континуальной задачи для стержня - подробно опишем каждый шаг аналитических вычислений и приведём текст программы, реализующий её вычислительный алгоритм. В Приложении дан текст программы на С++, в котором решена задача об одномерном нагруженном стержне с тестовым примером.
Метод конечных элементов применяется в решателях уравнений в частных производных второго порядка в больших универсальных компьютерных пакетах программ, например, MATLAB, FEMLAB. Это проприетарные программы. В больших универсальных компьютерных пакетах программ со свободным доступом - SCILAB, OCTAVE - используются накопленные в течение десятилетий библиотеки научных математических программ со свободным доступом - GSL (Gnu Sientific Lybrary), например. В этих библиотеках и построенных на их основе универсальных математических пакетах имеются решатели систем обыкновенных дифференциальных уравнений, но пока нет программ - решателей уравнений в частных производных с граничными условиями. По этой причине в случае необходимости, приходится для задачи, приводящей к уравнению в частных производных, создавать свой решатель для неё. В данном учебном пособии на простых примерах мы рассмотрим сущность метода конечных элементов и шаг за шагом, переходя от простого к сложному, покажем как реализовать эту сущность в вычислительной программе.
Естественными инструментом для решения этих задач является свободное программное обеспечение - компилятор G++ с дебаггером GDB в среде LINUX. Приведённые в Приложении программы отвечают требованиям лицензии GPL - 3, они могут свободно копироваться, распространяться и изменяться с любыми, в том числе и с коммерческими целями, хотя главная задача авторов - это применение в учебном процессе для обучения студентов технических и физических специальностей практическому применению метода конечных элементов.
2Составной нагруженный в узлах стержень
2.1Постановка задачи для составного стержня
Обратимся к дискретной задаче, состояние которой точно определяется конечным числом параметров. Рассмотрим упругий стержень в виде прямого кругового цилиндра, длина которого значительно больше его диаметра. Это позволяет отождествить стержень с его осью. Пусть несколько таких стержней расположены на оси x и соединены между собой (рисунок 1, (а)). Точки a и b закреплены, что условно изображено на рисунке. К осям стержней вдоль оси x приложим внешнюю нагрузку в узловых точках соединения стержней.
5
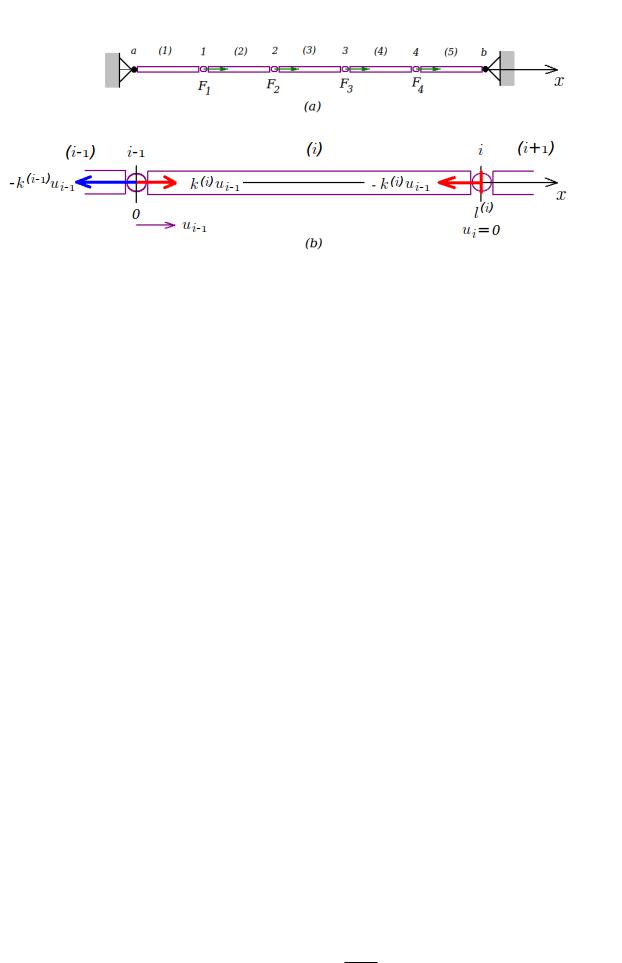
Рис. 1: Пример дискретной задачи
Очевидно, точки на осях стержней перемещаются вдоль x. Силы и перемещения считаются положительными, если они направлены в положительном направлении x. Задача состоит в определении перемещений точек, принадлежащих осям стержней и продольных внутренних сил в поперечных сечениях стержней.
Согласно методу конечных элементов, представим стержневую систему в виде элементов, соединенных в узлах. В качестве элементов примем отдельные стержни, а узлов - точки их соединения. На рисунке 1 в скобках указаны номера элементов, а без скобок - номера узлов.
2.1.1Типовой элемент
Условие равновесия Обратимся к типовому для данной системы элементу (i). На элемент с узлами i 1; i (рисунок 1, (b)) может действовать распределенная нагрузка интенсивности q(i)(x). Размерность интенсивности нагрузки - сила/(единица длины). Обозначим перемещения узлов элемента u(ii)1; u(ii). Обозначим длину элемента l(i). Получим задачу для функции перемещений точек оси x. Бесконечно малая часть элемента находится в равновесии под действием нагрузки и продольных внутренних упругих сил f(i)(x)
f(i) = c(i) |
du(i) |
; |
(1) |
|
dx |
||||
|
|
|
где c(i) > 0 носит название продольной жесткости стержня и определяется из опыта. Стержень будет находится в равновесии при равенстве упругих внутренних и приложенных внешних сил в каждом его элементе dx
|
df(i) |
|
df(i) + q(i)dx = 0; |
dx = q(i); |
(2) |
6

Пусть c(i) = const для элемента i. Подставляя (1) в (2) получим задачу относительно u(i)(x) в виде дифференциального уравнения и граничных условий
c(i) |
d2u(i) |
|
d2x = q(i); |
(3) |
u(i)(xi 1) = ui 1; u(i)(xi) = ui:
В нашем примере для случая дискретной задачи положим q(i) = 0 и будем считать, что на стержневую систему действуют только внешние силы сосредоточенные в узлах Fi. Внешняя нагрузка уравновешивается силами упругости стержней fi = Fi, и система находится в равновесии, получив в каждом узле некоторое смещение ui. Тогда решение уравнения (3) примет вид
|
(i) |
|
ui(i) ui(i)1 |
(i) |
|
(4) |
u |
|
(x) = |
l(i) |
x ui |
; |
На основании (4) можно заключить, что состояние типового элемента i, то есть u(i)(x); f(i)(x), точно определяется двумя параметрами - перемещениями его узлов u(ii); u(ji). Действительно, подставив решение (4), в (1), получим
fi(i) |
= (i) ui(i) |
ui(i)1 |
|
c(i) |
|
||
; (i) = |
|
: |
(5) |
||||
l(i) |
|||||||
Это делает задачу нахождения связи между перемещениями узлов составного стрежня и силами в узлах линейной.
Внутренние силы Рассмотрим внутренние упругие силы fi(i) действующие в узле i на элемент (i). Поскольку имеет место линейная задача, то они линейно зависят от u(ii)1; u(ii):
fi(i) = fii(i)ui(i) + fi;i(i) 1ui(i)1; |
(6) |
fi(i)1 = fi(i)1;iui(i) + fi(i)1;i 1ui(i)1: |
|
Здесь flt(i); l = i; i 1; t = i; i 1 есть внутренняя сила, действующая на элемент i в узле l и возникающая от единичного перемещения узла t. При этом перемещение другого узла равно нулю.
Воспользовавшись уравнением (5), получим
(i) |
|
(i) |
|
(i) |
|
(i) |
|
(i) |
|
(7) |
|||
fi |
= |
|
|
ui |
|
|
ui 1 |
; |
|||||
(i) |
= |
|
(i) |
(i) |
+ |
(i) |
(i) |
|
: |
||||
fi 1 |
|
|
ui |
|
|
|
ui 1 |
||||||
7
Матрица жесткости элемента Соотношения (5) можно представить в матричной форме. Введем столбцы f(i), u(i) и матрицу K(i)
|
f |
(i) |
|
|
u(i) |
|
|
|
(i) |
||
f(i) = |
|
fi(i) |
|
; u(i) = |
|
ui(i) |
|
; K(i) = |
(i) |
||
|
|
i 1 |
|
i 1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда (5) можно записать в виде
f(i) = K(i)u(i):
(i)
(i) :
(8)
(9)
Для упругой пружины коэффициент пропорциональности между силой и перемещением называется коэффициентом жесткости пружины. Аналогично K(i) носит название матрицы жесткости элемента r.
2.1.2Переход к составному стержню
От типового элемента перейдем к отдельным элементам данной системы. Для элементов с номерами 1 < i < n 1 справедливы все зависимости (4) - (9). Поскольку точки a; b неподвижны, то состояние элемента 1 определяется перемещением узла 1, а элемента n - перемещением узла n 1. На основании (4) будем иметь для элементов 1 и n соотношения
|
|
|
|
(1) |
|
u1(1) |
(1) |
|
|
|
(1) |
|
(1) |
|
|
|
|
||
|
|
|
u |
|
|
= |
|
x; f |
|
= |
|
u |
|
; |
|
|
|
||
|
|
|
|
l(1) |
|
|
|
|
(10) |
||||||||||
|
|
un(n)1 |
|
|
|
|
(n) |
|
|
|
|
|
|
|
(n) |
||||
|
(n) |
|
|
|
|
|
|
(n) |
|
|
|
(n) |
|
||||||
u |
|
= |
|
|
(x xn 1) + un 1 |
; f |
|
= |
|
un 1 |
: |
||||||||
|
l(n) |
|
|
|
|||||||||||||||
Зависимости (5) для элементов 1 и n примут соответственно вид:
f |
(1) |
= f |
(1)u(1) |
; |
f |
(n) |
= f |
(n) |
u(n) |
: |
(11) |
|
1 |
|
11 1 |
|
|
n 1 |
|
n 1;n 1 |
n 1 |
|
|
Сравнивая (5) или (9) для элемента 1 < i < n 1 с (11) для элементов 1 и n, можно заключить, что матрицы жесткости для жесткости для одноузловых элементов 1 и n имеют вид
(1) K(1) =
0
0
;
0
|
|
|
|
|
K(n) = |
0 |
0 |
: |
(12) |
0 |
(n) |
|||
|
|
|
|
|
|
|
|
|
|
Теперь все известно о каждом отдельном элементе системы. Следующим шагом является соединение элементов в узлах на основе условий:
uii = ui(i+1) = ui: |
(13) |
Отсюда следует, что состояние соединенных элементов или системы в целом определяется двумя узловыми перемещениями и рассматриваемая задача является дискретной.
8
Для всей системы можно записать соотношения типа (9) относительно суммарных для смежных элементов внутренних сил в узлах. Обозначим их fi. Введем столбцы f, u и матрицу жесткости всей системы K по формулам:
f = |
|
f...1 |
|
; u = |
u...1 |
|
; K = |
|
f11 |
|
f1;n 1 |
|
|
: |
|
|
|
|
|
|
|
|
|
fn 1;1 |
|
fn |
1;n |
1 |
|
|
|
|
fn 1 |
|
|
un |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь flt(l = 1; 2; t = 1; 2) есть суммарная внутренняя сила в узле l, возникающая от единичного перемещения узла l при нулевом перемещении узла t. Эти суммарные силы определяются через узловые силы в смежных элементах.
Mатричное соотношение типа (9) для всей системы будет:
f = Ku:
Учтём, что внутренние упругие силы fi уравновешивают приложенные в узлах внешние силы нагрузки Fi - они равны им по величине и противоположны по направлению. Тогда матричное соотношение для системы будет иметь вид
F = Ku: |
(14) |
2.1.3Построение матрицы жесткости системы
Из (13) следует,что матрица жесткости системы строится на основе коэффициентов жесткости для отдельных элементов. Алгоритмически выполнить это можно по-разному [5]. Например, можно для всех элементов строить матрицы жесткости одинаковой размерности равной размерности матрицы K, основываясь на столбце u перемещений всех узлов системы. Это возможно, поскольку flt(i) = 0, если по крайней мере один из узлов l или t не принадлежит элементу i. Из условия равновесия элемента i следует
flt(i) = f(i) при u(li) = 0; u(ti) = 1;
где f(i) > 0 при растяжении и f(i) < 0 при сжатии. В результате на основании (4), (5) и (10) получим
K(1) = |
|
0 |
: : : : : : |
; |
K(n 1) = |
: : : : : : |
|
|
f11 |
0 : : : : : : |
|
|
: : : : : : |
|
: : : |
: : : : : : |
|
|
: : : 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: : :
0;
fn 1;n 1
K(i 1) = |
0 : : : |
fii |
fi;i+1 |
0 |
: : : |
; |
|
0 : : : |
: : : |
: : : |
: : : : : : |
|
|
|
0 : : : fi+1;i |
fi+1;i+1 |
0 |
: : : |
|
|
|
|
|
|
|
|
|
|
0 : : : |
: : : |
: : : |
: : : : : : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
K = K(1) + : : : + K(i 1) + : : : + K(n 1):
Матрица K примет вид
|
|
(1) |
(2) |
(2) |
|
|
0 |
|
|
: : : |
|
|
|
: : : |
|
|
|
||||||
|
(2) |
|
|
(2) |
(3) |
|
(3) |
|
|
0 |
|
|
|
: : : |
|
|
|
||||||
|
|
0 |
|
(3) |
|
|
(2) (3) |
|
(4) |
|
|
|
|
0 |
|
|
|
|
|||||
K = |
|
: : : |
|
|
: : : |
|
|
: : : |
|
: : : |
|
|
|
: : : |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: : : |
|
|
0 |
|
|
(n |
|
2) |
|
(n 2) |
(n |
|
1) |
(n |
|
|
1) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: : : |
|
|
: : : |
|
|
0 |
|
(n 1) |
|
|
(n |
|
1) |
|
|
|
(n) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(15) |
||
Подставляя |
сюда вместо F его выражение согласно (2.1.2), окончатель- |
||||||||||||||||||||||
но получим систему алгебраических уравнений относительно смещений элементов в узлах ui
8 |
( (1) + (2):):u: |
1 (2)u2 |
=: :F:1; |
(16) |
> |
(i 1)ui 1 + ( (i 1) + (i))ui + (i+1)ui+1 |
= Fi; |
||
> |
|
|
|
|
> |
: : : |
|
: : : |
|
> |
|
|
||
< |
|
|
|
|
> |
(n 1)u1 + ( (n 1) + (n))u2 |
= Fn; |
|
|
>
>
>
:
В результате решения системы уравнений (16) находятся u(i), во всех элементах системы.
Таким образом, схема метода конечных элементов для дискретных задач состоит из представления системы в виде совокупности отдельных элементов, использования точного решения для типового элемента и соединения элементов в систему. Матрица жесткости всей системы определяется посредством матриц жесткости отдельных элементов и является матрицей системы алгебраических уравнений относительно неизвестных узловых перемещений.
:
2.2Построение системы линейных алгебраических уравнений
2.2.1Матричная форма
Метод конечных элементов сводит решение линейной задачи к решению системы линейных алгебраических уравнений
f11u1 + f12u2 + : : : + f1nun = F1; |
(17) |
: : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : |
|
fn1u1 + fn2u2 + : : : + fnnun = Fn: |
|
Здесь ui (i = 1; 2; : : : ; n) - неизвестные, Fi (i = 1; 2; : : : ; n) - заданные свободные члены, fij (i; j = 1; 2; : : : ; n) – коэффициенты при неизвестных.
10
