
Аналоговая электроника
.pdf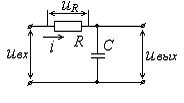
ни цепи увеличивать, то напряжение uR будет приближаться к значению
Um , а напряжение uC – к нулевому значению. В этом случае RC–цепь диф-
ференцирующей уже не является.
При очень большой величине tИ прямоугольный импульс
пройдет через RC-цепь почти без искажений, так как за время импульса
напряжение на конденсаторе не успевает измениться, и импульс на рези-
сторе R практически повторяет по форме импульс на входе. В этом случае
RC-цепь дифференцирующей также не является, а называется переходной
(разделительной).
Дифференцирующие цепи чаще всего применяются в импульсных схемах для формирования кратковременных импульсов напряжения из бо-
лее длительных импульсов, имеющих крутой фронт или срез. Они также используются для выполнения математической операции дифференциро-
вания.
1.1.3. Интегрирующая RC-цепь
Интегрирующей называется линейная цепь, выходной сигнал кото-
рой uВЫХ t связан с входным сигналом uВХ t соотношением:
t |
|
uВЫХ t k uВХ t dt u 0 , где k const . |
(13) |
0 |
|
Для интегрирования импульсов часто применяется простейшая ин-
тегрирующая RC-цепь (ИЦ), схема которой приведена на рис. 6.
Рис. 6. Интегрирующая RC-цепь
11
Такая цепь не может выполнить точно преобразование (13). Дейст-
вительно, согласно схеме:
|
1 |
t |
1 |
t |
1 |
t |
|
|
uВЫХ t |
i t dt |
uВХ t dt |
uВЫХ t dt . |
(14) |
||||
C |
RC |
RC |
||||||
|
|
0 |
|
0 |
|
0 |
|
Из (14) видно, что первое слагаемое есть результат точного интегри-
рования, а второе слагаемое имеет смысл погрешности. Эта погрешность будет незначительной, если выполняется условие tИ. Тогда можно за-
писать:
|
1 |
t |
|
|
uВЫХ t |
uВХ t dt . |
(15) |
||
RC |
||||
|
|
0 |
|
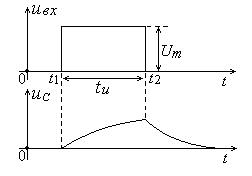
Если входной сигнал ИЦ представляет собой прямоугольный им-
пульс, то в момент времени t1 (рис. 7) начинается медленный экспоненци-
альный заряд конденсатора C , который продолжается все время действия импульса tИ . В момент окончания импульса t2 начинается медленный экспоненциальный разряд конденсатора, продолжающийся после оконча-
ния входного импульса. При выполнении неравенства tИ этот процесс приближенно представляет собой линейно нарастающее напряжение, что и должно происходить при интегрировании сигнала, представляющего собой
Рис. 7. Диаграммы напряжений на элементах интегрирующей RC-цепи
константу (во временном интервале t1–t2, рис. 7). Таким образом, RC–цепь,
приведенная на рис. 6, в данном случае является интегрирующей.
12
1.1.4. Фильтрующие свойства RC-цепей
При воздействии синусоидальных (гармонических) колебаний на це-
пи, конфигурация которых приведена на рис. 3, рис. 6, их комплексный ко-
эффициент передачи в общем случае будет определяться выражением:
|
|
|
|
|
K |
jw |
UВЫХ |
. |
(16) |
|
||||
|
|
UВХ |
|
|
Для линейных цепей K jw зависит от частоты входного напряжения
и элементов, входящих в цепь. В соответствии с формулой Эйлера можно записать:
K jw K w ej w . |
(17) |
|||
Здесь величина K w |
|
K jw |
|
представляет собой амплитудно- |
|
|
|||
частотную характеристику (АЧХ) цепи, а w argK jw – фазо–частотную характеристику (ФЧХ) цепи. В соответствии с вышесказанным, для RC-
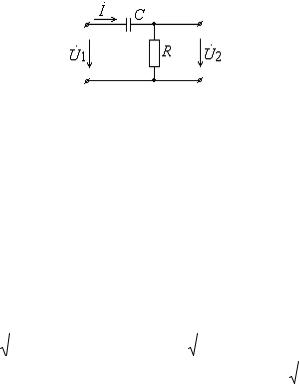
цепи, приведенной на рис. 8 (RC-цепь, аналогичная приведенной на рис. 3), получим выражения:
Рис. 8. RC–цепь, обладающая свойствами фильтра высоких частот
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
wC |
2 |
|
|
|
1 |
|
||||||
|
|
|
|
UВЫХ |
|
|
|
|
I ZR |
|
|
|
|
|
R |
|
|
|
R R |
j |
|
|
|
|
|
|
|
|
|
R R j |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wC |
|
|
|
|
|
|
|
wC |
|
|||||||||||||||||
K |
jw |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
UВХ |
I ZR ZC |
R |
j |
1 |
|
|
R |
2 |
|
|
1 |
|
|
|
|
|
|
|
1 wCR 2 |
|
|
||||||||||||||||||||||||||
|
|
wCR 2 |
|
|
|
|
|
|
|
|
|
|
|
|
wC |
|
|
|
|
wC 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
j |
|
|
wCR |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 wCR 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 wCR 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
K w |
|
K jw |
|
|
|
|
|
|
wCR 4 wCR 2 |
|
|
RwC |
wCR 2 |
1 |
|
|
|
|
wCR |
|
|
. (18) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 wCR 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 wCR 2 |
|
|
|
|
|
|
|
|
|
wCR 2 1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
13
|
|
wCR |
|
wCR 2 |
|
|
1 |
|
|
argK |
jw w arctg |
|
|
|
|
arctg |
|
. |
(19) |
2 |
2 |
|
|||||||
|
|
|
wCR |
|
|||||
|
|
1 wCR |
1 wCR |
|
|
||||
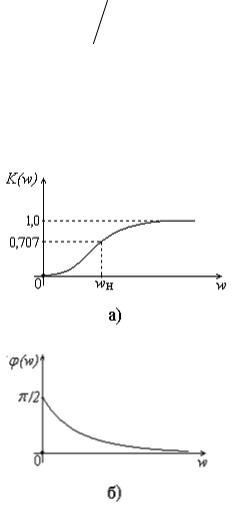
Выражение (18) представляет собой АЧХ цепи (рис. 8), выражение
(19) представляет собой ФЧХ данной цепи. На рис. 9а, б показаны графики АЧХ и ФЧХ, построенные в соответствии с выражениями (18) и (19).
Рис. 9. Амплитудно – частотная (а) и фазо – частотная (б)
характеристики RC-цепи, приведенной на рис. 8
Из графика АЧХ (рис. 9а) видно, что RC-цепь, приведенная на рис. 8,
для сигналов разных частот имеет разный коэффициент их передачи на выход. В области низких частот имеет место сильное подавление сигналов
(для постоянной составляющей К(0) = 0). Наоборот, для сигналов, имею-
щих высокие частоты, коэффициент передачи близок к единице. Такая цепь обладает частотно – избирательными свойствами и называется фильтром высоких частот (ФВЧ), поскольку на выход этой цепи пропус-
каются только сигналы с частотами выше некоторой частоты н. Эта час-
тота называется нижней граничной частотой полосы пропускания фильтра.
14
Считается, что частоты ниже н на выход ФВЧ не пропускаются. Частота
н соответствует уменьшению коэффициента передачи К( ) на величину
1/20,5 = 0,707 и является границей раздела между верхними и нижними час-
тотами для данного фильтра. Связь между н и постоянной времени дан-
ной цепи = RC определяется соотношением н=1/ .
Для RC-цепи, приведенной на рис. 10, также можно получить соот-
ветствующее выражение для комплексного коэффициента передачи:
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
K jw |
UВЫХ |
|
I ZС |
|
|
jwC |
|
1 |
|
|
1 RjwC |
|
1 |
|
RwC |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
. |
|||
UВХ |
I ZR ZC |
R |
1 |
RjwC 1 |
|
1 wCR 2 |
1 wCR 2 |
1 wCR 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
jwC
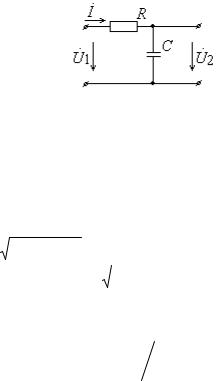
Рис. 10. RC–цепь, обладающая свойствами фильтра низких частот
Тогда выражение для ее АЧХ будет иметь вид:
K w |
|
K jw |
|
|
1 wCR 2 |
|
|
1 |
|
(20) |
|
|
|
||||||||
|
|
1 wCR 2 |
|
|
|
|||||
|
|
wCR 2 1 |
||||||||
|
|
|
|
|
|
|
|
Соответственно, выражение для ее ФЧХ будет иметь вид:
|
|
|
wCR |
|
|
1 |
|
|
|
argK |
jw w arctg |
|
|
|
arctg wCR |
(21) |
|||
|
2 |
2 |
|||||||
|
|
|
1 wCR |
|
|
|
|||
|
|
|
|
1 wCR |
|
|
|
||
На рис. 11а и рис. 11б показаны графики АЧХ и ФЧХ данной цепи,
построенные в соответствии с выражениями (20) и (21).
Из графика АЧХ (рис. 11а) видно, что RC-цепь, приведенная на рис. 9, также обладает частотно – избирательными свойствами. В данном слу-
чае на ее выход будут проходить практически беспрепятственно, сигналы,
15
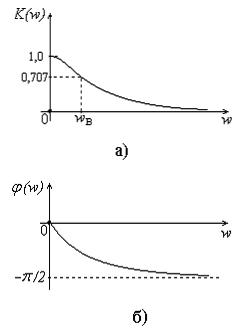
Рис. 11. Амплитудно – частотная (а) и фазо – частотная (б) характеристики RC-цепи, приведенной на рис. 10
имеющие низкие частоты (до частоты в). Сигналы с более высокими час-
тотами будут сильно подавляться. То есть, в данном случае на выход цепи будут пропускаться только сигналы с низкими частотами (включая посто-
янную составляющую). Подобные цепи называются фильтрами низких частот (ФНЧ). Частота в называется верхней граничной частотой полосы пропускания ФНЧ. Связь между в и постоянной времени для данной цепи
такая же, как для предыдущей цепи.
1.2. Лабораторная работа № 1
Дифференцирующие и интегрирующие RC-цепи
Цель работы: Изучение свойств и принципа работы простейших
пассивных дифференцирующей и интегрирующей RC-цепей.
16
Выполнение лабораторной работы
Подготовка к работе.
1.Изучить теоретическую часть пособия для данной лабораторной
работы.
2.Рассчитать значения постоянных времени дифференцирующей
(τдиф) и интегрирующей (τинт) цепей для своего варианта работы, в соответ-
ствии с приведенной ниже таблицей.
Внимание! Выбор варианта работы осуществляется преподавателем.
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
Rдиф, кОм |
1 |
0,68 |
0,47 |
1 |
0,68 |
0,47 |
Cдиф, мкФ |
0,01 |
0,01 |
0,01 |
0,01 |
0,01 |
0,01 |
Rинт, кОм |
10 |
10 |
10 |
10 |
10 |
10 |
Cинт, мкФ |
0,1 |
0,22 |
0,33 |
0,1 |
0,22 |
0,33 |
3. Построить предполагаемые временные диаграммы, аналогичные рис. 4, рис. 7, полагая τдиф ≤ 10 Ти и τинт ≥ 10 Ти, для случая, когда длитель-
ность импульса на входе обеих цепей Ти одинакова.
Практическое выполнение работы.
1. Собрать дифференцирующую цепь (рис. 3), используя элементы,
соответствующие номеру вашего варианта.
2. Подключить на вход собранной ДЦ генератор импульсов прямо-
угольной формы (имеется в составе стенда). На выход цепи подключить осциллограф. Для частоты входных импульсов f = 5 кГц (при этом Ти = 100
мкс) зарисовать на одном графике осциллограммы входного и выходного сигналов, сравнить с результатами предварительной подготовки.
3. По полученной диаграмме выходного сигнала определить оценоч-
ное значение τдиф, сравнить его с расчетным значением.
17
4. Собрать интегрирующую цепь (рис. 6), используя элементы, соот-
ветствующие номеру вашего варианта и выполнить для нее п. 2.
5. По полученной диаграмме выходного сигнала определить оценоч-
ное значение τинт, сравнить его с расчетным значением.
6. Сделать выводы по проделанной работе и полученным результа-
там.
Контрольные вопросы и задания
1. Дайте определение дифференцирующей цепи, изобразите ее схе-
му.
2. Запишите условие, при котором цепь является дифференцирую-
щей.
3. Изобразите на графике ожидаемый сигнал на выходе ДЦ при им-
пульсном воздействии на ее входе.
4. Изобразите отклик на выходе ДЦ при воздействии на ее входе дру-
гих характерных сигналов (гармонического, линейно нарастающего и др.)
5.Дайте определение интегрирующей цепи, изобразите ее схему.
6.Запишите условие, при котором цепь является интегрирующей.
7.Изобразите на графике ожидаемый сигнал на выходе ИЦ при им-
пульсном воздействии на ее входе.
8. Изобразите отклик на выходе ИЦ при воздействии на ее входе других характерных сигналов (гармонического, линейно нарастающего и т.д.)
1.3. Лабораторная работа № 2
Фильтрующие свойства RC-цепей
18
Цель работы: Изучение частотно – избирательных (фильтрующих)
свойств простейших RC-цепей, фильтры высоких и низких частот.
Выполнение лабораторной работы
Подготовка к работе.
1.Изучить теоретическую часть пособия для данной лабораторной
работы.
2.Рассчитать значение постоянной времени для своего варианта работы в соответствии с приведенной ниже таблицей. По нему определить значение fн для ФВЧ и fв для ФНЧ (они в данном случае будут одинаковы-
ми).
Внимание! Выбор варианта работы осуществляется преподавателем.
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
|
R |
кОм |
1 |
2,2 |
0,47 |
3,3 |
0,68 |
4,7 |
C |
мкФ |
0,1 |
0,01 |
0,1 |
0,01 |
0,1 |
0,01 |
3. Используя формулы (3) – (6), рассчитать и построить на отдельных листах бумаги графики АЧХ и ФЧХ соответствующих RC-цепей для сво-
его варианта работы.
Практическое выполнение работы.
1. Собрать RC-цепь, приведенную на рис. 8. Подключить к входу це-
пи генератор синусоидальных сигналов (имеется в составе стенда). На вы-
ход цепи подключить осциллограф (или цифровой вольтметр). Снять зави-
симость амплитуды выходного сигнала от частоты сигнала на входе. По-
строить экспериментально полученную зависимость АЧХ на одном графи-
ке с рассчитанной, сравнить их. Результаты сравнения отразить в выводах.
19
2. По экспериментально полученной АЧХ определить значение fн,
сравнить его значение с расчетным. Результаты сравнения отразить в вы-
водах.
3. Собрать RC-цепь, приведенную на рис. 9. Экспериментально снять для нее АЧХ, построить ее на одном графике с расчетной, определить зна-
чение fв, проделать все аналогично п.п. 1, 2. Сравнить экспериментально полученные характеристики с расчетными, результаты сравнения отразить
ввыводах.
4.Сделать выводы по проделанной работе и полученным результа-
там.
Контрольные вопросы и задания
1.Дайте определение фильтра высоких частот, изобразите схему рассматриваемого ФВЧ.
2.Изобразите и объясните АЧХ и ФЧХ для ФВЧ.
3.Дайте определение фильтра низких частот, изобразите схему рас-
сматриваемого ФНЧ.
4.Изобразите и объясните АЧХ и ФЧХ для ФНЧ.
5.Что такое граничные частоты ФВЧ и ФНЧ, как определяются их полосы пропускания?
6.Какие еще разновидности фильтров можете назвать? Поясните их особенности с помощью их АЧХ.
1.4.Рекомендуемая литература
1.Попов В.П. Основы теории цепей. М.: Высш. шк., 2005.
2.Бессонов Л.А. Теоретические основы электротехники. М.: Высш.
шк., 1996.
20
