
view
.pdfний подготовки 653300 (190600.65), 653400 (190700.65) и направлению подготовки бакалавров 552100 (190500.62) и в дальнейшем выпустить сборник профессионально ориентированных практических задач для самостоятельной проработки по некоторым разделам теории вероятностей, математической статистики и регрессионного анализа с образцами их решения, направленными на оказание помощи студентам в освоении методических основ применения тех или иных стандартных положений раздела.
131
СПИСОК ЛИТЕРАТУРЫ
Основные литературные источники, рекомендуемые для самостоятельной углубленной проработки материала
1.Вдовин, А. Ю. Индивидуальные задания по теории вероятностей и математической статистике : учебное пособие / А. Ю. Вдовин, С. Н. Удинцева. – Екатеринбург : Изд. Урал. гос. лесотехн. ун-та, 2009.
2.Ганченко, О. И. Статистика автомобильного транспорта : учебник/ О. И. Ганченко, И. М. Алексеева. – М.: «Экзамен», 2005.
3.Гусак, А. А. Теория вероятностей. Спровочное пособие к решению задач /
А.А. Гусак, Е. А. Бричикова. – МН.: ТетраСистемс, 2002.
4.Медведько, М. А. Сборник задач по теории вероятностей : учебное пособие / М. А. Медведько, Л. Ю. Шипик. – Зерноград : Изд. ФГОУ ВПО «АЧГАА», 2005.
5.Степунина, О. А. Основы теории случайных процессов : учебно-практическое пособие / О. А.Степунина, Е. Б. Трофимова. – Бузулук : Изд. БГТИ (филиала) ГОУ ОГУ, 2006.
6.Феофанова, Л. Н. Теория вероятностей. Стандартные задачи с основными положениями теории : учебное пособие / Л. Н. Феофанова., А. Е. Годенко, В. Н. Стяжин, Л. А. Исаева. – Волгоград : Изд. ВолгГТУ, 2009.
Дополнительные литературные источники
7.Вентцель, Е. С. Теория вероятностей. / Е. С. Вентцель. – М. : Физматгиз, 1963.
8.Гмурман, В. Е. Введение в теорию вероятностей и математическую статистику /
В.Е. Гмурман. – М. : Высшая школа, 1977.
9.Гурский, В. И. Сборник задач по теории вероятностей и математической статистике / В. И. Гурский. – МН. : Высшая школа, 1984.
10.Колмагоров, А. Н. Основные понятия теории вероятностей / А. Н. Колмагоров.
– М. : Наука, 1974.
11.Копылов, Г. Н. Задачник по теории вероятностей / Г. Н. Копылов, Н. Н. Суханова. – Волгоград : ВолГУ, 1997.
12.Космачева, И. М. Задачи теории вероятностей и математической статистики / И. М. Космачева. – Астрахань : Гостехуниверситет, 2002.
13.Макарова, Е. Л. Задачник-практикум по теории вероятностей / Е. Л. Макарова.
– Волгоград : Перемена, 2002.
14.Студенецкая, В. Н. Решение задач по статистике, комбинаторике и теории вероятностей / В. Н. Студенецкая. – Волгоград : Учитель, 2005.
15.Чистяков, В. П. Курс теории вероятностей / В. П. Чистяков.. – М. : Наука, 1987.
132
Приложения
133

Приложение А
Ключи ответов к текстам для подготовки к экзаменам
Номер |
|
|
|
|
Номер варианта |
|
|
|
|
||
задачи |
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
1 |
3 |
3 |
3 |
2 |
3 |
1 |
|
3 |
1 |
4 |
1 |
2 |
1 |
1 |
1 |
3 |
1 |
3 |
|
2 |
2 |
4 |
1 |
3 |
1 |
2 |
1 |
4 |
1 |
1 |
|
2 |
2 |
3 |
3 |
4 |
2 |
1 |
2 |
3 |
2 |
1 |
|
1 |
3 |
1 |
4 |
5 |
2 |
2 |
1 |
4 |
3 |
3 |
|
1 |
4 |
4 |
3 |
6 |
1 |
3 |
4 |
1 |
3 |
2 |
|
3 |
1 |
3 |
4 |
7 |
3 |
2 |
5 |
4 |
5 |
4 |
|
1 |
2 |
5 |
2 |
8 |
1 |
2 |
3 |
4 |
2 |
1 |
|
1 |
1 |
3 |
2 |
9 |
3 |
2 |
1 |
4 |
1 |
2 |
|
3 |
1 |
2 |
4 |
10 |
1 |
2 |
1 |
4 |
2 |
4 |
|
3 |
4 |
2 |
3 |
11 |
4 |
2 |
3 |
4 |
1 |
3 |
|
4 |
2 |
1 |
1 |
12 |
1 |
1 |
4 |
1 |
1 |
2 |
|
1 |
3 |
3 |
1 |
|
|
|
|
|
|
|
Приложение Б |
|
Справочные материалы для решения задач |
||||||
|
|
|
|
|
|
|
|
№№ |
Понятия, обозначения |
|
|
Содержание, формула |
|||
п/п |
|
|
|||||
|
|
|
|
|
|
|
|
|
Множество |
|
|
|
|||
1 |
Множество A – совокупность каких-либо объектов |
||||||
|
|
|
|
a , называемых элементами множества: a A |
|||
2 |
|
|
|
|
|
|
|
Дополнение A (не A) |
|
A содержит все элементы, не принадлежащие A |
|||||
|
|
||||||
3 |
Равенство множеств |
Два множества A и B равны между собой, если они |
|||||
|
A = B |
состоят из одних и тех же элементов |
|||||
4 |
Объединение (сумма) |
Множество C состоит из всех элементов, принадле- |
|||||
|
множеств C = A + B |
жащих или множеству A, или множеству B, или |
|||||
|
|
|
|
и A и Bодновременно |
|
||
5 |
Пересечение (произ- |
Множество C состоит из элементов, принадлежа- |
|||||
|
ведение) множеств |
щих одновременно и множеству A и множеству B |
|||||
|
C = A B |
|
|
|
|
||
6 |
Разность двух |
C состоит из элементов множества A, которые не |
|||||
|
множеств C = A − B |
являются элементами множества B |
|||||
7 |
Эквивалентные |
Два множества называются эквивалентными, если |
|||||
|
множества |
между ними установлено взаимно-однозначное соот- |
|||||
|
|
|
|
ветствие |
|
||
8 |
Счетные множества |
Бесконечные множества, эквивалентные множеству |
|||||
|
|
|
|
натуральных чисел N |
|
||
9 |
Перестановки. |
Соединения, отличающиеся только порядком эле- |
|||||
|
Число перестановок |
ментов, называются перестановками. Число переста- |
|||||
|
|
|
|
новок из n элементов Pn |
= n!, где |
||
|
|
|
|
n!=1 2 3 4 K n |
0!=1 |
||
134

|
|
|
|
|
|
|
|
|
|
|
|
Продолжение прил. Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
№№ |
Понятия, обозначения |
|
|
|
|
|
|
|
Содержание, формула |
|||
п/п |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
Размещения. |
Соединения из n различных элементов по m , отли- |
||||||||||
|
Число размещений |
чающихся друг от друга составом элементов либо их |
||||||||||
|
|
порядком, называются размещениями. Число разме- |
||||||||||
|
|
щений из n по m |
|
|
||||||||
|
|
Am = |
|
|
n! |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(n − m)! |
|
|
||||||||
|
|
n |
|
|
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
11 |
Сочетания. |
Соединения из n различных элементов по m , отли- |
||||||||||
|
Число сочетаний |
чающихся друг от друга хотя бы одним элементом, |
||||||||||
|
|
называются сочетаниями. |
||||||||||
|
|
Число сочетаний из n по m |
||||||||||
|
|
Cm = |
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
(n |
− m)!m! |
|
|
|||||||
|
|
n |
|
|
|
|||||||
|
|
Cm = Cn−m ; |
|
|
|
|
|
|||||
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
C0 |
=1;Cm+1 |
= Cm + Cm+1; |
||||||||
|
|
n |
|
|
|
n+1 |
|
n |
|
n |
||
|
|
Cn0 + Cn1 + Cn2 +K + Cnn−1 + Cnn = 2n. |
||||||||||
12 |
Стохастический |
Это опыт (испытание), результат которого заранее не |
||||||||||
|
эксперимент |
определен |
|
|
|
|
|
|||||
13 |
Достоверное событие |
Результат, который обязательно наступает при осу- |
||||||||||
|
|
ществлении данного комплекса условий (опыта, экс- |
||||||||||
|
|
перимента) называется достоверным событием |
||||||||||
14 |
Случайное событие |
Это событие, которое может произойти, а может и не |
||||||||||
|
|
произойти в данном испытании |
||||||||||
15 |
Невозможное событие |
Это событие, которое не может произойти при дан- |
||||||||||
|
|
ном комплексе условий |
||||||||||
16 |
Относительная |
Отношение ν (A) = |
m |
числа экспериментов m , за- |
||||||||
|
частота события A |
|||||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
вершившихся событием A, к общему числу n про- |
||||||||||
|
|
веденных экспериментов |
||||||||||
17 |
Статистическое опре- |
Если при неограниченном увеличении числа экспе- |
||||||||||
|
деление вероятности |
риментов относительная частота события ν(A) |
||||||||||
|
|
стремится к некоторому фиксированному числу, то |
||||||||||
|
|
событие A стохастически устойчиво и это число |
||||||||||
|
|
p(A) называют вероятностью события A |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
Определение вероят- |
P(A) = |
m |
, где m – число исходов стохастического |
||||||||
|
ности в классической |
|||||||||||
|
|
|||||||||||
|
схеме |
|
|
|
|
n |
|
|
|
|
|
|
|
эксперимента, благоприятствующих наступлению |
|||||||||||
|
|
|||||||||||
|
|
события A, n – общее число всех равновозможных |
||||||||||
|
|
исходов |
|
|
|
|
|
|
|
|||
135

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение прил. Б |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№№ |
Понятия, обозначения |
|
|
|
|
|
|
|
|
Содержание, формула |
|
|
|||||||||||
п/п |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
Вероятность суммы |
|
|
|
|
|
|
|
|
|
P(A+ B) = P(A) + P(B) − P(AB) |
||||||||||||
|
(объединения), двух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
событий A и B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
20 |
Вероятность произве- |
P(AB) = P(A) P(B/ A) = P(B) P(A| B) , |
|||||||||||||||||||||
|
дения двух зависимых |
где P(B | A) |
– условная вероятность события B при |
||||||||||||||||||||
|
событий A и B |
условии, что событие A с ненулевой вероятностью |
|||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
произошло |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
21 |
Независимые события |
Это такие события, для которых P(B | A) = P(B) |
|||||||||||||||||||||
|
A и B |
и P(A| B) = P(A). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Следовательно, P(AB) = P(A) P(B) |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
22 |
Схема Бернулли |
Стохастический эксперимент состоит из последова- |
|||||||||||||||||||||
|
|
тельности n независимых и одинаковых испытаний, |
|||||||||||||||||||||
|
|
в каждом из которых может произойти событие A |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
или событие, ему противоположное A с вероятно- |
|||||||||||||||||||||
|
|
стями соответственно равными p и q =1− p |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
23 |
Формула Бернулли |
Вероятность того, что в серии из n испытаний собы- |
|||||||||||||||||||||
|
|
тие A появится ровно m раз P (m) = Cm pm qn−m |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
Вероятность того, что при n испытаниях A появля- |
|||||||||||||||||||||
|
|
ется не менее m1 и не более m2 |
раз вычисляется по |
||||||||||||||||||||
|
|
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
||
|
|
Pn (m1 ≤ m ≤ m2 ) = ∑2 |
Cnm pm qn−m |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m=m1 |
|
|
|
|
|
|
|
|
|
||
24 |
Формула Пуассона |
При достаточно большом n и малом p (если |
|||||||||||||||||||||
|
|
a = np <10) |
P (m) ≈ |
am |
e−a |
(табл. П.В.1 прил. В) |
|||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
m! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
k |
a |
m |
|
|
|
|
|
|
|
|
|
|
|
|
Pn (m ≤ k) ≈ e−a ∑ |
|
|
(табл. П.В.2 прил. В) |
||||||||||||||||||
|
|
m! |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m=0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
25 |
Локальная формула |
При достаточно большом n |
|
|
|
|
|
|
|
||||||||||||||
|
Муавра-Лапласа |
и не слишком малых p и q |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
−x2 |
||||
|
|
P (m) ≈ |
|
|
|
ϕ(x), где ϕ(x) = |
|
|
e 2 и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
n |
|
npq |
|
|
|
|
|
|
|
2π |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
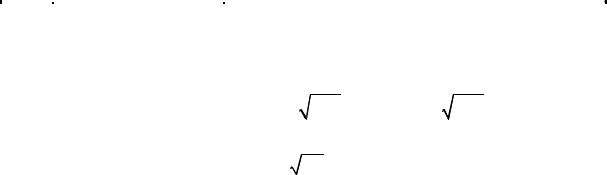
|
|
x = |
m |
− np |
|
; |
|
|
ϕ(−x) =ϕ(x) |
(табл. П.В.3 прил. В) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
136
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение прил. Б |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
№№ |
Понятия, обозначения |
|
|
|
|
|
|
Содержание, формула |
||||||||
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
Интегральная форму- |
Pn (m1 ≤ m ≤ m2 ) = Φ(x2 ) − Φ(x1) , |
||||||||||||||
|
ла Муавра-Лапласа |
|
|
m1 |
− np |
|
|
m2 |
− np |
|
||||||
|
|
где x = |
; |
x = |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
npq |
2 |
|
|
npq |
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
x −t2 |
|
|
|
|
||||||
|
|
Φ(x) = |
|
|
∫e 2 dt ; Φ(−x) = −Φ(x) |
|||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
2π |
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
(табл. П.В.3 прил. В) |
|
|
|
|
||||||||||
27 |
Понятие случайной |
Случайной величиной называют переменную вели- |
||||||||||||||
|
величины |
чину, которая принимает числовые значения в зави- |
||||||||||||||
|
|
симости от исходов испытания случайным образом |
||||||||||||||
28 |
Понятие дискретной |
ДСВ X – случайная величина, принимающая раз- |
||||||||||||||
|
случайной величины |
личные значения, которые можно записать в виде |
||||||||||||||
|
(ДСВ X ) |
конечной или бесконечной последовательности, то |
||||||||||||||
|
|
есть численные значения которой образуют конечное |
||||||||||||||
|
|
или счетное множество |
|
|
|
|
||||||||||
29 |
Закон распределения |
Соответствие между значениями x1,x2 ,... дискрет- |
||||||||||||||
|
дискретной случайной |
ной случайной величины и их вероятностями |
||||||||||||||
|
величины |
p1, p2 ,... называется законом распределения и мо- |
||||||||||||||
|
|
|||||||||||||||
|
|
жет быть задан таблично или аналитически (то есть с |
||||||||||||||
|
|
помощью формул). Если ДСВ X принимает конеч- |
||||||||||||||
|
|
ное множество значений x1,x2,...,xn соответст- |
||||||||||||||
|
|
венно с вероятностями p1, p2 ,..., pn , то ее закон рас- |
||||||||||||||
|
|
пределения определяется формулами |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
P(X = xk ) = pk , |
k =1,2,...,n |
|
и ∑ pk =1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
||
|
|
Если ДСВ X принимает бесконечную последова- |
||||||||||||||
|
|
тельность значений x1,x2,x3... |
соответственно с ве- |
|||||||||||||
|
|
роятностями |
|
p1, p2 , p3,...,, то ее закон распределе- |
||||||||||||
|
|
ния определяется формулами |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
||
|
|
P(X = xk ) = pk , |
k =1,2,...,n |
|
и ∑ pk =1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
||
30 |
Понятие непрерывной |
НСВ X – случайная величина, которая может при- |
||||||||||||||
|
случайной величины |
нимать любые значения из некоторого промежутка, |
||||||||||||||
|
(НСВ X ) |
то есть множество значений непрерывной случайной |
||||||||||||||
|
|
величины несчетно |
|
|
|
|
||||||||||
31 |
Функция распределе- |
Функцией распределения случайной величины X |
||||||||||||||
|
ния. Свойства функ- |
называется функция действительного переменно- |
||||||||||||||
|
ции распределения |
го x , определяемая равенством F(x) = P(X < x) , |
||||||||||||||
|
|
где P(X < x) – вероятность того, что случайная |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
137

Продолжение прил. Б
№№ |
Понятия, обозначения |
Содержание, формула |
|
п/п |
|
|
|
|
|
величина X принимает значение, меньше x . |
|
|
|
Функция распределения F(x) для ДСВ X , которая |
|
|
|
может принимать значения x1,x2 ,... xn |
c соответст- |
|
|
вующими вероятностями p1, p2 ,..., pn |
имеет вид |
|
|
F(x) = ∑P(X < xk ) , где символ xk |
< x означает, |
|
|
xk <x |
|
|
|
что суммируются вероятности pk тех значений, ко- |
|
|
|
торые меньше x . |
|
|
|
Функция является разрывной. |
|
|
|
Случайная величина X называется непрерывной, |
|
|
|
если ее функция распределения F(x) является не- |
|
|
|
прерывно дифференцируемой. Вероятность того, что |
|
|
|
СВХ примет значение из промежутка [α;β ), равна |
|
|
|
разности значений ее функции распределения на |
|
|
|
концах этого полуинтервала: |
|
|
|
P(α ≤ X < β) = F(β) − F(α) |
|
Свойства функции распределения
1.0 ≤ F(x) ≤1
2.Если x1 < x2 , то F(x1) ≤ F(x2 ) , то есть функция
распределения является неубывающей
3. Функция F(x) в точке x0 непрерывна слева, то
есть lim F(x) = F(x0 ) ; F(x0 − 0) = F(x0 )
x→x0 −0
4. Если все возможные значения СВХ принад-лежат интервалу (a;b), то F(x) = 0 при x ≤ a ,
F(x) =1 при x ≥ b
5. Если все возможные значения СВХ принадлежат бесконечному интервалу (−∞;+∞), то
lim F(x) = 0; lim F(x) =1;
x→−∞ x→+∞
Если X – непрерывная случайная величина, то вероятность того, что она примет одно заданное опре-
деленное значение, равна нулю: P(X =α) = 0
Отсюда следует, что для непрерывной случайной величины выполняются равенства:
P(α < X < β) = P(α ≤ X ≤ β) = P(α ≤ X < β) = = P(α < X ≤ β) = F(β) − F(α)
138

|
|
|
|
|
|
Продолжение прил. Б |
|
|
|
|
|
|
|||
№№ |
Понятия, обозначения |
|
Содержание, формула |
||||
п/п |
|
|
|
|
|
|
|
32 |
Плотность распреде- |
Плотностью распределения (дифференциальной |
|||||
|
ления вероятностей |
функцией распределения) вероятностей НСВ X в |
|||||
|
непрерывной случай- |
точке x называют предел отношения вероятности |
|||||
|
ной величины. |
попадания значений этой величины в интервал |
|||||
|
Свойства функции |
(x;x + x) к длине |
x этого интервала, когда по- |
||||
|
плотности распреде- |
||||||
|
ления |
следняя стремится к нулю: |
|
|
|||
|
|
P(x < X < x + |
x) |
|
|||
|
|
f (x) = lim |
Следовательно, |
||||
|
|
|
|
||||
|
|
x→0 |
|
x |
|
|
|
|
|
f (x) = F′(x) , то есть плотность распределения есть |
|||||
|
|
первая производная от функции распределения |
|||||
|
|
НСВХ. Вероятность того, что НСВХ примет значе- |
|||||
|
|
ние, принадлежащее интервалу (a;b), определяется |
|||||
|
|
|
|
|
b |
|
|
|
|
равенством P(a < X < b) = ∫ f (x)dx. |
|||||
|
|
|
|
|
a |
|
|
32 |
Плотность распреде- |
Зная плотность распределения, можно найти функ- |
|||||
|
ления вероятностей |
|
|
|
x |
|
|
|
непрерывной случай- |
цию распределения F(x) = ∫ |
f (x)dx. |
||||
|
ной величины. |
|
|
|
−∞ |
||
|
Свойства функции |
Свойства функции плотности |
|
|
|||
|
плотности распреде- |
1. Плотность распределения f (x) - неотрицательная |
|||||
|
ления |
функция, то есть |
f (x) ≥ 0. |
|
|
||
|
|
|
|
||||
|
|
2. Несобственный интеграл по бесконечному проме- |
|||||
|
|
жутку (−∞;+∞) от функции плотности вероятно- |
|||||
|
|
|
|
+∞ |
|
|
|
|
|
стей равен единице: ∫ |
f (x)dx =1. |
||||
|
|
|
|
−∞ |
|
|
|
|
|
3. Если все возможные значения случайной величи- |
|||||
|
|
|
|
|
|
|
β |
|
|
ны принадлежат отрезку [α;β ], то ∫ f (x)dx =1, |
|||||
|
|
|
|
|
|
|
α |
|
|
так как вне этого промежутка |
f (x) = 0. |
||||
|
|
|
|||||
33 |
Математическое |
Для ДСВ X равно сумме произведений всех ее зна- |
|||||
|
ожидание |
чений на соответствующие вероятности: |
|||||
|
|
n |
|
|
|
|
|
|
|
M (X ) = ∑xi pi. |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
|
|
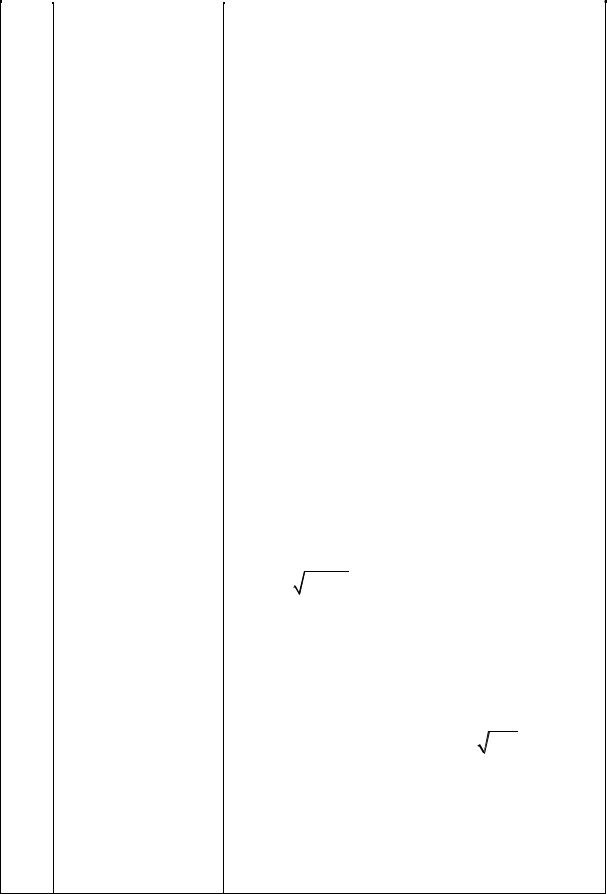
Для НСВ X : M (X ) = ∫ xf (x)dx, |
|||||
|
|
|
|
|
−∞ |
|
|
|
|
где f (x) = F '(x) |
– функция плотности распределе- |
||||
|
|
ния вероятности |
|
|
|
|
|
139
Продолжение прил. Б
№№ |
Понятия, обозначения |
|
|
|
|
Содержание, формула |
|
|
|||||
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
Свойства математиче- |
1) M(C) = C , если C = const, |
|
|
|
|
|
|
|||||
|
ского ожидания |
2) M(CX ) = CM(X), |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
3) M(X + Y) = M(X ) + M(Y), |
|
|
|
|
|
|
|||||
|
|
4) Если X и Y – независимые случайные величины, |
|||||||||||
|
|
то M(XY) = M(X ) M(Y). |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
35 |
Дисперсия случайной |
Разность X − M (X ) называется отклонением слу- |
|||||||||||
|
величины |
чайной величины X от ее математического ожида- |
|||||||||||
|
|
ния M(X ) = a . |
|
|
|
|
|
|
|||||
|
|
Математическое ожидание отклонения равно нулю: |
|||||||||||
|
|
M(X − a) = 0 |
|
|
|
|
|
|
|
|
|||
|
|
Дисперсией, или рассеянием случайной величины |
|||||||||||
|
|
X называется математическое ожидание квадрата ее |
|||||||||||
|
|
отклонения: |
|
|
|
|
|
|
|
|
|||
|
|
D(X ) = M ((X − a)2 ). Следовательно, для любой |
|||||||||||
|
|
случайной величины X : D(X ) ≥ 0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
36 |
Свойства дисперсии |
1) D(C) = 0 , C = const, |
|
|
|
|
|
|
|||||
|
|
2) D(CX ) = C2D(X ), C = const, |
|
|
|
|
|
|
|||||
|
|
3) Если случайные величины X и Y независимы, то |
|||||||||||
|
|
D(X ±Y) = D(X) + D(Y), |
|
|
|
|
|
|
|||||
|
|
4) D(XY) = D(X ) D(Y), |
|
|
|
|
|
|
|||||
|
|
5) D(X ) = M (X 2 ) − (M (X ))2. |
|
|
|
|
|
|
|||||
37 |
Среднеквадратическое |
Среднеквадратическим отклонением, или стандарт- |
|||||||||||
|
отклонение |
ным отклонением, случайной величины X называ- |
|||||||||||
|
|
ется корень квадратный из ее дисперсии: |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
σ (X ) = D(X ) D(X ) = σ 2. |
|
|
|
|
|
|
|||||
38 |
Биномиальное |
Закон распределения дискретной случайной величи- |
|||||||||||
|
распределение |
ны, определяемой формулой Бернулли |
|
|
|||||||||
|
|
p |
k |
= P (k) = Ck pk qn−k (k = 0,1,2,...,n) называ- |
|||||||||
|
|
|
n |
n |
|
|
|
|
|
|
|||
|
|
ется биномиальным. Постоянные n , p называются |
|||||||||||
|
|
параметрами биномиального распределения |
|
|
|||||||||
|
|
(q =1− p). |
|
|
|
|
|
|
|
|
|||
|
|
M (X ) = np; D(X ) = npq;σ (X ) = |
|
|
|
|
|
|
|||||
|
|
|
npq |
|
|
||||||||
|
|
|
|||||||||||
39 |
Распределение |
Распределением Пуассона называется распределе- |
|||||||||||
|
Пуассона |
ние вероятностей дискретной случайной величины, |
|||||||||||
|
|
определяемое формулой Пуассона |
P (k) = |
ake−a |
, |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
n |
k! |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
где a = np – параметр распределения. |
|
|
|||||||||
M(X ) = a;D(X ) = a
140
