
Электротехника
.pdf
3
Тема: «Расчет линейных электрических цепей с использованием законов Ома и Кирхгофа».
Втеории электрических цепей решаются задачи двух типов. К первому типу относятся задачи анализа эл. цепей, когда известна конфигурация цепи, ее элементы, а требуется определить токи, напряжения и мощности тех или иных участков.
Ко второму типу относятся обратные задачи – задачи синтеза эл. цепей, в которых заданы токи и напряжения, а требуется найти конфигурацию цепи и выбрать ее элементы. Следует отметить, что задачи анализа намного проще задач синтеза.
Впрактической электротехнике мы будем рассматривать задачи анализа эл. цепей. Порядок расчета цепей с использованием ЗК:
1.Выбираем произвольные положительные направления токов во всех ветвях эл. схемы.
2.Составить (у-1) уравнение по 1ЗК для токов.
3.Выбираем независимые контуры k = в – у +1.
4.Выбираем произвольные положительные направления обхода независимых контуров.
5.Составляем k уравнений по 2ЗК для напряжений.
6.Решаем систему уравнений (порядка в) и находим Iв.
Поскольку конфигурация цепей может быть достаточно сложной (в>3), то система уравнений, составленная с использованием законов Кирхгофа, может быть достаточно громоздкой. Поэтому для ее решения применяются машинные методы расчета, а уравнения записываются в матричной форме.
1ЗК: |
A×I = 0 |
, где |
|
|||||
1 |
2 |
3 |
в |
|
|
|||
0 |
1 |
−1 |
|
0 |
|
|||
|
0 |
1 |
|
|
1 |
|
- (квадратная) матрица соединений порядка в×(у −1) |
|
A = 0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
1 |
|
0 |
|
|||||
I1
I2
I = I3 - матрица-столбец токов (в)
I4
2ЗК: R × I = E , где

4
|
|
1 |
2 |
3 |
|
m |
|
|
R |
+ |
R |
R |
R |
|
R |
|
|
R = |
1 |
|
2 |
2 |
3 |
|
m |
- матрица сопротивлений порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
R2 |
|
R2+3 |
|
|
|
|
|
|
|
|
Rmk |
||||
m × k
I - матрица-столбец токов (m)
E1
E = E2 - матрица-столбец ЭДС (m).
Em
 Составленные таким образом уравнения будут взаимно независимыми, что в сумме дает необходимое и достаточное количество уравнений для определения m во всех ветвях.
Составленные таким образом уравнения будут взаимно независимыми, что в сумме дает необходимое и достаточное количество уравнений для определения m во всех ветвях.
3.2. Метод контурных токов.
При расчете этим методом составляют систему уравнений по 2ЗК для всех независимых контуров. Затем полагают, что в каждом независимом контуре протекает свой контурный ток Iкк, условное положительное направление которого совпадает с направлением обхода этого контура. Выразив токи в ветвях через контурные токи, получают систему уравнений:
R I |
11 |
+ R I |
22 |
+ + R I |
kk |
= E |
|
|
||||
|
11 |
|
12 |
|
1k |
11 |
|
|||||
R21I11 + R22 I22 |
+ + R2k Ikk |
= E22 |
или в матричном виде: R × I = E |
|||||||||
|
|
|||||||||||
|
|
|||||||||||
R |
I |
11 |
+ R |
I |
22 |
+ + R I |
kk |
= E |
33 |
|
||
|
k1 |
|
k 2 |
|
kk |
|
|
|||||
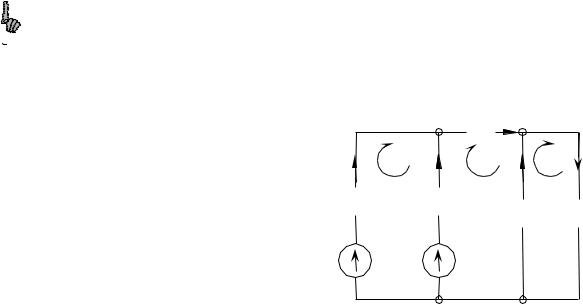
где R11; R22;…Rkk – собственные сопротивления независимых контуров, равные сумме сопротивлений всех резисторов, принадлежащих контуру.
R12=R21; R23=R32 и т.д. – взаимные сопротивления контуров. Это сопротивления резисторов смежных ветвей, принадлежащие как первому, так и второму контурам и т.д.
При этом взаимные сопротивления надо принимать:
А) Положительными, если контурные токи в них направлены одинаково. Б) Отрицательными, если они направлены встречно.
В) Равными нулю, если контуры не имеют общей ветви.
E11, E22, …, Enn – контурные ЭДС, равные алгебраической сумме ЭДС в соответствующих контурах.
5

 Причем ЭДС считают положительными, если их направления совпадают с выбранным направлением обхода контура (контурного тока) и отрицательными, если их
Причем ЭДС считают положительными, если их направления совпадают с выбранным направлением обхода контура (контурного тока) и отрицательными, если их
направление противоположно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
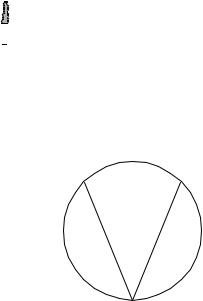
Порядок расчета МКТ |
|
|
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
I3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. |
Выбираем |
условные |
положительные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
I1 |
|
|
|
I11 |
|
|
|
|
I2 |
|
|
I22 I4 |
|
|
|
|
I33 |
|
|
I5 |
|
|
|
|
|||||||||||||
|
направления токов в ветвях. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Выбираем |
k = m − n +1 |
независимых |
|
R1 |
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
R4 |
|
|
|
|
R5 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
контуров. |
|
|
|
|
E1 |
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. |
Выбираем направления обхода контуров, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
совпадающие |
с |
|
условными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
положительными |
|
|
направлениями |
|
|
|
|
|
|
(R1 |
+ R2 )− R2 I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
контурных токов Ikk. |
|
|
|
|
|
|
I11 |
22 |
= |
|
E1 |
− E2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4. |
Составляем систему уравнений по 2ЗК. |
I |
|
(R |
|
R11 |
|
|
|
|
R12 |
|
|
|
|
|
R13 |
=0 E11 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
22 |
|
+ R |
|
+ R ) |
− |
|
R I |
11 |
− R I |
33 |
= |
E |
2 |
||||||||||||||||||||
5. |
Решаем систему относительно контурных |
|
|
2 |
|
3 |
|
4 |
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
токов. |
|
|
|
|
|
|
|
|
|
R22 |
|
|
|
|
|
R21 |
|
|
|
|
|
|
|
R23 |
|
|
|
|
E22 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
+ R5 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
I33 (R4 |
− R4 |
I22 = 0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
6. |
По контурным |
токам |
определяем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E33 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
R33 |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
истинные |
токи ветвей, |
которые равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
R1 + |
R2 |
|
−R2 |
|
|
|
0 |
|
|
|
|
|
|
I11 |
|
E1 −E2 |
|
|||||||||||||||||||||
|
алгебраической сумме контурных токов: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
−R |
|
|
R + |
R |
+ R |
|
|
−R |
|
|
|
× I |
|
= |
|
|
E |
|
|
|
|
||||||||||||||||
|
“+” – если направление совпадает |
|
|
0 |
2 |
|
|
2 |
|
3 |
4 |
R |
|
4 |
|
|
|
|
|
|
|
22 |
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
− |
R |
|
|
|
|
+ R |
|
|
|
|
I |
|
|
|
|
0 |
|
|
|
||||||||||||||
|
“-“ – если оно противоположно |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
5 |
|
|
|
|
|
33 |
|
|
|
|
|
|
|
|
|||||||
|
I1 = I11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
I3 = I22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
I5 = I33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
I2 = I22 − I11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
I4 = I33 − I22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
6
(*) Граф электрической схемы – это условное графическое изображение эл. схемы без указания конкретных элементов, включенных в электрическую схему.
Граф состоит из ветвей и узлов.
Если в ветвях указаны УПН токов, то такой граф называют направленным, иначе – ненаправленным.
(**) Дерево – это путь, соединяющий все узлы без образования контуров.
Все ветви, которые входят в дерево – это ветви дерева, все другие ветви – ветви связи. Независимые контуры образуются путем добавления к дереву по 1 ветви. 
 Следовательно, количество независимых контуров равно количеству ветвей связи.
Следовательно, количество независимых контуров равно количеству ветвей связи.
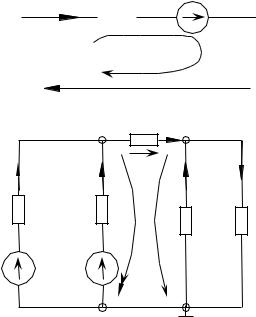
Пример: 1) Эл. схема с 1 станицы.
2) Граф, соответствующей этой электрической схеме.
3
1 2
1 |
2 |
4 |
5 |
3
Лекция № 3
Метод узловых потенциалов.
Метод узловых потенциалов ( МУП ) основан на применении первого закона Кирхгофа и закона Ома. Этот метод особенно эффективен, если число узлов в схеме меньше или равно числу независимых контуров т.е. m ≤ k . В любой электрической схеме потенциал одного из узлов можно принять равным нулю, тогда, число узлов, потенциалы которых необходимо определить относительно этого узла, будет равно (n −1). Следовательно, количество уравнений, необходимых для расчета, равно n −1.
Ток в любой ветви эл. цепи можно определить по известным потенциалам, или направлениями между узлами.
|
I |
R |
|
E |
по 2ЗК ( з-н Ома для уч-ка цепи ) |
в |
|
|
а |
IR +Uab = E; Uab =ϕa −ϕb |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
I =[E − (ϕa −ϕb )]/ R =[E − (ϕa −ϕb )]G |
|
|
|
Uав |
|
|
|
1 |
R3 |
I3 |
2 |
|
I1 |
I2 |
U12 |
|
I4 |
I5 |
R1 |
R2 |
|
|
R4 |
R5 |
|
|
|
|
||
E1 |
E2 |
|
U23 |
|
|
|
|
|
|
||
|
|
U13 |
|
|
|
3
ϕ3 = 0
1у: I1 + I2 − I3 = 0;
2у: I3 + I4 − I5 = 0;
I1 = (E1 −ϕ1 )G1; (U13 =ϕ1 − 0 =ϕ1 ) |
|||||||||||
I2 = (E2 −ϕ1 )G2 ; |
|
|
|
||||||||
I3 = (ϕ1 −ϕ2 )G3; |
|
|
|
|
|||||||
I |
4 |
= (ϕ |
3 |
−ϕ |
2 |
)G |
4 |
= −ϕ |
2 |
G |
; |
|
|
|
|
|
4 |
|
|||||
|
|
=ϕ2G5; |
|
|
|
|
|
|
|
||
I5 |
|
|
|
|
|
|
|
||||
1у: E1G1 −ϕ1G1 + G2 E2 −ϕ1G2 −ϕ1G3 +ϕ2G3 = 0 2у: ϕ1G3 −ϕ2G3 −ϕ2G4 −ϕ2G5 = 0
проведем преобразования:
ϕ1 |
(G1 |
+ G2 + G3 )−ϕ2 G3 = E1G1 |
+ E2G2 |
|
|||||
|
|
|
|
[G]×[ϕ]=[EiGi ] |
|||||
|
G |
|
2 |
G12 |
∑E G |
i |
|||
|
−ϕ1 G3 +ϕ |
(G3 + G4 |
+ G5 ) |
= 0 |
|||||
|
|
11 |
|
|
|
i |
|
||
|
|
|
|
|
|
|
|
||
|
|
G |
21 |
|
G22 |
|
|
|
|
|
|
|
|
|
|
|
|
||
где G11; G22 - сумма проводимостей ветвей, присоединенных к рассматриваемому
узлу;

7
G12 =G21 - сумма проводимостей ветвей, соединяющих соответствующие узлы;
∑Gi Ei - алгебраическая сумма произведений ЭДС ветвей, подходящих к узлу, на
i
проводимости этих ветвей.



 EiGi берется со знаком “+”, если ЭДС направлена к рассматриваемому узлу, и со знаком “-“, если ЭДС направлена от узла ( аналогично, для источника тока ).
EiGi берется со знаком “+”, если ЭДС направлена к рассматриваемому узлу, и со знаком “-“, если ЭДС направлена от узла ( аналогично, для источника тока ).
|
ϕi ∑Gi − ∑ϕ jGij = ∑EiGi + ∑Ji |
|
(1) |
||||
|
i |
j |
i |
i |
|
|
|
|
|
|
|
||||
Если в схеме только два узла, к которым подходят несколько параллельных ветвей, то |
|||||||
основная формула (1) |
значительно |
упрощается |
и |
принимает вид: |
|||
ϕ2 = 0 ϕ1∑Gi = ∑EiGi + ∑Ji |
|
|
|
|
|
||
|
U12 =ϕ1 −ϕ2 =ϕ1 = |
∑EiGi + ∑Ji |
|
(2) |
|||
|
|
|
∑Gi |
|
|
|
|
Метод расчета эл. схем с использованием формулы (2) называется методом двух
узлов.
Зная потенциалы всех узлов схемы по закону Ома находят напряжения и токи ветвях
схемы.

8
Пример: Схема рис. 1. Составим уравнения по законам Кирхгофа:
1у: I1 + I2 − I3 = 0 |
|
|
|
|
|||||
2у: I3 + I4 − I5 = 0 |
|
|
|
|
|||||
|
|
|
|
||||||
Iк: |
R1I1 − R2 I2 = E1 − E2 |
|
|
||||||
|
|
||||||||
IIк: |
R I |
2 |
+ R I |
3 |
− R I |
4 |
= E |
2 |
|
|
2 |
3 |
4 |
|
|
||||
IIIк: |
R4 I4 + R5I5 = 0 |
|
|
|
|
||||
|
|
|
|
||||||
Решением этой
системы из 5 уравнений являются токи 5 ветвей
I1; ; I5
В матричной форме: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
2 |
|
3 |
4 |
5 |
|
I1 |
|
|
|
|
|
|
|
1 |
1 |
|
−1 |
0 |
0 |
|
|
|
0 |
|
|
||||
|
0 |
0 |
|
1 |
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
−1 |
I2 |
|
|
|
|
|
|||||||
R |
− R |
|
0 |
0 |
0 |
|
× I |
3 |
|
= E |
− E |
|
|
||
|
1 |
R2 |
2 |
R3 − R4 |
0 |
|
|
|
|
1 |
E2 |
2 |
|
||
|
0 |
|
|
I4 |
|
|
|
|
|
||||||
|
0 |
0 |
|
0 |
R4 |
|
|
|
|
|
|
|
0 |
|
|
|
|
R5 |
I5 |
|
|
|
|
|
|||||||
Зная токи ветвей, с помощью закона Ома можно определить падения напряжений на различных сопротивлениях ветвей.
Для полной характеристики электрического состояния цепи надо знать не только токи
инапряжения, но также мощности источников и приемников энергии.
Взамкнутой электрической цепи в соответствии с законом сохранения энергии развиваемая источниками энергия равна энергии, потребляемой приемниками. Иначе, алгебраическая сумма мощностей, развиваемых источниками ЭДС и тока, равна сумме мощностей, потребляемых всеми сопротивлениями:
∑Ei Ii + ∑Ui Ji = ∑Ri I 2 - уравнение баланса мощностей.
 Если направление I и E совпадают, то мощность такого источника входит в уравнение с положительным знаком, и источник отдает энергию в цепь ( т.е. работает в режиме генератора ). Если направления ЭДС и тока противоположны, то мощность источника записывается в уравнении со знаком “-“, и такой источник работает в режиме приемника, потребляя энергию.
Если направление I и E совпадают, то мощность такого источника входит в уравнение с положительным знаком, и источник отдает энергию в цепь ( т.е. работает в режиме генератора ). Если направления ЭДС и тока противоположны, то мощность источника записывается в уравнении со знаком “-“, и такой источник работает в режиме приемника, потребляя энергию.
Лекция № 4
Тема: «Гармонические воздействия» Гармонические колебания являются основным видом возмущений и
реакций в энергетических электрических цепях и системах.
Кгармоническим воздействиям относят синусоидальные и
косинусоидальные функции, аргументом которой является время или угол
Θ = wt :
x(t)= Am cos(wt +ϕ0 )= Am cos(Θ +ϕ0 ) или x(t)= Am sin(Θ +ϕ0 ).
Преимущества применения переменного sin тока:
1.Его форма остается неизменной во всех участках сколь угодно сложной эл. цепи. Все устройства, потребляющие эл. энергию, можно включать на любом участке цепи и заранее проектировать их на оптимальный режим работы при данном виде воздействия.
2.Линейная комбинация нескольких гармонических колебаний с одной и той же частотой дает результирующее гармоническое колебание той же частоты.
3.Гармоническая функция является единственной периодической функцией, воспроизводящейся при многократных операциях дифференцирования или интегрирования:
|
d |
A cos(wt +ϕ)= wA |
cos(wt +ϕ + 90°) |
|
||
|
dt |
|
||||
|
m |
|
m |
|
|
|
|
∫Am cos(wt +ϕ)= |
Am |
cos(wt +ϕ − 90°) |
|
||
|
w |
|
||||
4. Простота генерирования |
переменного эл. тока |
в диапазоне |
||||
|
f |
=10 −103 Гц |
электромеханическими |
генераторами. |
||
(подробнее рассмотрены в ЭМ).
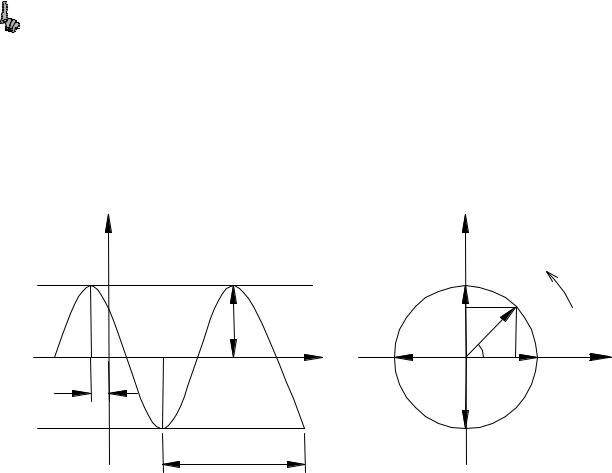
Величины, характеризующие sin ток.
i(t)= Im sin(wt +ϕ0 )
i(t)- мгновенное значение.

1. Im - амплитуда – это абсолютное значение max отклонения sin
процесса от нулевого значения(> 0)
2. T - период – расстояние между 2-мя точками, синусоиды, колеблющимися в одинаковой фазе.
3. Частотой - f = T1 - число периодов изменения за 1 секунду.
4. Угловая частота - w = 2π f - скорость изменения аргумента – угла wt = Θ.
5.Фаза - (wt +ϕ0 ) - это состояние процесса в данный момент времени (аргумент sin ф-ции).
6.Начальная фаза - ϕ0 - это значение фазы при t = 0. Начальная фаза
зависит от выбора начала отсчета времени. она может быть
> 0, < 0, = 0.
Правило знаков: 1. Если в момент времени t = 0 мгновенное
значение sin величины положительно, значит
ϕ0 > 0
2.Аналогично –«»—отрицательно, ϕ0 < 0
3.x(t)= (0,1) ϕ0 = 0
(0,1) ϕ0 = 0
sin cos
При изучении одного установившегося процесса начальная фаза не имеет значения, т.к. всегда можно выбрать момент начала отсчета времени тока, чтобы ϕ0 = 0 . При рассмотрении двух или нескольких процессов таким способом можно выбрать начало отсчета только для одного из них. В таких случаях важным понятием является сдвиг фаз или разность фаз:
∆ϕ = wt +ϕ1 − (wt +ϕ2 )=ϕ1 −ϕ2
При этом изменение начала отсчета одинаково изменяет значения ϕ0 для всех процессов. Поэтому разность фаз не зависит от выбора начала отсчета.
Если ∆ϕ > 0, то колебание x1(t)опережает x2 (t)
Если ∆ϕ < 0, то колебание x1(t)отстает от x2 (t)
2
Если ∆ϕ = 0, то колебание x1(t)находится в фазе с x2 (t)
Если ∆ϕ = ±180°, то колебания x1(t) и x2 (t) находятся в противофазе
Если ∆ϕ = ±90°, то колебания x1(t) и x2 (t) находятся в квадратуре
Векторные диаграммы. ( в.д. )
Наиболее наглядно исследование sin переменных величин (i, u, e) производится применением векторных диаграмм.
Преимущества и особенности использования в.д.
1.Векторные изображения очень наглядны и дают большую экономию в расчетах (также как и методы векторной алгебры по сравнению с аналитическими методами).
2.Применение векторного изображения удобно только для sin токов, т.к. только для них длина вектора (амплитуда) не изменяется во времени.
3.В.д. строятся только для сигналов с равными частотами. В этом случае взаимное расположение векторов остается неизменным, а их
сумма – постоянной.
 4. В.д., являясь удобным геометрическим способом изображения, не указывают направление в пространстве (как это имеет место для векторов напряженности поля, магнитной индукции и т.п.)
4. В.д., являясь удобным геометрическим способом изображения, не указывают направление в пространстве (как это имеет место для векторов напряженности поля, магнитной индукции и т.п.)
Векторы для переменных токов изображают только амплитуды (своей длиной) и их проекции на оси, которые являются мгновенными значениями для
любого момента времени. |
|
|
|
+ j |
|
i(t)= Im cos(wt +ϕ0 ) |
|
|
|||
|
|
|
|
|
t1 |
|
|
Im |
|
|
Im |
|
|
|
t2 |
Im sinθ |
|
t = 0 |
t2 |
|
|
ϕ0 |
|
t1 |
t3 |
t4 |
wt |
|
Im cosθ t4 |
ϕ0 |
|
|
|
|
|
t3 3
T
w
(t = 0)
+1
