
Электротехника
.pdfЛекция №1
Тема: «Основные понятия, определения и законы»
Изучения электрических явлений представляет собой одну из задач физики. Электротехника занимается использованием этих явлений в промышленности и быту, иными словами, ее область – техническое применение электрической энергии, в соответствии с чем технические расчеты составляют основное содержание всех разделов электротехники.
Электрический ток – упорядоченное движение электрических зарядов. Носителями тока в металлах являются электроны, в жидкостях и газах – ионы.
Для количественной оценки тока служит понятие силы тока – количество электричества q, протекающего через поперечное сечение проводника в единицу времени t:
I = qt - если движение зарядов равномерно,
i = dqdt - при неравномерном движении q.
Единица силы – ампер определяется на основании электродинамического взаимодействия проводников, по которым проходит ток. [А]
Ампер – это сила не изменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длинны и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между ними силу, равную 2 10−7 Н/м.
Напряжение – U – скалярная величена, равная работе, которая совершается при перемещении единицы положительного электричества (одного кулона) между двумя точками цепи. [ B = Дж/Кл]
Некоторые примеры значений силы тока.
1.Человек начинает ощущать проходящий через его тело ток, когда сила тока достигает 5 мА.
2.Сила тока люминесцентной лампы 0,15 А = 150 мА; наиболее распространенных ламп накаливания – от 0,2 до 1 А; холодильника – 0,5 - 0,8 А; нагревательных бытовых приборов – 2 - 8 А; электродвигателя трамвайного вагона – от 100 А.
3.Так как заряд электрона очень мал, то даже при малой силе тока в проводнике перемещается очень большое количество электронов. ( e = 16*10-20 Кл ) Так, при едва ощутимом человеком токе силой в 1 мА через тело человека проходит 6*1015 электронов за 1 сек. Если раздать эти электроны всему населению земного шара ( ≈ 3*109 чел), то на долю каждого приходится по 2 миллиона электронов.
Некоторые примеры значений напряжений.
1.Напряжение термоэлементов ( Термо - ЭДС ) – величина порядка десятков мВ; гальванические элементы – дают напряжение немногим более 1 В; в наиболее опасных для человека условиях напряжение электротехнических устройств по отношению к земле не должно превышать 12 В; а в сырых и жарких помещениях – 36 В; напряжение городских осветительных сетей 127 и 220 В; низким напряжением принято считать напряжение между проводником и землей, не превышающее 250 В.
2.Напряжение между контактным проводом и рельсом городского трамвая равно 600 В. Напряжение городских распределительных кабельных сетей обычно 6 или 11 кВ; напряжение между проводами длинных линий электропередач переменного тока 110, 220, 330, 500 и 750 кВ.
3.Напряжение молнии иногда превышает 100 000 кВ.
Электроны, перемещаясь под действием сил электрического поля, сталкиваются с атомами и молекулами проводника, что тормозит их поступательное движение. От формы проводника и структуры его материала зависит, как часто в среднем происходят такие столкновения. Это противодействие проводника направленному движению зарядов, т.е. электрическому току, называется сопротивлением проводника. R [Ом]
Это определение показывает физический смысл сопротивления.
Сопротивление как элемент электрической цепи характеризуется потреблением электрической энергии, т.е. превращением ее в другие виды энергии.
Ток и напряжение на сопротивлении связаны между собой законом Ома (1826г):
I = U |
или |
|
R × I =U |
||
R |
|
|
|
|
|
|
|
U |
|
|
R |
I |
ВАХ |
резистивного |
|
|
линейного элемента |
||
|
|
|
||
U
I
P = I 2 R [Вт]
Электрической цепью называют совокупность устройств и объектов, образующих путь для электрического тока. При этом электромагнитные процессы, протекающие в цепи, могут быть описаны при помощи понятий об ЭДС, токе и напряжении. ( E, I, U ).
Основными элементами электрической цепи являются источники и приемники электрической энергии и провода, соединяющие их между собой. В электрических цепях происходит передача, распределение и взаимное преобразование электрической энергии.
Источники (гальванические элементы, аккумуляторы, генераторы и т.д.).
Химическая энергия
Механическая энергия  Тепловая энергия
Тепловая энергия 
Приемники (эл. лампы, эл. нагревательные приборы, эл. двигатели и т.д. ).
 Тепловая энергия
Тепловая энергия
 Световая энергия
Световая энергия
 Механическая энергия
Механическая энергия
Цепи постоянного тока – это эл. цепи, в которых получение, преобразование и передача энергии происходит при неизменных во времени токах и напряжениях.
Электрическая схема –изображение электрической цепи, содержащее условные графические обозначения ее элементов и способов их соединения.
Электродвижущая сила численно равна разности потенциалов или напряжению между зажимами источника при отсутствии нагрузки, т.е. I = 0.
E |
E =ϕ1 −ϕ2 =U xx (при I=0 ), |
ϕ1 −ϕ2 =U12 |
|
|
|
|
Стрелкой показывают условное положительное |
|
|
направление от большего |
потенциала к |
U |
меньшему. |
|
 Источник ЭДС можно заменить на источник напряжения, при этом условное положительное направление этого источника будет противоположным.
Источник ЭДС можно заменить на источник напряжения, при этом условное положительное направление этого источника будет противоположным.
Любую электрическую цепь упрощенно можно представить эквивалентной схемой электрической цепи.
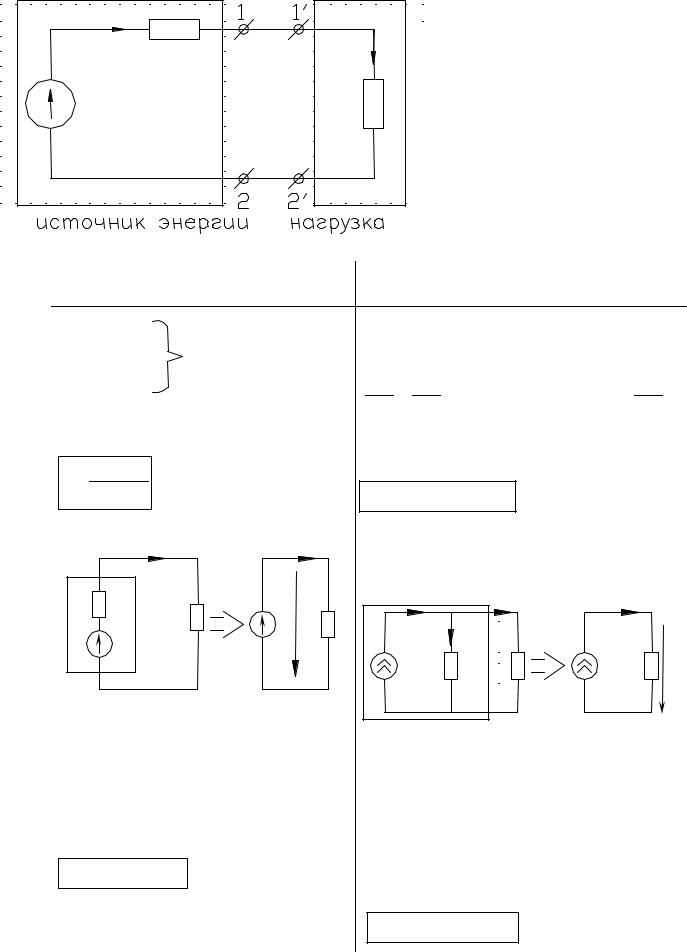
|
|
Rвн |
|
|
|
|
|
Если |
|
к |
|
зажимам |
источника |
|||
|
I |
|
|
I |
присоединить приемник, то в замкну- |
|||||||||||
|
|
|
том контуре возникнет ток. При этом |
|||||||||||||
|
|
|
|
|
||||||||||||
E |
|
|
R |
U12 |
≠ E, так как существует падение |
|||||||||||
|
|
|
|
|
напряжения внутри источника, на его |
|||||||||||
|
|
|
|
|
внутреннем сопротивлении: Uвн=IRвн; |
|||||||||||
|
|
|
|
|
U12=E – IRвн. |
|
|
|
|
|
|
|||||
Источник энергии → Источник ЭДС (U) |
Источник энергии → Источник тока (J) |
|
||||||||||||||
U12=E – IRвн |
т.к. ϕ1 =ϕ2 , ϕ2 =ϕ2 ' |
( ): E = IR + IRвн / : Rвн |
|
|
|
|
|
|||||||||
U1’2’=IR |
то U12 = U1’2’ |
E = U |
+ I =UG |
|
|
+ I , |
где J = E |
- |
||||||||
|
|
|
|
Rвн |
Rвн |
|
|
вн |
|
|
|
Rвн |
|
|||
E – IRвн = IR E = I(R + Rвн) ( ) |
|
|
|
|
|
|
|
|
|
|||||||
ток при к. з. источника энергии, т.е. при U = |
||||||||||||||||
|
|
|
|
|||||||||||||
I = |
E |
- т.е. ток в цепи зависит не |
0, R = 0; I – ток приемника |
|
|
|
|
|||||||||
|
R + Rвн |
|
|
J = UGвн + I = Iвн + I |
|
|
|
|
|
|
||||||
только от R, но и от Rвн |
|
Iвн=UGвн |
– |
|
ток |
равный |
произведению |
|||||||||
|
|
I |
I |
|
||||||||||||
|
|
напряжения на зажимах источника и его |
||||||||||||||
|
|
|
|
|||||||||||||
Rвн |
|
|
E |
проводов. |
|
|
I |
|
|
|
|
|
|
|
||
|
R |
|
|
|
|
|
|
|
|
|
|
|
||||
E |
|
R |
|
J |
|
Iвн |
|
|
|
|
|
J |
|
|||
|
|
J |
|
|
|
|
|
J |
|
|||||||
|
|
|
U |
|
|
|
|
|
|
|
|
R |
|
|||
|
|
|
|
Gвн |
|
|
R |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
Если Rвн<<R и Uвн<<U, то Uвн =IRвн→ |
Если Gвн<<G, Iвн<<I, Iвн=U Gвн → 0. |
|
||||||||||||||
0. Схема идеального источника ЭДС: |
Схема идеального источника тока: |
|
|
|||||||||||||
U=const, при I=var, R=var |
|
J=const; при U,R=var |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
Мощность источника ЭДС: |
|
Мощность источника тока: |
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
E=IRвн+IR (*умножим на I) |
|
J=Iвн+I (*умножим на U) |
|
|
|
|
||||||||||
IE = I 2 R |
+ IU , где |
|
JU = I U + IU =U |
2 / R + IU |
|
|
||||||||||
|
вн |
|
|
|
|
|||||||||||
IE – мощность, развиваемая ист ЭДС |
|
вн |
|
|
|
|
|
|
вн |
|
|
|
||||
I2Rвн |
– мощность потерь |
(например, |
JU =U 2 / R |
+ IU |
|
, где |
|
|
|
|||||||
|
|
|
|
|
|
|
вн |
|
|
|
|
|
|
|
|
|
тепловых в обмотке машины).
IU – мощность, потребляемая нагрузкой, т.е. полезная мощность.
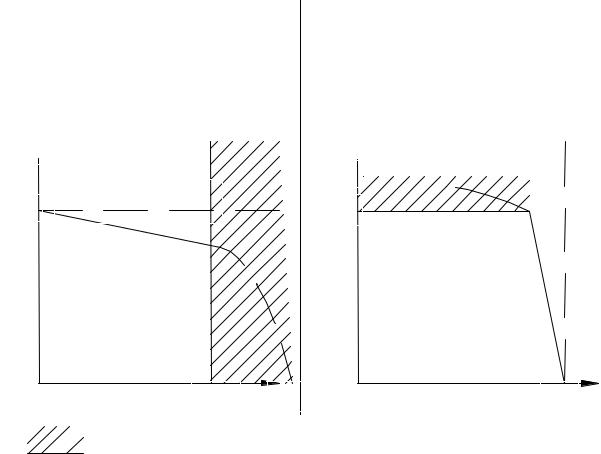
ВАХ источника ЭДС
U 

ВАХ ид. ист. ЭДС
Uxx
Imax Iк.з
JU– мощность, развиваемая источником тока;
U2 / Rвн – мощность потерь на внутреннем сопротивлении (проводимости) источника; IU – полезная мощность.
ВАХ источника тока
U 
Uxx 
Umax тока.ист
ВАХ .ид
I
Iк.з
 - нежелательный режим для источников.
- нежелательный режим для источников.
Вывод:
1) Таким образом, в зависимости от соотношения между внутренним сопротивлением источника энергии Rвн и сопротивлением приемника R, источники энергии могут быть отнесены либо к источникам ЭДС (U ), либо к источникам тока. Однако, при расчетах необходимо учитывать, что тепловые потери у источников различны.
Если Rвн соизмеримо с R можно источник энергии заменить как ист. ЭДС, так и ист. тока. В этом случае Rвн выносят из источника (на схеме) и объединяют с сопротивлением нагрузки R (аналогично для Gвн и G).
Выбор условных положительных направлений для E, I, U:
♦Для источников E, J (см. выше).
♦Для токов – в ветвях с источниками E – совпадающими с направлением ЭДС, во
всех других случаях – произвольно.
♦ Для напряжений – совпадающими с направлениями токов в ветвях или элементе цепи, а на зажимах источника – от “+” к “-“ (см. выше).
1) Если в результате расчета получится отрицательная величина I, то это значит, что действительное направление тока не совпадает с ранее выбранным (т.е. обратно произвольно выбранному положительному направлению).
2)Если в результате расчета получилось, что I и E направлены навстречу друг другу, то это значит, что источник работает в режиме потребителя (например, зарядка аккумуляторной батареи).
Эквивалентные преобразования сопротивлений
1. Последовательное соединение сопротивлений.
|
|
I |
R1 |
|
R2 |
|
|
|
|
|
|
Rn |
|
|
|
|
|
|
|
|
|
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Rэкв = R1 + R2 +... + Rn = ∑Ri |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
U1 |
|
U2 |
|
|
|
|
|
|
Un |
|
|
|
|
|
|
U |
|
i =1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = |
|
; U =U1 +U2 +... +Un |
||||
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rэкв |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2. Параллельное соединение сопротивлений. |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
n |
|||||
|
|
|
I1 |
R1 |
|
= |
+ |
|
+... + |
|
|
; Gэкв = ∑Gi |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Rэкв |
|
R1 |
R2 |
Rn |
i =1 |
||||||||||
|
|
|
I2 |
R2 |
|
|
|
|
|
|||||||||||||||||
|
I |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
In |
|
|
Rn |
|
|
|
I = I1 + I2 + I3 +... + In ; Ui = Ii Ri =U ; I =UGэкв |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
=G [См] |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
P =U 2G [Вт] |
||||||||||||||||
|
|
|
|
|
U |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.Смешанное соединение сопротивлений.
R1 R2 |
R3 |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
I1 |
I3 |
|
RΙ |
= R1 + R2 + R3 + R7 + R8 ; |
||||||||
|
|
|
|
|
|
I2 |
|
||||||||||
U |
R4 |
|
R6 1 |
|
|
|
|
|
|
|
|
|
|||||
R5 |
|
|
= |
1 |
+ |
1 |
+ |
1 |
RΙΙ ; |
Rэкв = RΙ + RΙΙ |
|||||||
|
|
|
|
|
|
||||||||||||
|
R7 |
R8 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
RΙΙ |
|
R4 |
R5 |
R6 |
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Rэкв |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U
При расчете используют метод последовательных преобразований (свертывание) схемы. Полученную схему рассчитывают по закону Ома.
 Во всех случаях замены заданных схем эквивалентными эл. схемами должно выполняться условие: неизменности токов и напряжений в тех частях схемы, которые не затронуты преобразованиями.
Во всех случаях замены заданных схем эквивалентными эл. схемами должно выполняться условие: неизменности токов и напряжений в тех частях схемы, которые не затронуты преобразованиями.
Рассмотрим преобразования соединения « звездой » в соединение « треугольник » и обратно.
|
I |
A |
|
I |
A |
E |
RCA |
RAB |
|
E |
RA |
|
|
||||
|
|
|
|
RC |
RB |
|
|
|
B |
C |
|
|
C |
RBC |
|
B |
|
|
|
|
Условие эквивалентности 

 проще всего определить посредством сопоставления межузловых сопротивлений и проводимостей этих двух схем. Возьмем некоторый источник напряжения и подсоединим его к узлам А и В
проще всего определить посредством сопоставления межузловых сопротивлений и проводимостей этих двух схем. Возьмем некоторый источник напряжения и подсоединим его к узлам А и В 

 , при этом по условию эквивалентности сила тока в обоих случаях должна быть одинаковой, что возможно только при равенстве эквивалентных сопротивлений (проводимостей) между точками А и В:
, при этом по условию эквивалентности сила тока в обоих случаях должна быть одинаковой, что возможно только при равенстве эквивалентных сопротивлений (проводимостей) между точками А и В:
: |
1 |
+ |
|
|
|
1 |
|
|
|
= |
RAB |
+ RBC + RCA |
=G |
|
(AB) |
||||||
|
R |
|
|
R |
+ R |
|
|
|
|
|
|||||||||||
|
|
AB |
|
|
BC |
|
|
R |
AB |
(R |
+ R |
BC |
) |
|
экв |
|
|||||
|
|
|
|
|
|
CA |
|
|
|
|
|
CA |
|
|
|
|
|
||||
|
Rэкв(∆) |
= |
RAB RBC + RAB RCA |
|
|
|
|
|
|
||||||||||||
|
R |
AB |
+ R |
BC |
+ R |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
CA |
|
|
|
|
|
|
||||
 : Rэкв
: Rэкв = RA + RB
= RA + RB
Согласно условию эквивалентности: Rэкв ∆ = Rэкв
RA + RB = |
RAB RBC + RAB RCA = |
RAB RBC + RAB RCA (1) |
|
RAB + RBC + RCA |
∑R∆ |
Аналогично, для узлов B и C, C и A можно получить:
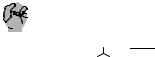
R + R = RBC RCA + RAB RBC (2) |
|
|
||||||||||||
|
B |
|
C |
|
∑R∆ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
R |
|
+ R = RCARBC + RCARAB (3) |
|
|
||||||||||
C |
|
A |
|
∑R∆ |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
Чтобы найти RA : [(1)+ (3)−(2)]/ (2) |
|
|
|
|||||||||||
R |
|
= |
RAB RCA |
; R |
|
= |
RBC RAB |
; R = |
RCARBC |
(4) |
||||
|
A |
|
∑R∆ |
B |
|
∑R∆ |
C |
∑R∆ |
||||||
 Если все три стороны треугольника равны, то сопротивления лучей звезды тоже будут одинаковы R = R3∆
Если все три стороны треугольника равны, то сопротивления лучей звезды тоже будут одинаковы R = R3∆
Обратное преобразование 

 :
:
Если перемножить попарно выражения (4) и сложить:
RARB + RB RC + RC RA = |
RAB RBC RCA |
/ : RC |
|
|
|
|
||||||||||
RAB + RBC + RCA |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
RARB + R |
A |
+ R |
B |
= R |
AB |
; |
RB RC + R |
B |
+ R = R |
BC |
; |
RC RA + R + R |
A |
= R |
(5) |
|
RC |
|
|
|
RA |
C |
|
|
C |
CA |
|||||||
|
|
|
|
|
|
|
|
|
|
|
RB |
|
|
|
||
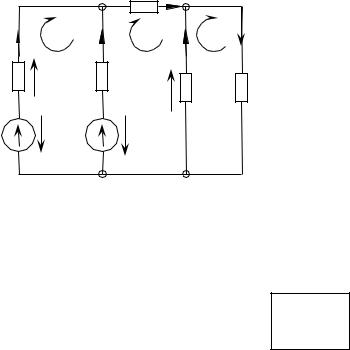
Лекция № 2
Тема: «Топология электрической цепи. Законы Кирхгофа»
Сложная электрическая цепь характеризуется следующими понятиями: ветвь, узел, контур, дерево, независимый контур.
Ветвь – участок электрической цепи, по которому протекает один ток. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Количество ветвей в электрической схеме принято обозначать буквой “в”.
Узел – место соединения трех и более ветвей. Ветви, присоединенные к одной паре узлов, называют параллельными. Напряжение на параллельных ветвях одно и то же. Число узлов будем обозначать буквой “у”.
Контур – любой замкнутый путь, проходящий по нескольким ветвям.
Независимый контур – контур, в состав которого входит хотя бы одна ветвь, не принадлежащая другим контурам. Число независимых контуров обозначим “к”.
k = в - (у - 1) = в – у + 1
|
Рассмотрим пример: |
|
|
|
|
|
|
||
|
|
1 |
R3 |
I3 |
2 |
|
Число ветвей в = 5; |
|
|
I1 |
I |
I2 |
II |
I4 |
III |
I5 |
Число узлов у = 3; |
|
|
Число контуров – 6; |
|
||||||||
|
|
|
|
|
|
|
|
||
R1 |
U1 |
R2 |
U4 |
R4 |
R5 |
Число |
независимых |
контуров |
|
|
|
E2 |
к = в − у +1 = 5 −3 +1 = 3. |
|
|||||
E1 |
|
|
|
|
|
|
|||
U1′ |
U2′ |
|
|
|
Обозначим токи и напряжения. |
|
|||
|
|
|
|
|
|
||||
|
|
3 |
рис 1. |
3 |
|
|
|
|
|
|
Режим электрической цепи произвольной конфигурации полностью определяются |
||||||||
первым и вторым законами Кирхгофа.
Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю.
n
∑Ii = 0
i =1
Правило знаков. При записи уравнений по 1ЗК токи, направленные к узлу будем брать со знаком “+”, от узла – со знаком “-“.
1 узел: I1 + I2 − I3 = 0 .
2
Второй закон Кирхгофа:
Формулировка 1: В любом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на сопротивлениях, входящих в этот контур.
∑Ei = ∑Ri Ii
i i
Формулировка 2: Алгебраическая сумма напряжений на всех элементах замкнутого контура (включая источники ЭДС) равна нулю.
∑Ui = 0
i
Например (после правил составления уравнений). I контур: R1I1 − R2 I2 = E1 − E2
т.к. U ' |
= −E , U ' |
= −E |
2 |
, то |
R I |
1 |
− R I |
2 |
+U ' |
−U ' |
= 0 |
|
1 |
1 |
2 |
|
|
1 |
2 |
2 |
1 |
|
|||
Порядок составления уравнений. Для записи уравнений по 2ЗК необходимо:
1.Задать условные положительные направления E, I, U.
2.Выбрать направление обхода контура, для которого записывается уравнение.
3.Записать уравнение, пользуясь одной из формулировок, причем слагаемые, входящие в уравнения берут со знаком “+”, если их условные положительные
направления совпадают с направлением обхода контура, и со знаком “-“ если они противоположны.



 2ЗК можно пользоваться для определения напряжения между двумя произвольными точками схемы. Для этого необходимо ввести в схему напряжение между этими точками,
2ЗК можно пользоваться для определения напряжения между двумя произвольными точками схемы. Для этого необходимо ввести в схему напряжение между этими точками,
которое как бы дополняет незамкнутый контур до замкнутого. |
|
||||||
Пример: |
R1 |
I |
R2 |
- |
E |
|
|
|
|
|
|||||
а |
|
+ в Uва =ϕв |
−ϕа |
||||
|
|
|
|
||||
|
|
|
|
|
|||
U1 |
U2 |
U3 |
R1I + R2 I +Uва = E |
||||
|
|
|
|
U |
ва |
= E − I(R |
+ R ) или |
|
|
|
|
|
1 |
2 |
|
|
Uва |
|
|
|
|
R1I + R2 I −U3 +Uва = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
т.к.U3 = E, тоUва =U3 − I(R1 + R2 ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
численно |
|
|
|
|
|
|
|
Uва = E − I(R1 + R2 ) |
|
|
|
|
|
|
|
||
