Zadania_k_sem_rab__1_po_fizike

Семестровая работа №1

Таблица 1.

№	№ задачи
варианта	1	2	3	4	5	6	7	8
1	1	21	41	51	71	91	111	131
2	2	22	42	52	72	92	112	132
3	3	23	43	53	73	93	113	133
4	4	24	44	54	74	94	114	134
5	5	25	45	55	75	95	115	135
6	6	26	46	56	76	96	116	136
7	7	27	47	57	77	97	117	137
8	8	28	48	58	78	98	118	138
9	9	29	49	59	79	99	119	139
10	10	30	50	60	80	100	120	140
11	11	31	41	61	81	101	121	131
12	12	32	42	62	82	102	122	132
13	13	33	43	63	83	103	123	133
14	14	34	44	64	84	104	124	134
15	15	35	45	65	85	105	125	135
16	16	36	46	66	86	106	126	136
17	17	37	47	67	87	107	127	137
18	18	38	48	68	88	108	128	138
19	19	39	49	69	89	109	129	139
20	20	40	50	70	90	110	130	140

1. Две автомашины движутся по дорогам, угол между которыми =60°. Скорость автомашин 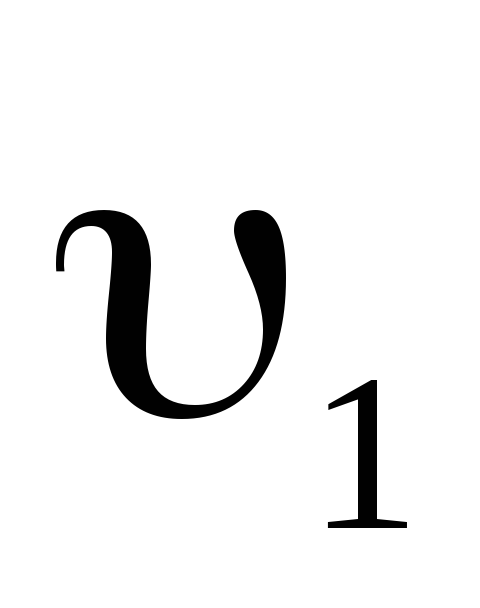=54 км/ч и 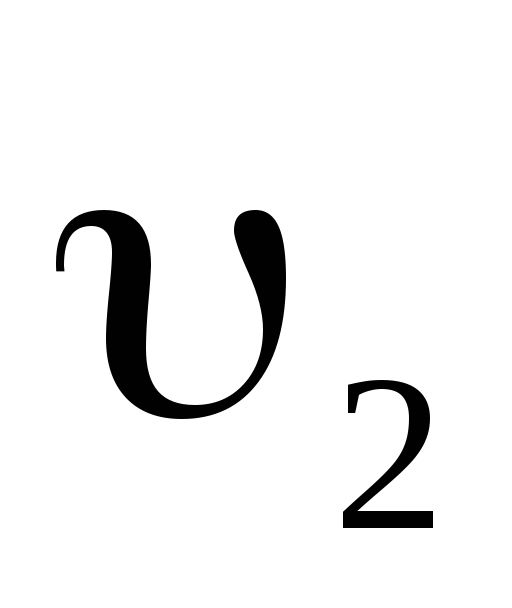=72 км/ч. С какой скоростью и удаляются машины одна от другой?

2. Материальная точка движется прямолинейно с начальной скоростью 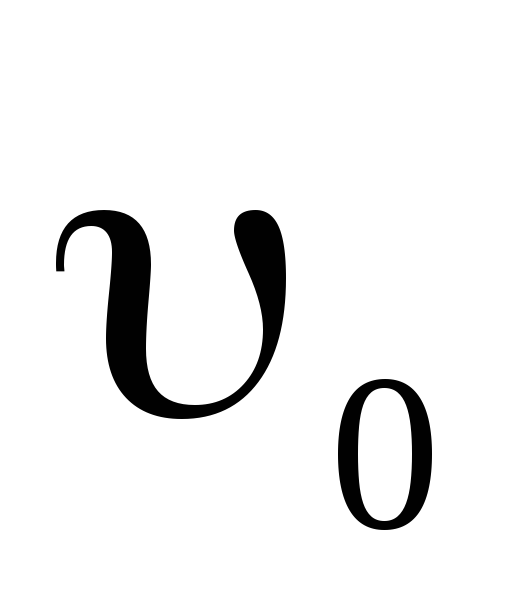=10 м/с и постоянным ускорением а=-5м/с². Определить, во сколько раз путь s, пройденный материальной точкой, будет превышать модуль ее перемещения r спустя t=4 с после начала отсчета времени.

3. Тело брошено горизонтально с начальной скоростью 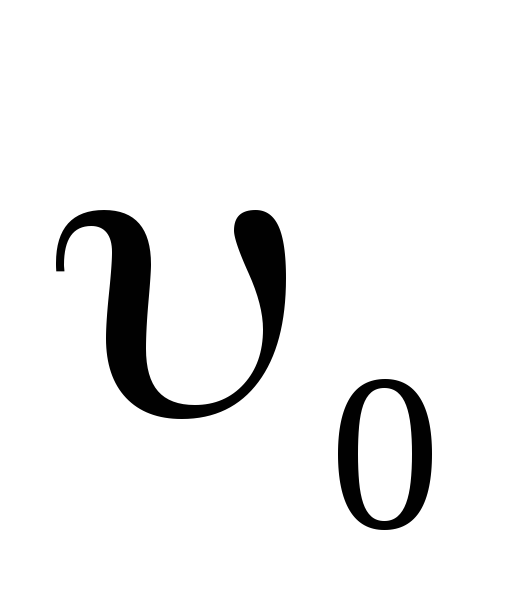=10 м/с. Через =2 с после начала движения, пренебрегая сопротивлением воздуха, найти: а) угол между вектором скорости и вертикалью; б) модули тангенциального и нормального ускорений; в) радиус кривизны траектории в точке, соответствующей этому моменту времени.

4. Движение точки по окружности радиуса R=4 м задано уравнением s=A+Bt+Ct², где A=10 м, В=-2 м/с, С=1 м/с². Найти тангенциальное а_, нормальное a_n и полное а ускорение точки в момент времени t=2с.

5. По дуге окружности радиуса R=10 м движется точка. В некоторый момент времени нормальное ускорение точки a_n=4,9 м/с²; вектор полного ускорения образует в этот момент с вектором нормального ускорения угол =60⁰. Найти скорость и тангенциальное ускорение а_ точки.

6. Точка движется по окружности радиуса R=2 м согласно уравнению s=At³, где A=2м/с³. В какой момент времени t нормальное ускорение а_n точки будет равно тангенциальному а_. Чему будет равно полное ускорение a в этот момент времени?

7. Движение точки по кривой задано уравнениями x=A₁t³, где A₁=l м/c³ и y=A₂t, где A₂=2 м/с. Найти уравнение траектории точки, ее скорость и ускорение а в момент времени t=0,8 с.

8. Пистолетная пуля пробила два вертикально закрепленный листа бумаги, расстояние между которыми l=30 м. Пробоина во втором листе оказалась на h=10 см ниже, чем в первом. Определить скорость пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

9. Тело брошено под углом =30° к горизонту со скоростью 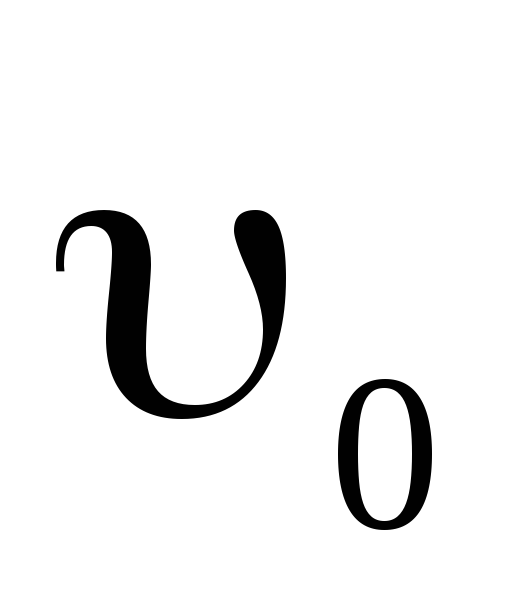=30 м/с. Каковы будут нормальное а_n и тангенциальное a_ ускорения тела через время t=1c после начала движения?

10. Тело брошено под некоторым углом  к горизонту. Найти величину этого угла, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты Н траектории.

11. Камень брошен с вышки в горизонтальном направлении со скоростью 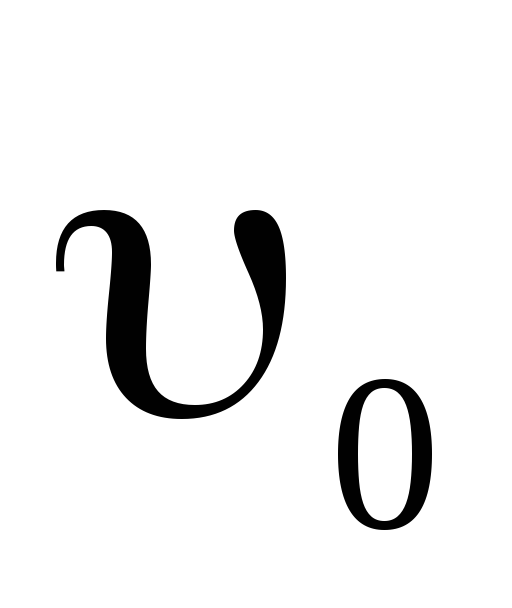=30 м/с. Определить скорость , тангенциальное а_ и нормальное а_n ускорения камня в конце второй секунды после начала движения.

12. Тело брошено под углом =30° к горизонту. Найти тангенциальное а_ и нормальное а_n ускорения в начальный момент движения.

13. Небольшое тело начинает движение по окружности радиусом R=30 м с постоянным по модулю тангенциальным ускорением а_=5 м/с². Найти полное ускорение тела через =3 с после начала движения.

14. Материальная точка движется по окружности радиусом R=5 м. Когда нормальное ускорение точки становится a_n=3,2 м/с, угол между векторами полного и нормального ускорений =60°. Найти модули скорости и тангенциального ускорения точки для этого момента времени.

15. Нормальное ускорение частицы, движущейся по окружности радиусом R=3,2 м, изменяется по закону а=At², где А=2,5 м/с⁴. Найти: а) путь, пройденный частицей за =5 с после начала движения; б) тангенциальное и полное ускорения в конце этого участка пути.

16. Автомобиль, движущийся со скоростью =54 км/ч, проходит закругление шоссе радиусом кривизны R=375 м. На повороте шофер тормозит машину, сообщая ей ускорение а_=0,5 м/с². Найти модули нормального и полного ускорений автомобиля на повороте и угол между их направлениями.

17. Точка движется по окружности так, что зависимость пути от времени описывается уравнением s=Bt+Ct², где В=-2 м/с, С=2 м/с². Через t₁=1 с после начала движения нормальное ускорение точки а_n=0,5 м/с². Найти время , при котором модули нормального и тангенциального ускорения будут равны.

18. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t=3 с опустился на А=1,5 м. Определить угловое ускорение  цилиндра, если его радиус r=4 см.

19. Диск радиусом r=10 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением =0,5 рад/с². Каковы были тангенциальное а_, нормальное а_n и полное а ускорения точек на окружности диска в конце второй секунды после начала вращения?

20. Диск радиусом r=20 см вращается согласно уравнению =A+Вt+Сt³, где A=3 рад, B=-1 рад/с, С=0,1 рад/с³. Определить тангенциальное а_, нормальное a_n и полное а ускорения точек на окружности диска для момента времени t=10 c.

    21. Наклонная плоскость, образующая угол =25° с плоскостью горизонта, имеет длину l=2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за время t=2 с. Определить коэффициент трения тела о плоскость.

    22. Материальная точка с массой m=2 кг двигается под действием некоторой силы согласно уравнению x=A+Bt+Ct²+Dt³, где С=1 м/с², D=-0,2 м/с³. Найти значение этой силы в момент времени t₁=2 с и t₂=5 с. В какой момент времени сила равна нулю?

    23. Молот массой m=1 т падает с высоты h=1,77 м на наковальню. Длительность удара t=0,01 с. Определить среднее значение силы <F> удара.

    24. Шайба, пущенная по поверхности льда с начальной скоростью 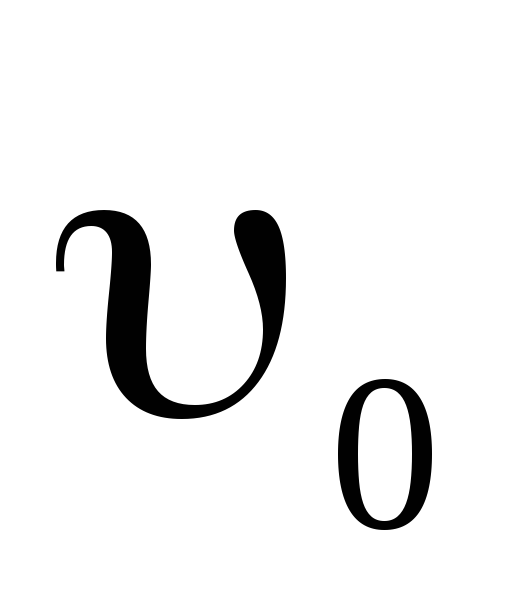=20 м/с, остановилась через t=40 с. Найти коэффициент трения шайбы о лед.

    25. Материальная точка массой m=1 кг, двигаясь равномерно, описывает четверть окружности радиуса r=1,2 м в течение времени t=2 с. Найти изменение импульса точки.

    26. Тело массой m=5 кг брошено под углом =30° к горизонту с начальной скоростью 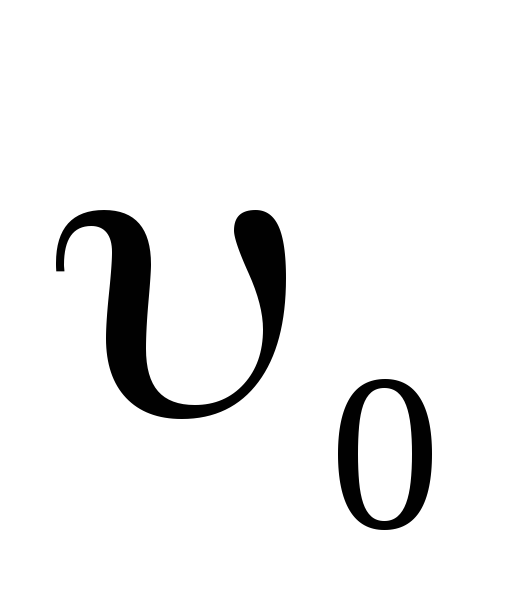=20 м/с. Пренебрегая сопротивлением воздуха, найти: 1) импульс силы F, действующей на тело, за время полета тела; 2) изменение импульса тела за время полета. Сравнить найденные величины между собой.

    27. Шарик массой m=100 г упал с высоты h=2,5 м на горизонтальную плиту, масса которой много больше массы шарика, и отскочил от нее вверх. Считая удар абсолютно упругим, определить импульс р, полученный плитой.

    28. Шарик массой m=300 г ударился о стену и отскочил от нее. Определить импульс p₁, полученный стеной, если в последний момент перед ударом шарик имел скорость =10 м/с, направленную под углом =30° к поверхности стены. Удар считать абсолютно упругим.

    29. Тело массой m=0,2 кг соскальзывает без трения по желобу высотой h=2 м. Начальная скорость шарика 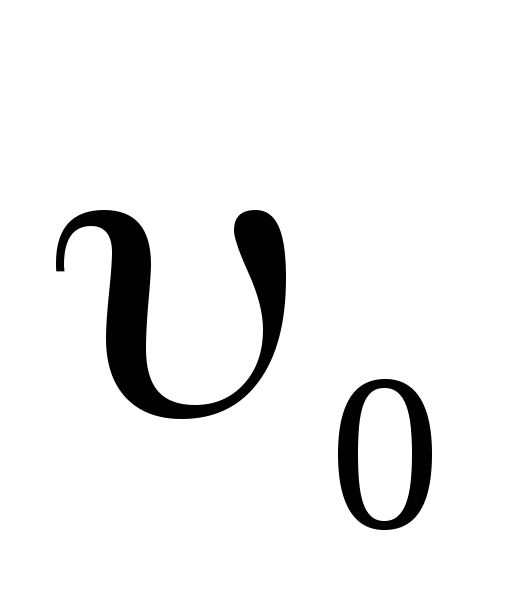=0. Найти изменение р импульса шарика и импульс р, полученный желобом при движении тела.

    30. Ракета массой m=1 т, запущенная с поверхности Земли вертикально вверх, поднимается с ускорением a=2g. Скорость струи, газов, вырывающихся из сопла, 1200 м/с. Найти расход m₁ горючего.

    31. Космический корабль имеет массу m=3,5 т. При маневрировании из его двигателей вырывается струя газов со скоростью =800 м/с; расход горючего m₁=0,2 кг/с. Найти реактивную силу R двигателей и ускорение а, которое она сообщает кораблю.

    32. Вертолет с ротором, диаметр которого d=18 м и масса m=3,5 т, «висит» в воздухе. С какой скоростью и ротор отбрасывает вертикально вниз струю воздуха? Диаметр струи считать равным диаметру ротора.

    33. Брусок массой m₂=5 кг может свободно скользить по горизонтальной поверхности без трения. На нем находится брусок меньшей массы m₁=l кг. Коэффициент трения соприкасающихся поверхностей брусков k=0,3. Определить максимальное значение силы, приложенной к нижнему бруску, при которой начнется соскальзывание верхнего бруска.

    34. На горизонтальной поверхности находится брусок массой m=2 кг. Коэффициент трения бруска о поверхность k₂=0,2. На бруске находится другой брусок массой m₁=8 кг. Коэффициент трения верхнего бруска о нижний k₁=0,3. К верхнему бруску приложена сила F. Определить: 1) при каком значении силы F₁ начнется совместное скольжение брусков по поверхности; 2) при каком значении силы F₂ верхний брусок начнет проскальзывать относительно нижнего.

    35. Ракета, масса которой М=6 т, поднимается вертикально вверх. Двигатель ракеты развивает силу тяги F=500 кН. Определить ускорение ракеты и натяжение троса, свободно свисающего с ракеты на расстоянии, равном 1/4 его длины от точки прикрепления троса. Масса троса m=10 кг. Силой сопротивления воздуха пренебречь.

    36. Через невесомый блок, подвешенный к пружинным весам, перекинута легкая нерастяжимая нить, к концам которой прикреплены грузы массами m₁=0,5 кг и m₂=0,6 кг. Что покажут весы во время движения грузов, если пренебречь трением в оси блока?

    37. Мотоциклист делает поворот на горизонтальной поверхности по дуге радиусом кривизны R=80 м. Коэффициент трения колес о почву =0,4. Найти: а) максимальную скорость, которую может развить мотоциклист на повороте; б) угол, на который он должен накрениться, чтобы не упасть.

    38. Тяжелый шарик, подвешенный на легкой нерастяжимой нити длиной l=0,5 м, вращается в горизонтальной плоскости. Нить образует с вертикалью угол =30°. Найти период вращения шарика.

    39. Через неподвижный блок перекинута тонкая нерастяжимая нить, на концах которой подвешены два груза массами m₁=200 г и m₂=300 г. Какой путь пройдет каждый из грузов за 1с? Считать, что блок вращается без трения. Массой блока пренебречь.

    40. Какое наибольшее ускорение может развить автомобиль при движении вверх по наклонной дороге с углом наклона =20°, если коэффициент трения колес о покрытие дороги =0,5? Какой путь пройдет автомобиль за t=10 с, если в момент начала подъема скорость его 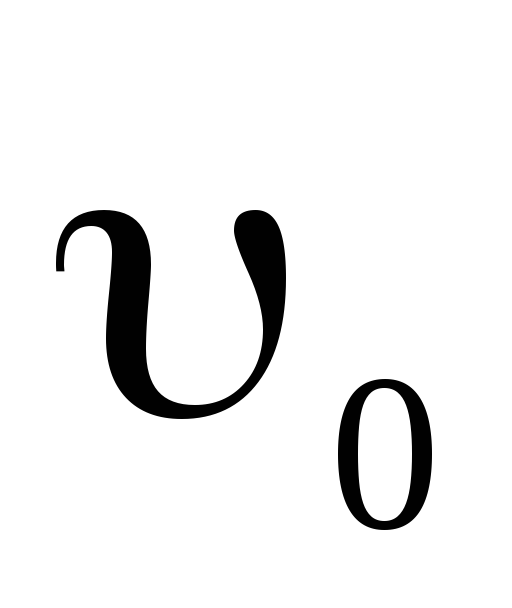=10 м/с?

    41. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m₁=60 кг, масса доски m₂=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) =1 м/с? Массой колес и трением пренебречь.

42. На сколько переместится относительно берега лодка длиной l=3,5 м и массой m₁=200кг, если стоящий на корме человек массой m₂=80кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.

43. Лодка длиной l=3 м и массой m=120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m₁= 60 кг и m₂=90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?

44. В лодке массой m₁=240 кг стоит человек массой m₂=60 кг. Лодка плывет со скоростью =2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью =4 м/с (относительно лодки). Найти скорость движения лодки после прыжка человека: 1) вперед по движению лодки и 2) в сторону, противоположную движению лодки.

45. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека М=60 кг, масса доски m=20 кг. С какой скоростью u (относительно пола) будет двигаться тележка, если человек пойдет вдоль доски со скоростью (относительно доски) =1 м/с? Массой колес пренебречь. Трение во втулках не учитывать.

46. На платформе установлена безоткатная пушка, из которой производится выстрел вдоль железнодорожного пути под углом 45° к горизонту. Определить начальную скорость снаряда, если известно, что после выстрела платформа откатилась на расстояние 3,0 м. Масса платформы с пушкой М=2,0∙10⁴ кг, масса снаряда m=10 кг, коэффициент трения качения между колесами платформы и рельсами =0,002.

47. Граната брошена под углом 45° к горизонту со скоростью =20 м/с. Через 2,0 с после момента бросания граната разрывается на два осколка, массы которых относятся как 1:2. Меньший осколок в результате взрыва получил дополнительную скорость =50 м/с, направленную горизонтально вдоль направления бросания гранаты. Определить дальность полета большего осколка, если известно, что меньший осколок упал на расстояние s₁=83 м. Сопротивление воздуха не учитывать.

48. Шар массой m₁=4 кг движется со скоростью =5 м/с и сталкивается с шаром массой m₂=6 кг, который движется ему навстречу со скоростью =2 м/с. Определить скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

49. Человек массой m₁=70 кг, бегущий со скоростью =9 км/ч, догоняет тележку массой m₂=190 кг, движущуюся со скоростью =3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?

50. Конькобежец, стоя на коньках на льду, бросает камень массой m₁=2,5 кг под углом =30° к горизонту со скоростью =10 м/с. Какова будет начальная скорость движения конькобежца, если масса его m₂=60 кг? Перемещением конькобежца во время броска пренебречь.

51. В деревянный шар массой m₁=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля массой m₂=4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол =3°? Размером шара пренебречь. Удар пули считать прямым, центральным.

52. По небольшому куску мягкого железа, лежащему на наковальне массой m₁=300 кг, ударяет молот массой m₂=8 кг. Определить КПД  удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.

53. Из ствола автоматического пистолета вылетела пуля массой m₁=10 г со скоростью =300 м/с. Затвор пистолета массой m₂=200 г прижимается к стволу пружиной, жесткость которой k=25 кН/м. На какое расстояние отойдет затвор после выстрела? Считать, что пистолет жестко закреплен.

54. Шар массой m₁=5 кг движется со скоростью =1 м/с и сталкивается с покоящимся шаром массой m₂=2 кг. Определить скорости u₁ и u₂ шаров после удара. Удар считать абсолютно упругим, прямым, центральным.

55. Из шахты глубиной h=600 м поднимают клеть массой m₁=3,0 т на канате, каждый метр которого имеет массу m=1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия  подъемного устройства?

56. Пружина жесткостью k=500 Н/м сжата силой F=100 H. Определить работу А внешней силы, дополнительно сжимающей пружину еще на l=2 см.

57. Какую нужно совершить работу А, чтобы пружину жесткостью k=800 Н/м, сжатую на х=6 см, дополнительно сжать на x=8 см?

58. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на l=3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h=8 см?

59. Из пружинного пистолета с пружиной жесткостью k=150 Н/м был произведен выстрел пулей массой m=8 г. Определить скорость и пули при вылете ее из пистолета, если пружина была сжата на х=4 см.

60. Налетев на пружинный буфер, вагон массой m=16 т, двигавшийся со скоростью =0,6 м/с, остановился, сжав пружину на l=8 см. Найти общую жесткость k пружин буфера.

61. Цепь длиной l=2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает l/3, то цепь соскальзывает со стола. Определить скорость v цепи в момент ее отрыва от стола.

62. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h=40 м, наружным диаметром D=3,0 м и внутренним диаметром d=2,0 м? Плотность материала  принять равной 2,8∙10³ кг/м³.

63. Однородная тяжелая гибкая нить длиной l лежит на наклонной плоскости призмы, расположенной под углом  к горизонту, а один конец нити свисает вдоль вертикальной грани призмы. При какой наименьшей длине свисающей части нить начнет скользить, сползая с призмы, если коэффициент трения ?

64. Однородная цепь лежит на горизонтальной поверхности стола, и при этом один ее конец свисает со стола. Определить коэффициент трения, если известно, что цепь начинает соскальзывать со стола, когда длина свисающего конца составляет 1/6 часть общей длины цепи.

65. Молоток массой 0,80 кг в, момент удара о шляпку гвоздя имеет скорость 1,5 м/с и забивает его в бревно на глубину 5,0 мм. Какой массы груз необходимо положить на шляпку гвоздя, чтобы он вошел в бревно на такую же глубину?

66. Тело массой m=500 г, прикрепленное к резиновому шнуру длиной l₀=9,5 см, отклоняют на угол =90° и отпускают. Коэффициент жесткости резинового шнура k=9,8 Н/см. Найти длину l резинового шнура в момент прохождения телом положения равновесия.

67. Груз, положенный на чашку весов, сжимает пружину на х₁=5 см. Найти величину сжатия пружины для случая, когда этот же груз падает на чашку весов с высоты h=10 см.

68. С какой наименьшей высоты h должен начать скатываться акробат на велосипеде (не работая ногами), чтобы проехать по дороже, имеющей форму «мертвой петли», радиусом r=4 м и не оторваться от дорожки в верхней точке петли? Трением пренебречь.

69. В баллистический маятник массой М=5 кг попала пуля массой m=10 г и застряла в нем. Найти скорость пули, если маятник, отклонившись после удара, поднялся на высоту h=10см.