3.3 Экспоненциальное распределение

Для получения случайных величин, распределенных по экспоненциальному закону, используем имеющуюся таблицу и воспользуемся формулой (6). Примем b=1. Запишем в ячейку С2 название переменнойЕ, а в ячейку С4 выражение =-LN(B4) и скопируем его до ячейки С103. Если в таблице произошли изменения адресов ссылок, то в строке 3 восстановить возрастание номеров от 1 до 13, проверить выражение в ячейкеD4, которое должно иметь вид: =ЕСЛИ(И($C4>=((A$3-1)*$C$106+$C$104);$C4<=(A$3*$C$106+$C$104));1), при необходимости внести изменения и скопировать его до ячейки М103. Нажимая клавишуF9, наблюдать изменение графиков.

Зарисовать два графика экспоненциального распределения в соответствии с примером, приведенным на рис. 4.

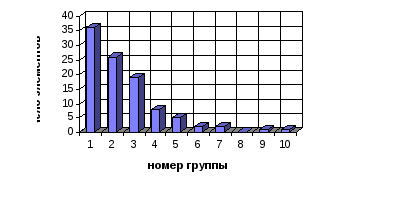
Рис. 4. Экспоненциальное распределение случайных величин

3.4 Равновероятное распределение

Для получения случайных величин, имеющих равновероятное распределение, используем имеющуюся таблицу. Перенесем содержимое ячеек В104-В107 в ячейки А104-А107 и скопируем выражения из ячеек С104-С106 в ячейки В104-В106. Удалим столбец С, в строке 3 восстановим возрастание номеров от 1 до 12 и исправим содержимое ячейки С4, записав в нее выражение =ЕСЛИ(И($B4>=((A$3-1)*$B$106+$B$104);$B4<=(A$3*$B$106+$B$104));1) и скопируем его до ячейки L103. Нажимая клавишуF9, наблюдать изменение графиков.

Зарисовать два графика равновероятного распределения в соответствии с примером, приведенным на рис. 5.

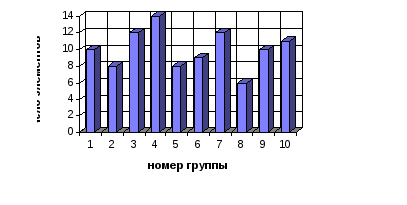
Рис. 5. Равновероятное распределение случайных величин

4. Содержание отчета

1. Цель работы.

2. Формулы генерирования случайных чисел для заданного закона распределения.

3. Гистограммы распределения по группам случайных величин.

4. Выводы и заключение по выполненной работе.

5. Контрольные вопросы

1. Основные понятия моделирования.

2. Требования, предъявляемые к моделям.

3. Классификация технических систем.

4. Классификация моделей.

5. Метод имитационного моделирования.

6. Моделирование случайных чисел с заданным законом распределения случайных величин.

7. Принципы построения имитационных моделирующих алгоритмов.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Соболь И. М. Метод Монте-Карло.–М.: Наука, 1978.–64 с.

2. Лукьянов В. С. Решение задач в машиностроении методами имитационного моделирования. Учебное пособие. Волгоград. Изд. ВолгПИ, 1989, 26 с.

3. Бусленко Н. П. Моделирование сложных систем.–М.: Наука, 1978.–310 с.

4. Советов Б. Я., Яковлев С. А. Моделирование систем.–М.: Наука, 1998.–146 с.

5. Основы моделирования сложных систем/ Под ред. Л. И. Дыхненко.–Киев: Технiка, 1981.–359 с.

6. Основы моделирования сложных систем/ Под ред. В. В. Налимова.–М.: Высш. шк., 1981.–358 с.

7. Таха Х. Введение в исследование операций: В 2-х книгах. Кн. 2.–М.: Мир, 1985.–496 с.

8. Прицкер А. Введение в имитационное моделирование и язык СЛАМ II.–М.: Мир, 1987.–646 с.

Составители Аркадий Георгиевич Кесоян

Леонид Абрамович Рабинович

МОДЕЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА

Методические указания к лабораторной работе

по дисциплине «Моделирование систем»

Темплан 2005 г., поз. № 52

Подписано в печать 10.02.2005. Формат 60 х84 1/16.

Бумага газетная. Печать офсетная. Усл. печ. л. 0,7

Тираж 100 экз. Заказ. . Бесплатно.

Волгоградский государственный технический университет.

400131 Волгоград, просп. им. Ленина, 28

РПК “Политехник” Волгоградского государственного технического университета

400131 Волгоград, ул. Советская, 35