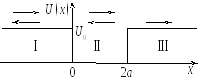Федеральное агентство по образованию

Волгоградский государственный технический университет

Кафедра “Экспериментальная физика”

ИЗУЧЕНИЕ ЭФФЕКТА РАМЗАУЭРА

Методические указания

к лабораторной работе №509

Волгоград

2009

УДК 53 (075.5).

Изучение эффекта Рамзауэра: метод. указ. к лабораторной работе №509/ сост. А.В. Аршинов, В.Н. Перминов; Волгоград. гос. техн. ун-т. – Волгоград, 2009. – 12 с.

Cодержат основные сведения и рекомендации по выполнению лабораторной работы №509, представленной в практикуме кафедры экспериментальной физики Волгоградского государственного технического университета.

Предназначены для студентов всех форм обучения.

Ил. 6. Табл. 1. Библиогр.3: назв.

Рецензент: кандидат физико-математических наук,

доцент кафедры «Физика»

Волгоградского государственного технического университета

Гудилов С.М.

Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета

© Волгоградский

государственный

технический

университет, 2009.

ИЗУЧЕНИЕ ЭФФЕКТА РАМЗАУЭРА

1. Цель работы

1) Изучить эффект Рамзауэра; 2) определить критические значения энергии электронов, соответствующих максимуму и минимуму прозрачности атома ксенона; 3) вычислить ширину и глубину потенциальной ямы, а также потенциал ионизации атома ксенона.

2. Содержание работы

В квантовой физике состояние частицы описывается волновой функцией, квадрат модуля которой определяет плотность вероятности нахождения частицы в заданной области пространства. Волновая функция должна быть непрерывной, конечной, однозначной, и иметь непрерывную первую производную.

Волновая функция может быть найдена из решения уравнения Шредингера:

.

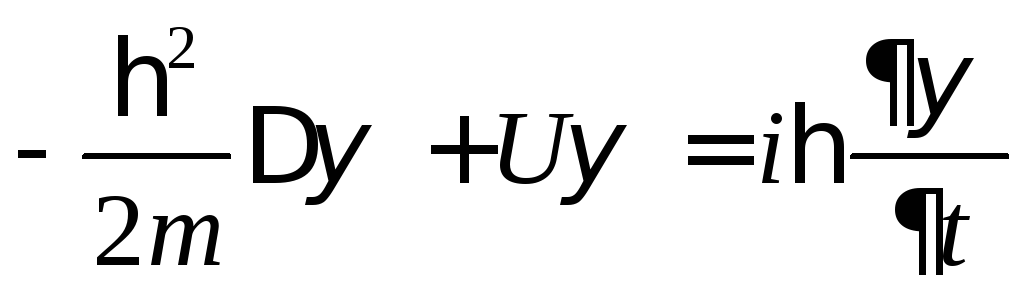Особый интерес представляет стационарное уравнение Шредингера:

,

где ,– потенциальная энергия частицы в данной области пространства,– полная энергия частицы.

Рассмотрим случай, когда частица (в нашем случае – электрон) находится в области пространства, содержащей одномерную потенциальную яму высотой и шириной(рис. 1). Для этой области распределение потенциальной энергии описывается функцией:

Рис. 1. Одномерная потенциальная яма

В областях пространства I и III уравнение Шредингера имеет вид:

, (1)

где . В областиII уравнение Шредингера имеет вид:

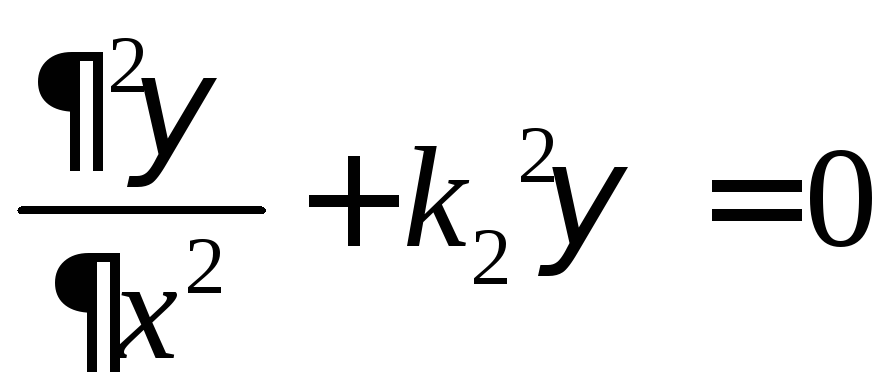, (2)

где .

Решениями уравнений (1) и (2) для областей I, II, и III являются соответственно

,

,

,

где коэффициенты описывают амплитуду падающей на «барьер» волны вi-ой области, коэффициенты – амплитуду отраженной волны (соответствующие волны на рис. 1 указаны стрелками).

Коэффициенты иможно определить из свойства непрерывности волновой функции на границе между соседними областями:

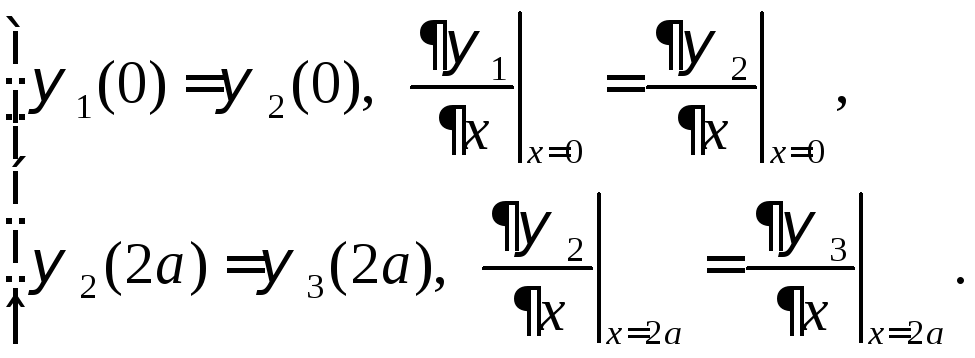(3)

Подстановка выражений для волновых функций каждой из областей в систему уравнений (3) позволяет определить коэффициент отражения волны от потенциальной ямы в виде

. (4)

Анализ выражения (4) показывает, что коэффициент отражения будет стремиться к нулю, если энергия электрона значительно превышает потенциальный барьер (). Однакоможет обратиться в ноль и при меньших значениях энергии, когда выполняется равенство

, (5)

где – целое число. В этом случае на ширине ямыукладывается целое число полуволн. Две волны, отраженные от краев ямы, гасят друг друга, и электрон пролетает областьII свободно, не испытывая отражения.

Полученный результат объясняет так называемый эффект Рамзауэра, наблюдаемый при упругом рассеянии электронов на атомах благородных газов: аргона, криптона и ксенона. Он заключается в том, что вероятность рассеяния резко уменьшается при некоторых значениях энергии электрона.

Вероятность рассеяния электронов на атомах характеризуется эффективным сечением рассеяния , которое численно равно площади круга с центром в ядре атома, при попадании в который электрон отклоняется от своего первоначального направления. Качественные зависимости эффективного сечения рассеяния для атомов различных газов даны на рис. 2.

Наличие «провала» в зависимости объясняется следующим образом. Поскольку атом инертного газа представляет собой компактное образование (подоболочки атома заполнены), потенциал взаимодействия в грубом приближении можно заменить прямоугольной потенциальной ямой, как на рис. 1, вследствие чего и реализуется эффект Рамзауэра.

Рис. 2. Качественные зависимости эффективного сечения рассеяния электрона от энергии для ксенона (1) и кислорода (2)

Интенсивность пучка электронов при прохождении через газ в зависимости от глубины проникновенияизменяется по экспоненциальному закону

,

где – интенсивность первоначального пучка,– концентрация атомов газа. Отсюда следует, что при фиксированной глубине проникновенияпотока электронов его интенсивность увеличивается с уменьшением эффективного сечения, либо наоборот, убывает, если сечениеувеличивается. Данную связь можно использовать для определения минимумов и максимумов в зависимости, поскольку интенсивность потока нерассеянных электронов сравнительно легко определяется в эксперименте.

С помощью выражения (5) можно оценить размеры потенциальной ямы атома и определить его радиус по формуле:

. (6)

Добавление слагаемого в формуле (6) связано с тем, что потенциальную энергию электрона вдали от атома следует считать нулевой, тогда в области атома она будет отрицательной. Это соответствует смещению всего графикана рис. 1. вниз на величину, вследствие чего энергия электрона в областиII увеличивается на это же значение.