24.Периодическая система элементов д.И. Менделеева.

Наиболее распространёнными являются 3 формы таблицы Менделеева: «короткая» (короткопериодная), «длинная» (длиннопериодная) и «сверхдлинная». В «сверхдлинном» варианте каждый период занимает ровно одну строчку. В «длинном» варианте лантаноиды и актиноиды вынесены из общей таблицы, делая её более компактной. В «короткой» форме записи, в дополнение к этому, четвёртый и последующие периоды занимают по 2 строчки; символы элементов главных и побочных подгрупп выравниваются относительно разных краёв клеток. Помимо перечисленных выше, периодическому закону соответствуют и некоторые другие характеристики элементов:

Электронная конфигурация. Организация электронов демонстрирует определенный повторяющийся периодический образец. Электроны занимают последовательность оболочек, которые идентифицируются числами (оболочка 1, оболочка 2 и т. д.), а те, в свою очередь, состоят из подуровней, определяемых литерами s, p, d, f и g. По мере увеличения атомного числа электроны постепенно заполняют эти оболочки; каждый раз, когда электрон впервые занимает новую оболочку, начинается новый период в таблице. Сходства в электронной конфигурации обусловливают подобие свойств элементов (наблюдение за которыми, собственно, и привело к открытию периодического закона).

Металличность / неметалличность. По мере снижения показателей энергии ионизации, электроотрицательности и энергии сродства к электрону элементы приобретают черты, характерные для металлов, а по мере их возрастания — напротив, для неметаллов. В соответствии с закономерностями для упомянутых характеристик, наиболее ярко выраженные металлы располагаются в начале периода, а неметаллы — в его конце. В группах, напротив, по мере движения сверху вниз металлические свойства усиливаются, хотя и с некоторыми исключениями из общего правила. Сочетание горизонтальных и вертикальных закономерностей придает условной разделительной линии между металлами и неметаллами ступенчатый вид; расположенные вдоль этой линии элементы иногда определяются как металлоиды

25) Законы геометрической оптики.

1. Закон прямолинейного распространения света : в прозрачной однородной среде свет распространяется по прямым линиям.

В связи с законом прямолинейного распространения света появилось понятие световой луч, которое имеет геометрический смысл как линия, вдоль которой распространяется свет. Реальный физический смысл имеют световые пучки конечной ширины. Световой луч можно рассматривать как ось светового пучка.Поскольку свет, как и всякое излучение, переносит энергию, то можно говорить, что световой луч указывает направление переноса энергии световым пучком. Также закон прямолинейного распространения света позволяет объяснить, как возникают солнечные и лунные затмения.

2. Закон независимого распространения лучей — второй закон геометрической оптики, который утверждает, что световые лучи распространяются независимо друг от друга. Так, например, при установке непрозрачного экрана на пути пучка световых лучей экранируется (исключается) из состава пучка некоторая его часть. Однако, по свойству независимости необходимо считать, что действие лучей оставшихся незаэкранированными от этого не изменится.

То есть предполагается, что лучи не влияют друг на друга, и распространяются так, как будто других лучей, кроме рассматриваемого, не существует.

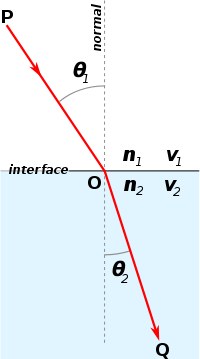
3. Закон отражения света — устанавливает изменение направления хода светового луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части. Широко распространённая, но менее точная формулировка «угол отражения равен углу падения» не указывает точное направление отражения луча. Тем не менее, выглядит это следующим образом:

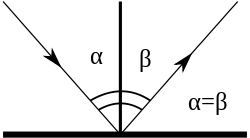
4. Закон Снеллиуса (также Снелля или Снелла) описывает преломление света на границе двух прозрачных сред. Также применим и для описания преломления волн другой природы, например звуковых.

• Теоретическое объяснение закона Снеллиуса — см. в статье Преломление.

Закон был открыт в начале XVII века голландским математиком Виллебрордом Снеллиусом^[1]. Несколько позднее опубликован (и, возможно, независимо переоткрыт) Рене Декартом.

Угол падения света на поверхность связан с углом преломления соотношением

Здесь:

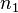• — показатель преломления среды, из которой свет падает на границу раздела;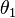

• — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности;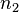

• — показатель преломления среды, в которую свет попадает, пройдя границу раздела;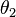

• — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности.

5. Закон обратимости светового луча. Согласно ему, луч света, распространившийся по определённой траектории в одном направлении, повторит свой ход в точности при распространении и в обратном направлении.

Поскольку геометрическая оптика не учитывает волновой природы света, в ней действует постулат, согласно которому если в какой-то точке сходятся две (или большее количество) систем лучей, то освещённости, создаваемые ими, складываются.

26

Электромагнитное излучение принято делить по частотным диапазонам (см. таблицу). Между диапазонами нет резких переходов, они иногда перекрываются, а границы между ними условны. Поскольку скорость распространения излучения (в вакууме) постоянна, то частота его колебаний жёстко связана с длиной волны в вакууме.

Название диапазона		Длины волн, λ	Частоты, ν	Источники
Радиоволны	Сверхдлинные	более 10 км	менее 30 кГц	Атмосферные имагнитосферныеявления. Радиосвязь.
	Длинные	10 км — 1 км	30 кГц — 300 кГц
	Средние	1 км — 100 м	300 кГц — 3 МГц
	Короткие	100 м — 10 м	3 МГц — 30 МГц
	Ультракороткие	10 м — 1 мм	30 МГц — 300 ГГц[4]
Инфракрасное излучение		1 мм — 780 нм	300 ГГц — 429 ТГц	Излучение молекул и атомов при тепловых и электрических воздействиях.
Видимое (оптическое) излучение		780—380 нм	429 ТГц — 750 ТГц
Ультрафиолетовое		380 — 10 нм	7,5·1014 Гц — 3·1016 Гц	Излучение атомов под воздействием ускоренных электронов.
Рентгеновские		10 нм — 5 пм	3·1016 — 6·1019 Гц	Атомные процессы при воздействии ускоренных заряженных частиц.
Гамма		менее 5 пм	более 6·1019 Гц	Ядерные и космические процессы, радиоактивный распад.

27)

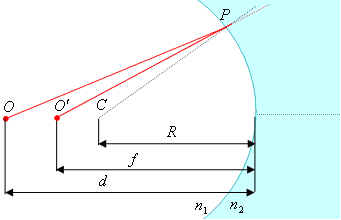
Преломление на сферической поверхности. Когда луч падает на сферическую границу раздела двух сред, построение отраженного и преломленного лучей производится следующим образом: строится плоскость касания в точке падения луча на сферическую поверхность и восстанавливается нормаль к этой плоскости в точке падения (рис. 6.25). Далее преломленный луч проводится в соответствии с законом преломления.

Рассмотрим преломление лучей на сферической поверхности прозрачной среды, такой, например, как одна из поверхностей линзы. Предположим, что источник света Онаходится в среде с показателем преломления , и лучи, исходящие из него, попадают в среду с показателем преломления (рис. 6.26). Пусть R – радиус кривизны сферической границы раздела этих сред, С – центр сферы. Покажем, что все лучи, выходящие из точки О, соберутся в одной точке , являющейся изображением точки О, если ограничиться лучами, составляющими малый угол с осью и друг с другом. Такие лучи называются параксиальными. Геометрическая оптика – наука неточная, и одно из важнейших ее упрощений – приближение параксиальной оптики. Суть его заключается в том, что рассматриваются только те лучи, которые на своем пути незначительно отклоняются от оптической оси системы. Тогда угол между оптической осью и падающим лучом настолько мал, что можно считать, что .

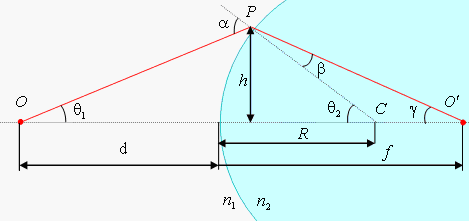
Рис. 6.26

Рассмотрим один из лучей, выходящих из точки О. Луч преломится в точке Р на границе раздела двух сред, согласно закону преломления:

.

Поскольку мы рассматриваем параксиальные лучи, то закон преломления можно записать следующим образом:

.

Из рис. 6.26 видно, что , следовательно,

.

(6.3)

Вследствие малости углов можно считать, что , , . Подставляя значения углов в (6.3) и поделив все члены на h, получим

.

(6.4)

Рис.6.27

Из (6.4) видно, что при заданном расстоянии d от сферической поверхности до источника расстояние от сферической поверхности до изображения f не зависит от угла, который луч образует с осью. Следовательно, все параксиальные лучи сходятся в одной точке .

На рис. 6.26 лучи падают на выпуклую часть сферической поверхности. Но полученное соотношение (6.4) справедливо и для вогнутой поверхности. Это видно из рис. 6.27, если считать, что R и f являются отрицательными. Заметим, что в случае вогнутой поверхности изображение получается мнимым.

Линзы

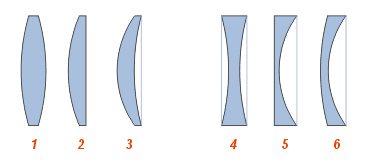Виды линз: Собирающие:  1 — двояковыпуклая  2 — плоско-выпуклая  3 — вогнуто-выпуклая (положительный(выпуклый) мениск) Рассеивающие:  4 — двояковогнутая  5 — плоско-вогнутая  6 — выпукло-вогнутая (отрицательный(вогнутый) мениск)

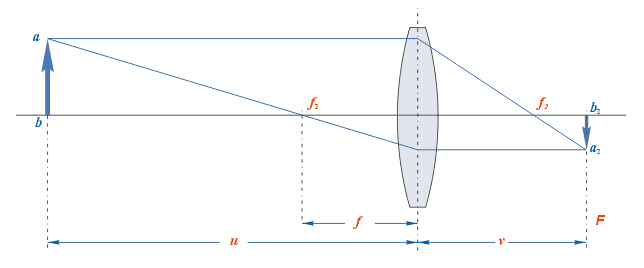
Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы (открытой Исааком Барроу):

где  — расстояние от линзы до предмета;  — расстояние от линзы до изображения;  — главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей.

28)