4.4.3 Законы распределения случайной величины, применяемые в технологии машиностроения

Распределение случайных величин в зависимости от условий могут подчиняться вполне определенным законам: Гаусса, равной вероятности, Симпсона. Наибольшее практическое значение в технологии машиностроения имеет дифференциальная функция закона нормального распределения (закон Гаусса), для которого плотность вероятности или дифференциальная функция распределения:

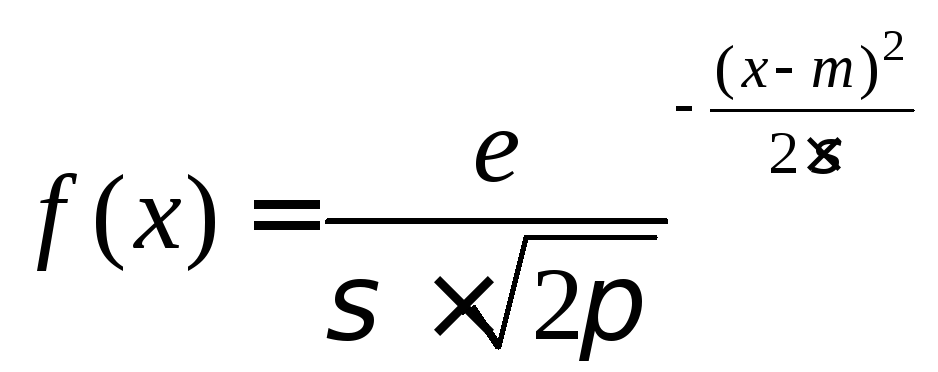
где x – переменная случайная величина;

σ– среднее квадратичное отклонениеxотm;

m– математическое ожидание величиныx.

Дифференциальная функция закона нормального распределения графически изображается холмообразной кривой, симметричной относительно центра группирования (рис. 4.5).

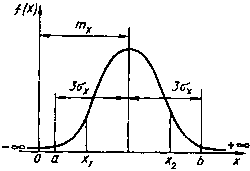
Рисунок 4.5 – Дифференциальный закон нормального распределения случайной величины

Координата центра группирования определяет положение кривой относительно начала отсчета, а параметр σ(среднее квадратичное отклонение) – ее форму и размах.

Закон равной вероятности встречается, когда наряду со случайными факторами, вызывающими рассеяние, действует доминирующий систематический фактор непрерывно или равномерно изменяющий во времени положение центра группирования m. Графически такое распределение случайной величины отображается прямоугольником (рис. 4.6).

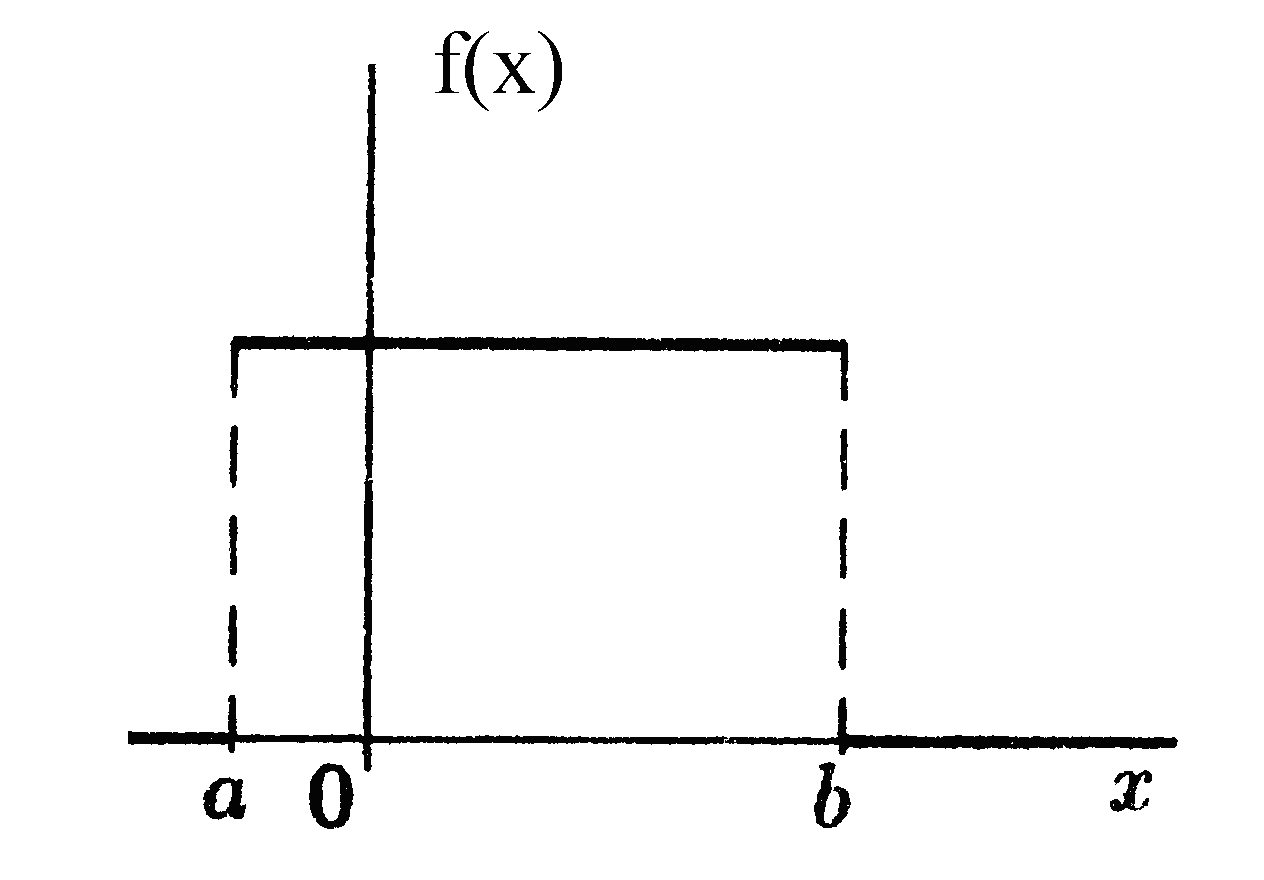
Рисунок 4.6 – Распределение случайной величины по закону равной вероятности

 

Дифференциальная функция распределения закона равной вероятности:

.

К распределению по закону Симпсона (закон треугольника) приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Графически кривая рассеяния имеет вид равностороннего треугольника (рис. 4.7).

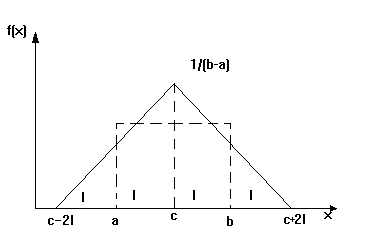
Рисунок 4.7 – Распределение случайной величины по закону Симпсона

Дифференциальная функция распределения закона Симпсона:

при

при

при

4.4.4 Выбор закона распределения

Во многих практических задачах точный закон распределения неизвестен. Поэтому выдвигается гипотеза о соответствии имеющегося эмпирического закона, построенного по наблюдениям, некоторому теоретическому. Данная гипотеза требует статистической проверки, по результатам которой будет либо подтверждена, либо опровергнута.

Пусть X– исследуемая случайная величина. Требуется проверить гипотезуH₀о том, что данная случайная величина подчиняется закону распределенияF(x). Для сравнения эмпирического и гипотетического законов используется правило, называемое критерием согласия.

Одним из популярных является критерий согласия хи-квадрат К. Пирсона.

В нем вычисляется статистика хи-квадрат:

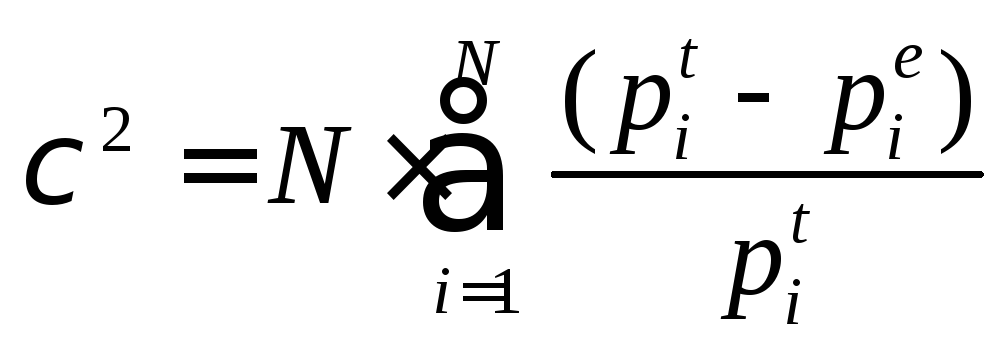
где N– число интервалов, по которому строился эмпирический закон распределения (число столбцов соответствующей гистограммы),

i– номер интервала,

– вероятность попадания значения случайной величины вi-й интервал для теоретического закона распределения,

– вероятность попадания значения случайной величины в i-й интервал для эмпирического закона распределения.

Для ответа на вопрос о принятии нулевой гипотезы необходимо найти теоретическое значение критерия – критическую точку хи²_теор. Его выбирают по "Таблице критических точек хи²" в зависимости от принятого уровня значимостиa(0,05; 0,01; 0,005; 0,001) и числу степеней свободыk=s-1-r, гдеs– число интервалов,r– количество параметров предполагаемого распределения (для нормального законаr= 2, тогдаk=s–3).

Далее сравнивают наблюдаемое значение критерия с теоретическим: если наблюдаемое значение критерия меньше теоретического, то нулевую гипотезу принимают, в противном случае – отвергают.