
Синтез КЛС
.pdfВведение
Во все времена люди стремились совершенствовать вычислительные стройства, переданные им предыд щими по олениями.
История вычислительной техни и рас р чивается а |
снежный пото |
и впереди новые оризонты для лавины от рытий. |
Механичес ая |
вычислительная машина Чарльза Бэббиджа се одня воспринимается а фантасти а, а омпьютер превратился в персональн ю принадлежность, постепенно обретая все новые черты своих создателей.
Зададим себе вопрос: «Что должен знать изобретатель ЭВМ»? Се одня мы знаем, что создатель первой действ ющей ЭВМ –
Джон Винсент Атанасов в онце 30-х одов применил ал ебр двоичных чисел и спрое тировал простейшие элементы схемы на эле тронных лампах. С тех пор стремительная модернизация аппаратных средств была бы невозможна без развития на и о синтезе цифровых стройств вычислительной техни и.
Специалист в области информати и и вычислительной техни и должен свободно ориентироваться в архите т ре омпьютера, иметь пра - ти разработ и простейших базовых стройств (с мматоров, преоб-
разователей |
одов, ло ичес их омм таторов, пол автоматов) и на их |
основе стр |
т рировать бло и простейших ЭВМ. |
Прое тирование цифровых стройств – это про раммирование на |
|
физичес ом |
ровне. Язы ом описания цифровых стройств является |
б лева ал ебра. Техноло ия про раммирования на физичес ом ровне в лючает: постанов техничес о о задания и е о формализацию; минимизацию б левой ф н ции (системы равнений); представление принципиальной схемы в различных элементных базисах; сбор и провер работоспособности схемы. Ка этом на чить? Оптимальное решение – это создать чебно-методичес ий омпле с, состоящий из аппаратных, про раммных и методичес их средств.
В ачестве аппаратных средств, в данном сл чае, использ ется ниверсальный цифровой стенд «УЦС-1», разработанный в 1990 од на афедре информати и и вычислительной техни и ниверситета. Для демонстрации применяется стенд «ОА и ВТ» – разработ а Омс о о
ос дарственно о педа о ичес о о |
ниверситета. К аппаратным |
|
средствам та же отнесем омпьютеры и сетевое обор дование. |
||
Про раммные средства, позволяющие эм лировать цифровые с- |
||
тройства и ос ществлять вирт альн ю провер |
их работы: VHDL, |
|
Electronic Workbench Multisim v6.0 и др |
ие. |
|
Методичес ая поддерж а – настоящий пра ти |
м, чебные сред- |
|
ства на даленном сервере, чебный пра ти м на CD – дис е, основная и дополнительная литерат ра, в лючая периодичес ие издания и, онечно, рс ле ций.
3
Принцип работы с |
ниверсальным |
|
|||
цифровым стендом «УЦС-1» |
|
||||
Универсальный стенд «УЦС-1» представляет собой цифровое эле - |
|||||
тронное стройство, на переднюю омм тационн ю панель выведены |
|||||
онта ты цифровых ми росхем. На панели имеются рафичес ие изоб- |
|||||
ражения ло ичес их элементов, оторые содержатся в ми росхемах. |
|||||
Эти изображения по азывают, что все элементы являются ф н цио- |
|||||
нально полными и выполняют операцию онъюн ции с инверсией – |
|||||
«И-НЕ». |
|
|
|
|
|
Необходимо отметить, что все элементы являются ф н циональ- |
|||||
но независимыми др |
от др |
а и мо |
т использоваться в различных |
||
омбинациях. Все входные си налы подаются на левые (по схеме) |
он- |
||||
та ты, выходные ф н ции этих переменных находятся справа от |
ра- |
||||
фичес о о изображения. В наборе стенда имеются 4 типа ло ичес их |
|||||
элементов: |
|
|
|
|
|
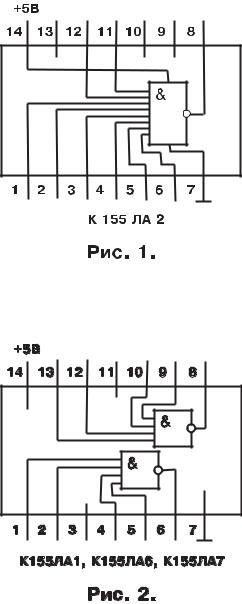
– 8 – входовой элемент, представ- |
|
|
|||
ляющий собой одн |
|
ми росхем |
|
|
|
К155ЛА2 (рис. 1); |
|
|
|
|
|
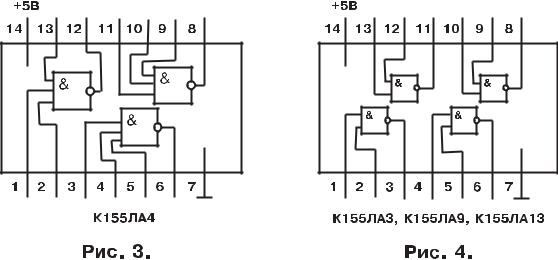
– 4 – входовой элемент (в одном |
|
|
|||
орп се ми росхемы содержится 2 |
|
|
|||
элемента) К155ЛА1 (рис. 2); |
|
|
|
||
– 3 – входовой элемент (в ми ро- |
|
|
|||
схеме 3 элемента) К155ЛА4 (рис. 3); |
|
|
|||
– 2 – входовой (в ми росхеме – 4 |
|
|
|||
элемента) К155ЛА3 (рис. 4). |
|
|
|
||
Каждый вход элементов имеет два |
|
|
|||
онта та, необходимых для размноже- |
|
|
|||
ния эле тричес их связей в том сл чае, если один выход ло ичес о о |
|||||
элемента под лючается |
нес оль им входам др их ло ичес их эле- |
||||
ментов. Ор анизация эле тричес их |
|
|
|||
связей ос ществляется с помощью |
|
|
|||
омм тационных шн ров. |
|
|
|
||
С левой стороны стенда располо- |
|
|
|||
жены 4 т мблера, связанные с |
|
|
|||
инди аторами – это |
енераторы «н - |
|
|
||
лей» и «единиц», необходимые для |
|
|
|||
то о, чтобы реализовать любые зна- |
|
|
|||
чения входных переменных. |
|
|
|
||
Если т мблер находиться в верх- |
|
|
|||
нем (по схеме) положении, |
то орит |
|
|
||
светодиод, на выходной |
лемме |
|
|
||
4 |
|
|
|
|
|
данно о енератора прис тств ет ровень ло ичес ой «1». Если т мблер находиться в нижнем (по схеме) положении, то светодиод не о-
рит, а на выходной лемме данно о |
енератора прис тств ет |
ровень |
ло ичес о о «0». На нижней лемме |
енератора – инверсный |
си нал. |
С правой стороны стенда расположены 4 выходных леммы, связанных с инди аторами - они предназначены для определения значения выходной пере лючательной ф н ции, синтезир емой ло ичес ой схемы. Выходной си нал схемы под лючается любой из 4-х лемм. Если ф н ция равна «1», то светодиод орит, если же ф н ция равна «0», то инди ация отс тств ет.
Необходимо отметить особенность ми росхем серии К155, на о- торых собран данный стенд. Если входы ло ичес их элементов этих ми росхем не задействованы (т.е. «висят»), то элементами на данных входах воспринимается ровень ло ичес ой единицы – «1».
Если надо использовать элемент в ачестве инвертора (операция «НЕ»), достаточно на один из входов подать цифровой си нал, то да на выходе ло ичес о о элемента пол чим инверсное значение (остальные входы не задействованы).
Стенд «УЦС-1» в лючается в сеть 220 В с помощью мало абаритно о бло а питания на 5В/200 мА. На омм тационных леммах напряжения 0 и 5В.
5

Теоретичес ая часть
1. Ал ебра ло и и – математичес ая основа цифровой автомати и
Напомним, что б лева ал ебра, иначе ал ебра ло и и, основана на базе двоичной системы счисления, и все рез льтаты ал ебраичесих преобразований и вычислений, в онечном ито е, сводятся ис-
тинном «1» или |
ложном «0» выс азыванию. В б левой ал ебре |
использ ется толь о три ло ичес ие операции. |
|
Операция «И» |
( онъюн ция) выполняет ло ичес ое множение |
входных переменных. Предположим, что имеются две переменные А и В, оторые мо т принимать значения «0» (ложное) и «1» (истинное), то да онъюн ция этих переменных Y=A&B тоже может принимать значения «0» или «1» при определенных омбинациях этих входных переменных. Полная запись этих омбинаций составляет таблиц истинности выходной (пере лючательной) ф н ции Y:
A |
B |
|
|
Y |
Y = 0 & 0 = 0 |
0 |
0 |
|
|
0 |
Y = 0 & 1 = 0 |
0 |
1 |
|
|
0 |
|
|
Y = 1 & 0 = 0 |
||||
1 |
0 |
|
|
0 |
|
|
Y = 1 & 1 = 1 |
||||
1 |
1 |
|
1 |
||
Табличное описание сл жит добным формализованным язы ом взаимопонимания межд разработчи ом и за азчи ом.
Операция «ИЛИ» (дизъюн ция) выполняет ло ичес ое сложение входных переменных A и B то их дизъюн ция Y=A V B имеет след ю- щ ю таблиц истинности:
A |
B |
|
Y |
Y = 0 V 0 = 0 |
0 |
0 |
|
0 |
Y = 0 V 1 = 1 |
0 |
1 |
|
1 |
|
|
Y = 1 V 0 = 1 |
|||
1 |
0 |
|
1 |
|
|
Y = 1 V 1 = 1 |
|||
1 |
1 |
|
1 |
Операция «НЕ» (инверсия) выполняет ло ичес ое отрицание. Операция пред сматривает изменение значения переменной или ф н - ции на противоположное. Пере лючательная ф н ция Y имеет след - ющ ю таблиц истинности:
A Y |
Y = 0 = 1 |
|
01
10 Y = 1 = 0
6
С помощью этих трех ло ичес их операций можно задавать с оль одно сложные выходные (пере лючательные) ф н ции, имеющие неораниченное оличество входных переменных. Для то о, чтобы можно было оворить о значении ф н ции при определенной омбинации входных переменных, необходимо иметь либо ал ебраичес ое описание этой ф н ции, либо ее таблиц истинности. При наличии равнения выходной ф н ции из таблицы истинности можно записать б лево равнение. Все о с ществ ет три инвариантных способа формализации цифровых стройств:
а) таблица истинности или ее рафичес ая арта; б) б лево равнение;
в) эпюры – осцилло раммы входных и выходных си налов.
Для то о, чтобы можно было совершать ал ебраичес ие преобразования над заданным равнением, использ ются за оны и а сиоы б левой ал ебры.
Закон двойного отрицания
=
Y = A = A
Закон де Моргана
Y = A V B = A & B;
Y = A & B = A V B.
Закон поглощения
Y = A V A = A;
Y = A V A & B = A V B;
Y = A & A = A.
7

Операции с константами
Y = A V 1 = 1;
Y = A V 0 = A;
Y = A & 1 = A;
Y = A & 0 = 0.
Операции с инверсными значениями
Y = A & A = 0;
Y = A V A = 1.
2. Ло ичес ие элементы пере лючательных ф н ций
Современной промышленностью вып с аются цифровые ми росхемы, реализ ющие всевозможные пере лючательные ф н ции. Ка им же образом перейти от равнений их техничес ой реализации? Мы не б дем рассматривать вн тренние схемы ло ичес их элементов, та а это очень большой раздел из области эле трони и, разберем толь о работ ф н ционально–за онченных бло ов (элементов).
В эле трони е ло ичес ий ноль «0» реализ ется подачей на соответств ющий вход напряжения, ровень оторо о близо н левом потенциал , а ло ичес ая «1» – подачей напряжения, ровень оторо- о близо напряжению источни а питания самой ми росхемы.
Ка ие же бывают ло ичес ие элементы?
 U
U
U » Un
“1” |
|
|
|
|
||
|
|
|
|
|||
|
|
“0” |
“1” |
“0” |
||
“0” |
|
|
|
|
t |
|
|
|
|
|
|||
|
|
|
|
|||
U » 0 |
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
8
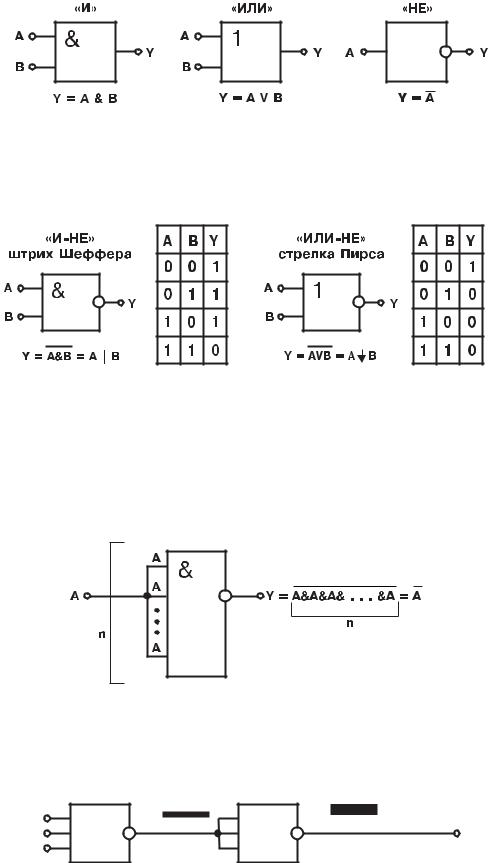
Вот представлено рафичес ое изображение ло ичес их элементов, выполняющих элементарные ф н ции «И», «ИЛИ», «НЕ».
С ществ ют и др ие ло ичес ие элементы, оторые реализ ют более сложные ф н ции, та ие, а «И-НЕ», «ИЛИ-НЕ», «ИСКЛЮЧАЮЩЕЕ ИЛИ» и др ие.
Необходимо отметить, что элементы «И-НЕ» и «ИЛИ-НЕ» обладают ф н циональной полнотой, то есть любое равнение пере лючательной ф н ции можно реализовать либо на элементах «И-НЕ», либо на «ИЛИ-НЕ». До ажем это.
Для создания на основе «И-НЕ» элемента, выполняюще о операцию «НЕ», необходимо соединить все е о входы:
В соответствии с за оном по лощения пол чаем: A•A•A•...•А=А. Для выполнения операции «И» необходимо инвертировать выход-
н ю ф н цию:
A |
& |
Y = A&B&C |
& |
Y = A&B&C = A&B&C |
|
|
|||
B |
|
|
|
Y |
C |
|
|
|
|
9
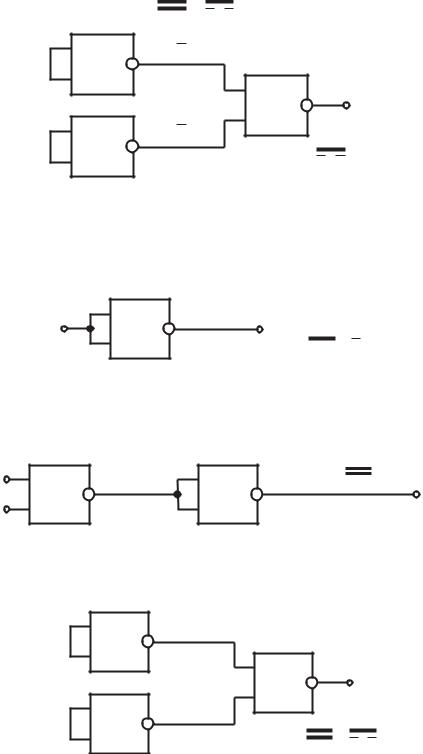
Для реализации элемента «ИЛИ» надо воспользоваться за оном де Мор ана:
Y = AVB = AVB = A&B
A
B 
&
&
A
&
Y
B
Y = A&B = AVB
Анало ично реализ ются все операции на элементе «ИЛИ-НЕ».
Операция инверсии
A |
1 |
Y |
|
|
Y = AVA = A |
A
B
|
Операция дизъюн ции |
|
1 |
1 |
Y = AVB = AVB |
|
|
|
|
|
Y |
Операция онъюн ции
A
B
1 |
1 |
1 |
Y |
|
Y = A&B = A&B = AVB
10

3. Анализ и синтез омбинационных ло ичес их схем
Комбинационная ло ичес ая схема (КЛС) – это схема эле тричесих соединений ло ичес их элементов, реализ ющая определенн ю ф н цию, описываем ю заданным ал ебраичес им равнением, таблицей истинности или эпюрой (осцилло раммой си налов на входе и выходе).
Люб ю КЛС можно представить в виде «черно о ящи а», имеюще о n–входных переменных и m–выходных ф н ций.
X1 |
Y1 |
X2 |
Y2 |
|
Z |
Xn |
Ym |
Y1 = f1 (X1, X2, …, Xn) Y2 = f2 (X1, X2, …,Xn)
-- - - - - - - - - - -
-- - - - - - - - - - -
-- - - - - - - - - - -
Ym = fm (X1, X2, …, Xn)
Данная система равнений полностью описывает состояние всех пере лючательных ф н ций КЛС. Реализация аждой из этих ф н ций
– этап синтеза «черно о ящи а».
Лабораторные работы пра ти ма ориентированы на применение след юще о ал оритма действий:
1.Форм лиров а техничес о о задания (Т3);
2.Представление словесно о портрета ТЗ и бло -схемы стройства;
3.Составление таблицы истинности и переход ( а правило)
рафичес ой форме – арте Карно; 4. Запись минимизированно о равнения;
5.Синтез схемы в базисе элементов Шеффера;
6.Сбор а схемы на стенде, провер а работоспособности.
7.Компьютерное моделирование и защита прое та.
Для минимизации ф н ции использ ется ал ебраичес ий или ра-
фичес ий метод. След ет отметить, что рафичес ий метод – пред- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ставление таблиц истинности ар- |
|
|
A |
B |
C |
|
|
Y |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тами Карно позволяет значитель- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
0 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но |
с орить расчет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В ачестве примера предста- |
|
|
0 |
1 |
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вим |
арт Карно для таблицы со- |
|||||
|
1 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стояний трехвходовой ф н ции |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
1 |
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 1.). |
|||||
|
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11

Запишем по этой таблице равнение для выходной ф н ции Y в дизъюн тивной нормальной форме (ДНФ):
Y = A & B & C V A & B & C V A & B & C V A & B & C V A & B & C
Использ ем арт Карно для минимизации ф н ции.
Графи а арты Карно основана на за онах симметрии, а по лощение (A V A = 1) на операции с инверсными значениями для входных переменных. Необходимо объединить в р ппы лет и, в о- торых Y = 1 (минтермы). При объединении минтермов в р ппы необходимо р оводствоваться след ющими правилами.
1.Гр ппа должна представлять:
а) вадрат ма симальной величины; симметричные вадраты;
б) стро , столбец; симметричные стро и, столбцы; в) термы, симметричные относительно оси симметрии
( р ппа W, рис. 2.);
) соседние термы – по верти али, оризонтали
( р ппа Z, рис.2.).
группа Z |
|
|
|
|
|
A |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
группа T |
||
|
|
|
|
0 |
|
|
|
1 |
|
|
1 |
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C |
|
1 |
|
|
|
0 |
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
группа W |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 2. |
|
|
|
|
|||||||
2. Количество р пп должно быть минимально, одна о лет -терм можно использовать неодно ратно в разных р ппах.
3.Произведение неизменяющихся вн три р ппы входных переменных образ ет ис омый минтерм.
4.С мма минтермов р пп представляет собой ис ом ю минимизированн ю ф н цию.
Представим объединение в р ппы на рис н е 2. Запишем выражения для р пп:
Z = B & C; |
T = A & B; |
W = C & B. |
Запишем ис омое минимизированное б лево выражение:
Y = Z V T V W = B&C V A&B V C&B.
Упражнение. Синтезир йте по данном равнению омбинационн ю схем на базе элементов «И-НЕ».
12
