2. Объём прямого цилиндрического тела.

Пусть F– плоская фигура. Восставим в каждой точке этой фигуры перпендикуляр к содержащей её плоскости и отложим на каждом перпендикуляре отрезок длиныh(все отрезки располагаются по одну сторону от плоскости). Множество точек этих отрезков образует телоL, которое называется прямым цилиндрическим телом с основаниеFи высотойh. Вторые концы построенных отрезков образуют фигуруF', конгруэнтную основаниюFи параллельные ему.

В случае, когда F– прямоугольник, прямое цилиндрическое тело является прямоугольным параллелепипедом. Если жеF– ступенчатая фигура, тоL– ступенчатое тело, причём оно разлагается на прямоугольные параллелепипеды, имеющие одинаковые высоты. Объём этого ступенчатого тела равен произведению площади фигурыFна высоту тела:

(1) V(L)=S(F)h.

Докажем, что формула (1) остаётся справедливой и в более общем случае. Именно, справедливо следующее утверждение:

Теорема 1:Если плоская фигура А квадрируема, то прямое цилиндрическое телоLс основание А кубируемо, причём его объём равен произведению площади фигуры А на высоту тела:

V(L) =S(А)h.

Доказательство:

Не теряя общности, мы можем считать, что плоскость фигуры А является координатной плоскостью Оху. Так как по условию фигура А квадрируема, то для любого > 0 найдутся ступенчатые фигурыF₁ иF₂такие, чтоF₁ АF₂, причёмS(F₂) –S(F₁) <.

Построим ступенчатые тела L₁иL₂с высотойhи основаниямиF₁ иF₂. Тогда имеем:

L₁LL₂.

При этом

V (L₂) - V (L₁) = S (F₂) h – S (F₁) h = h ( S (F₂) – S (F₁) ) < h = .

Таким образом, для любого> 0 найдутся ступенчатые телаL₁иL₂ такие, что

L₁LL₂иV(L₂) –V(L₁) <.

Поэтому тело Lкубируемо. При этом, как мы видели,

S(F₁)h<V(L) <S(F₂)h.

С другой стороны, из неравенств S(F₁) <S(А) <S(F₂) вытекает, что

S(F₁) h <S(А)h <S(F₂) h.

Мы видим, что числа V(L) иS(А)hразделяют одни и те же множества, а именно

{ S (F₁) h } и { S (F₂) h },

где, напомним, F₁– ступенчатые фигуры, содержащиеся в А, аF₂– ступенчатые фигуры, содержащие А. Но эти два множества, в силу квадрируемости А, разделяются лишь одним числом. Поэтому

V(L) =S(А)h.

Формула (1) доказана для любых квадрируемых фигур А.

3. Вычисление объёма тела по площадям параллельных сечений.

В этом пункте мы выведем основную формулу, позволяющую выразить объём тела через площади сечений этого тела, параллельных некоторой плоскости.

Определение. Тело Т назовём регулярным, если существует такая плоскость П, что

а) тело Т лежит по одну сторону от этой плоскости;

б) все сечения тела Т плоскостями, параллельными плоскости П, квадрируемы;

в) площадь S(x) сеченияQ(x), параллельного плоскости П и отстоящего от неё на расстояние х, является непрерывной функцией от х;

г) если S(х₁) иS(х₂), то проекция сеченияQ(x₂) на плоскость П содержит проекцию сеченияQ(x₁) на ту же плоскость.

Теорема 2. Если тело Т регулярно, то оно кубируемо, причём его объём выражается формулой

(2) V (T) = S (x) dx.

Здесь S(x) – площадь сечения тела т плоскостью, параллельной плоскости П и отстоящей от неё на расстояние х,а– наименьшее из расстояний точек тела Т от плоскости П,в– наибольшее из этих расстояний (см. рис. 42, гдеа= 0).

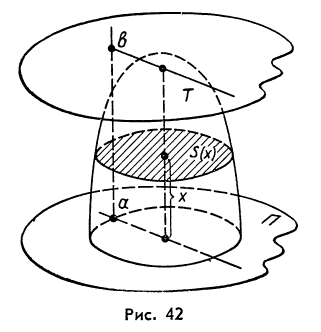
Доказательство. Рассмотрим некоторое разбиение отрезка [а; в]:

а=х₀ <х₁<х₂ < … <х_n< = b и на расстоянияхх₀,х₁,х₂ , … ,х_nпроведём плоскости, параллельные плоскости П. Данное тело Т этими плоскостями разобьётся на частичные «ломтики» Т₀, Т₁, …, Т_n-1.

Рассмотрим к-ый частичный «ломтик». Его высота равнах_к = х_к+1 – х_к. Так как функция у =S(x) непрерывна на [х_к; х_к+1], то она принимает на этом отрезке наибольшее и наименьшее значения. Наименьшее значение площади сечения для этого «ломтика» обозначимs_киS_к. В силу условия г) регулярности тела Т цилиндрическое тело с основаниемs_к лежит внутри частичного «ломтика», а цилиндрическое тело с основаниемS_кцеликом его содержит. ОбъёмV_квнутреннего цилиндрического тела будет

V_к =s_к х_к.

Объём V_к внешнего цилиндрического тела будет

V_к =S_к х_к.

Объединяя все внутренние и все внешние цилиндрические тела, получим два тела L₁иL₂такие, чтоL₁LL₂ . Объём телаL₁будет равен

s_к х_к,

а объём тела L₂ равен

S_к х_к.

Но s_к х_киS_к х_кявляются нижней и верхней суммами Дарбу для интегралаS(x)dx. Поэтому для любого> 0 найдётся такое разбиение отрезка [а; в], что

S_к х_к– s_к х_к <,

т.е.

V(L₂) -V(L₁) <.

Отсюда следует, что тело Т кубируемо. При этом объём тела V(T) удовлетворяет неравенствам

s_к х_кV(T)S_к х_к.

Но с другой стороны,

s_к х_к S (x) dx S_к х_к.

Значит, числа V(T) иS(x)dx разделяют одни и те же числовые множества

{s_к х_к} и {S_к х_к}.

Поскольку эти множества разделяются лишь одним числом, то V(T) =S(x)dx, что и требовалось доказать.

Пример 1. Вычислить объём пирамиды, площадь основания которой равнаS, а высотаH(рис.43).

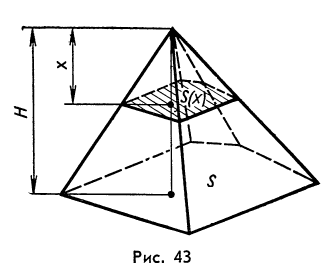
Решение. Так как , тоS(x) =

Следовательно,

V =

Пример 2.Вычислим объём шарового слоя, отсеченного от шарах²+у²+z²= 9 плоскостямих= 1 их= 2.

Решение.

Плоскость, перпендикулярная к оси абсцисс в точке х, пересекает шар по кругу радиусаr=. Площадь сеченияS(х) =r²=( 9 -х² )

и, следовательно

V=( 9 -х² )dx =(9х–)= 6.

4. Принцип Кавальери. Из формулы (2) п.3 вытекает следующее утверждение, называемое принципом Кавальери.

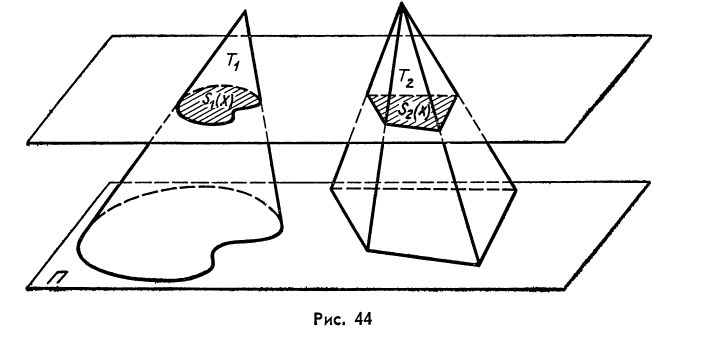Два кубируемых тела Т₁и Т₂(рис.44), ограниченные параллельными плоскостями, имеют равнее объёмы, если плоские сечения, параллельные указанным плоскостям и проведённые на одинаковых расстояниях от оснований, имеют равные площади.

Доказательство. Обозначим через V₁ объём тела Т₁, а черезV₂ – объём тела Т₂. Так как тела Т₁и Т₂кубируемы, то

V₁ (T₁) = S₁ (x) dx, V₂ (T₂) = S₂ (x) dx.

По условию, S₁(x) =S₂(x), значит, иV_{1 =} V₂.

Пример 3. Покажем, что объём полушара радиусаRравен разности объёмов цилиндра, радиус основания и высота которого равныR, и конуса с радиусом основанияR(рис.45).

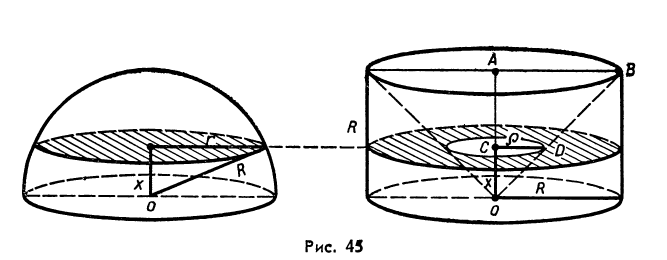Рассмотрим полушар. Обозначим черезS₁(x) площадь сечения, параллельного плоскости основания полушара, отстоящего от него на расстояниих. Учитывая, чтоr²=R²–х², найдёмS₁(х) =r²=(R²-х² ).

Обозначим через S₂(x) площадь сечения тела (цилиндр без конуса) плоскостью, параллельной основанию цилиндра и отстоящей от него на расстояниих :S₂(х) =R²-²=(R²-² ).

Из подобия треугольников ОАВ и ОСDимеем:=или=, откуда=х. Следовательно,S₂(х) =(R²-х² ), а потомуS₁(х) =S₂(х) и согласно принципу Кавальери объёмы рассматриваемых тел равны.

5. Объём тела вращения. Пусть Т – тело вращения, образованное вращение вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямымих = а, х = ви графиком непрерывной функцииу=f(x).

Докажем, что это тело вращения кубируемо и его объём выражается формулой

(3) V = f ²(x) dx = y ² dx.

Сначала докажем, что это тело вращения регулярно, если в качестве П выберем плоскость Оуz, перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстояниихот плоскости Оуz, является кругом радиусаf(x) и его площадьS(х) равнаf ²(x) (рис.46)

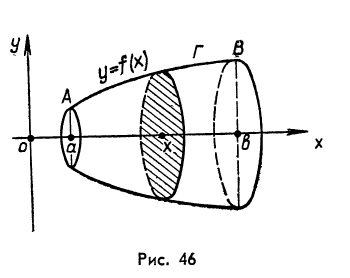
Поэтому функция S(х) непрерывна в силу непрерывностиf(x). Далее, еслиS(х₁)S(х₂), то значит, чтоf(х₁)f(х₂). Но проекциями сечений на плоскость Оуz являются круги радиусовf(х₁) иf(х₂) с центром О, и изf(х₁)f(х₂). Вытекает, что круг радиусаf(х₁) содержится в круге радиусаf(х₂).

Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объём вычисляется по формуле

V=S₁(x)dx= f ²(x)dx.

Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми у₁=f(x₁) иу₂=f(x₂), то

V = y dx – y dx = [ (f ₂(x))² – (f ₁(x))²] dx.

Формулой (3) можно воспользоваться и для вычисления объёма тела вращения в случае и для вычисления объёма тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определённого интеграла.

В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.

Например, найдём объём тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдём объём, получаемый при вращении прямоугольника с высотой у_к, в основании которого лежит отрезок [х_к; х_к+1]. Этот объём равен разности объёмов двух прямых круговых цилиндров

V_k=y_k x–y_k x=y_{k (}x_k+1+x_k) (x_k+1–x_k).

Но теперь ясно, что искомый объём оценивается сверху и снизу следующим образом:

m_к x_k х_кVM_к x_k+1х_к.

Отсюда легко следует, что

(4) V= 2хуdх.

Пример 4. Найти объём шара радиуса R.

Решение. Не теряя общности, будем рассматривать круг радиуса Rс центром в начале координат. Этот круг, вращаясь вокруг оси Ох, образует шар.

Уравнение окружности имеет вид х²+у²=R, поэтомуу² =R-х². Учитывая симметрию круга относительно оси ординат, найдём сначала половину искомого объёма

V_ш= у² dх = (R–х²) dх = (R²x–)=(R³ –) =R³ .

Пример 5. вычислим объём конуса, высота которого hи радиус основанияr.

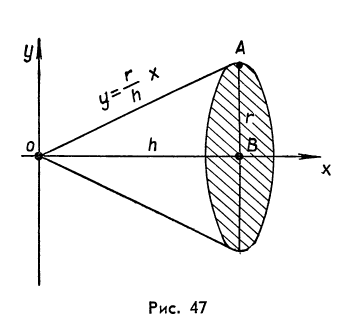
Решение. Выберем систему координат так, чтобы ось Ох совпала с высотойh(рис.47), а вершину конуса примем за начало координат. Тогда уравнение прямой ОА запишется в видеу=.

Пользуясь формулой (3), получим:

V=

Пример 6. Найдём объём тела, полученного при вращении вокруг оси абсцисс астроиды х=a cos³t,y=a sin³t. (рис.48).

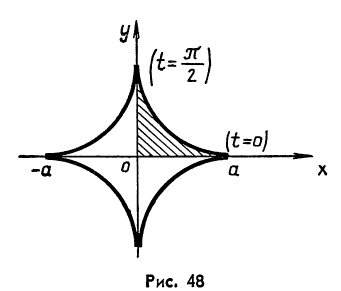
Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определённого интеграла, найдём для новой переменной tпределы интегрирования.

Если х = acos³t= 0, тоt=, а если х =a cos³t=а, тоt= 0.

Учитывая, что y² = a² sin⁶t, dx = - 3a cos²t sint dt,получаем:

V = у² dх = ( – 3a cos²t sint) a² sin⁶t dt = 3 a³ sin⁶t cos²t sint dt = 3 a³ ( sin⁷t dt – sin⁹t dt ).

Применяя реккурентную формулу, получаем, что

V=3a³ ( ) = 3a³(9 – 8) =3a³=a³.

Объём всего тела вращения будет a³.

Пример 7. Найдём объём тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды x = a (t – sint), y = a(1 – cost).

Решение. Воспользуемся формулой (4):

V= 2хуdх.

И заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной tот 0 до 2. Таким образом,

V = 2 a (t – sint) a (1– cost) a (1– cost) dt = 2 a³ (t – sint) (1– cost)²dt = 2 a³ ( t – sint – 2t cost + 2sint cost + t cos²t – sint cos²t ) dt = 2 a³ (t²/2 + cost – 2t sint – 2cost + sin²t + t²/4 + t/4( sin2t ) +1/8 (cos2t) + 1/3 (cos³t)) = 2 a³(2² + 1 – 2 + ² + 1/8 +1/3 – 1 + 2 - 1/3 – 1/8) = 6³ a³.