
Учебное пособие по Н.Г
.pdf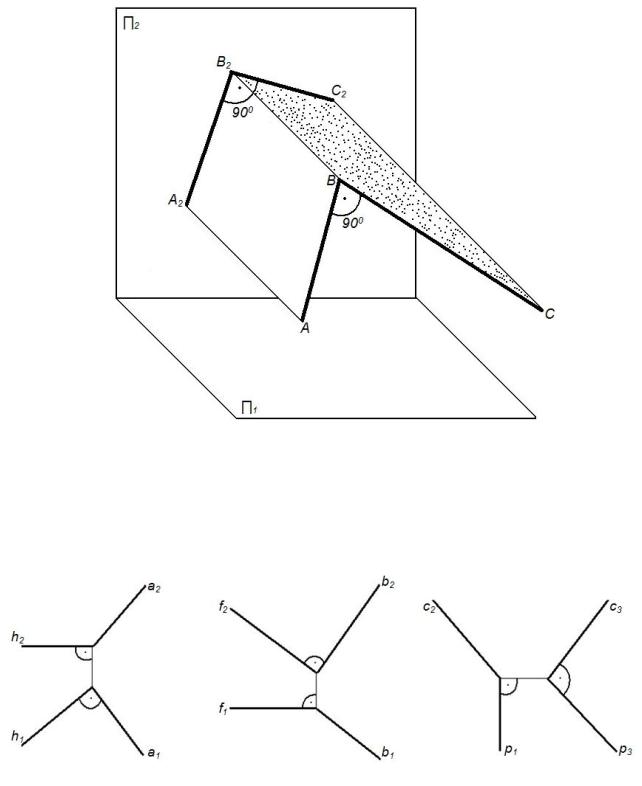
Рисунок 13 – Проецирование прямого угла
а) б) в)
Рисунок 14 – Комплексный чертеж взаимно перпендикулярных прямых
21
5 Плоскость
Проекцией любой плоскости является геометрическое место проекций всех ее точек. Если рассматривать плоскость, расположенную не перпендикулярно и не параллельно ни одной из плоскостей проекций, то ее проекции целиком заполнят собой поля плоскостей П1, П2, П3. Поэтому на комплексном чертеже задаются лишь некоторые геометрические элементы,
определяющее положение заданной плоскости в пространстве (таблица 1):.
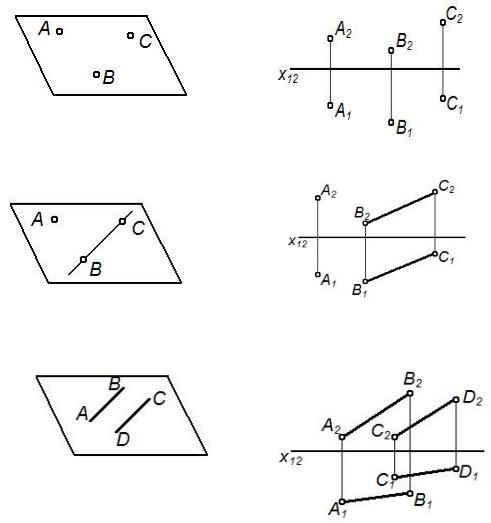
Таблица 1 – Способы задания плоскости
Задание |
Наглядное изображение |
Комплексный чертеж |
плоскости |
|
|
1 |
2 |
3 |
Тремя точками, |
|
|
не лежащими на |
|
|
одной прямой |
|
|
|
|
|
Прямой и |
|
|
точкой, не |
|
|
принадлежащей |
|
|
прямой |
|
|
|
|
|
Двумя |
|
|
параллельными |
|
|
прямыми |
|
|
|
|
|
22
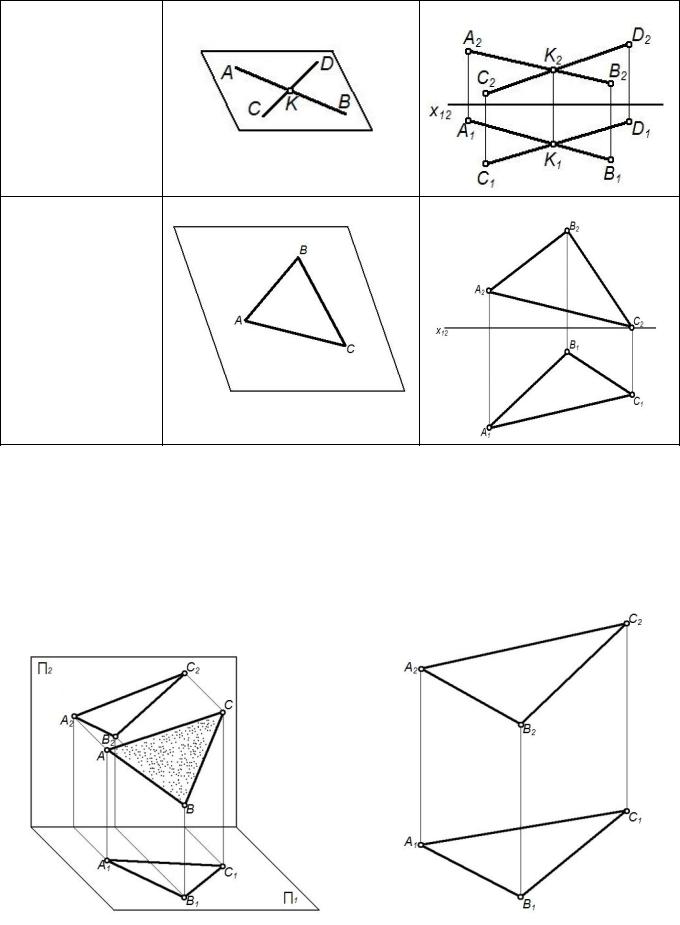
Двумя
пересекающимися
прямыми
Плоской фигурой
Возможны следующие положения плоскости относительно плоскостей проекции:
1) плоскость не перпендикулярна и не параллельна ни к одной плоскости проекций – общего положения (рисунок 15);
Рисунок 15 – Плоскость общего положения
23
2) плоскость перпендикулярна к какой-либо плоскости проекций -
проецирующая (рисунок 16);
Рисунок 16 – Проецирующая плоскость
3) плоскость параллельна какой-либо плоскости проекций (дважды проецирующая) – плоскость уровня (рисунок 17).
Рисунок 17 – Плоскость уровня
24
На комплексном чертеже рассматривается три проецирующих плоскости |
|||||||
и три плоскости уровня (таблица 2). |
|
|
|
|
|
||
Таблица 2 – Частные случаи расположения плоскостей |
|
|
|||||
|
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ |
|
|
||||
Горизонтально- |
Фронтально- |
|
|
Профильно- |
|
||
проецирующая |
проецирующая |
|
|
проецирующая плоскость |
|||
плоскость |
плоскость |
|
|
|
|
|
|
|
|
|
С2 |
|
В2 |
В3 |
|
В2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
А2 |
|
|
|
|
|
|
|
|
|
В2 |
|
|
А2 |
|
А3 |
|
С2 |
|
|
|
|
|
|
|
|
|
|
|
В1 |
С2 |
С3 |
|
|
|
|
|
|
|
|
|
А2 |
|
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
А1 |
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
|
|
В1 |
С1 |
|
С1 |
|
|
С1 |
|
|
|
|
|
|
|
||
|
А1 |
|
|
|
|
|
|
|
ПЛОСКОСТИ УРОВНЯ |
|
|
|
|||
Горизонтальная |
Фронтальная плоскость |
|
Профильная плоскость |
||||
плоскость уровня |
уровня |
|
|
|
уровня |
|
|
|
|
|
|
|
|
В3 |
|
А2 |
С2 |
В2 |
|
|
В2 |
|
С3 |
В2 |
|
|
|
|
|||
|
|
|
|
|
С2 |
|
|
|
|
|
С2 |
|
|
|
|
В |
А2 |
|
|
|
А2 |
|
|
|
|
|
|
|
А3 |
|
|
|
С1 |
|
|
|
А1 |
|
|
|
|
|
|
|
В1 |
|
|
А1 |
А1 |
В1 |
С1 |
|
|
|
|
|
|
|
|
|
С1 |
|
|
Горизонтально проецирующая плоскость - |
П1. Горизонтальная проекция |
||||||
такой плоскости |
вырождается в |
прямую линию |
(главная проекция). |
Это |
|||
|
|
25 |
|
|
|
|
|

главный признак горизонтально проецирующей плоскости на комплексном чертеже. Главная проекция плоскости обладает собирательными свойствами,
т.е. проекции всех точек принадлежащих горизонтально проецирующей
плоскости на П1 совпадают с главной проекцией этой плоскости.
Фронтально проецирующая плоскость - П2. Фронтальная проекция такой плоскости вырождается в прямую линию (главная прямая). Это признак фронтально проецирующей на комплексном чертеже. Главная проекция
(проекция на П2) обладает собирательным свойством, т.е. проекции всех точек,
принадлежащих фронтально проецирующей плоскости на П2 совпадают с главной проекцией этой плоскости.
Профильно проецирующая плоскость - П3. Профильная проекция такой плоскости вырождается в прямую линию (главная проекция). Это признак профильно проецирующей плоскости на комплексном чертеже. Главная проекция обладает собирательным свойством.
Горизонтальная плоскость уровня параллельна П1, одновременно такая плоскость является профильно и фронтально проецирующей.
Фронтальная плоскость уровня параллельна П2, одновременно горизонтально и профильно проецирующая плоскость.
Профильная плоскость уровня параллельна П3, одновременно горизонтально и фронтально проецирующая плоскость.
5.1Точка и линия в плоскости
Кчислу основных задач, решаемых на плоскости, относят:
-проведение любой прямой в плоскости;
-построение в плоскости некоторой точки;
-построение недостающей проекции точки;
-проверка принадлежности точки и плоскости.
Решение этих задач основывается на известных положениях геометрии:
26
- прямая принадлежит плоскости, если она проходит через две точки,
принадлежащих плоскости, или через точку в плоскости параллельно прямой,
лежащей в этой плоскости; - точка принадлежит плоскости, если через нее можно провести прямую,
принадлежащую плоскости.
Рассмотрим примеры:
а) Проведение любой прямой в плоскости
Рисунок 18 – Произвольная прямая в плоскости
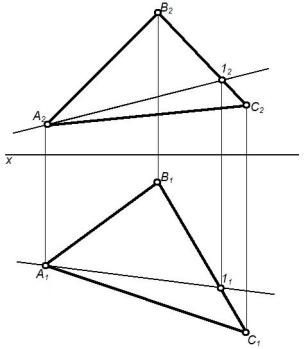
В плоскости АВС (рисунок 18) произвольно провести прямую через точку
А. Она будет пересекать сторону ВС в точке 1. А111 – горизонтальная проекция прямой, фронтальную проекцию А212 достроить на основании принадлежности прямой и точки.
В плоскости АВС (рисунок 19) через точку В провести прямую параллельную стороне АС. Проекции прямой В212 и В111 параллельны стороне
А2С2, А1С1.
27
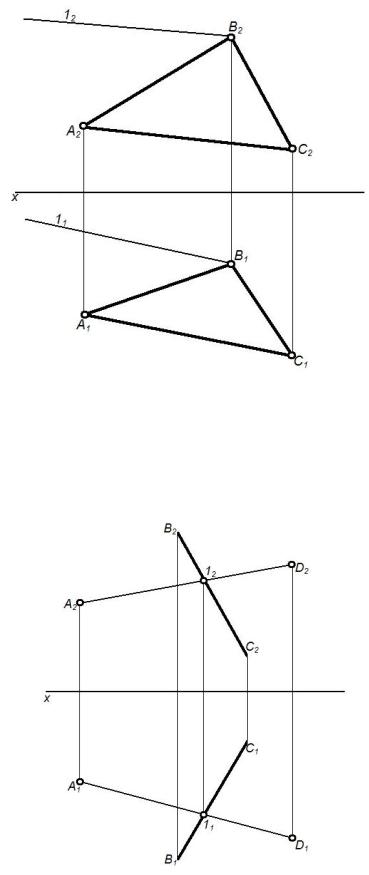
Рисунок 19 – Параллельная прямая в плоскости
б) построение в плоскости некоторой точки
Рисунок 20 – Точка в плоскости
28
Построение точки в заданной плоскости сводится к двум операциям:
-построению в плоскости вспомогательной прямой;
-построению точки на этой прямой.
В плоскости, заданной прямой ВС (В1С1; В2С2) и точкой А (А1; А2)
(рисунок 20), проводим вспомогательную прямую АD (A1D1; A2D2)
пересекающую прямую ВС (В1С1; В2С2) в точке 1 (11; 12). Полученные точки 1 и D принадлежат плоскости.
в) построение недостающей проекции точки
Рисунок 21 – Построение недостающей проекции точки
Плоскость задана проекциями треугольника АВС (А1В1С1, А2В2С2)
(рисунок 21). Принадлежащая этой плоскости точка D задана проекцией D2.
Следует достроить горизонтальную проекцию точки D (D1), для этого проводят вспомогательную прямую В2D2, проходящую через точку 12 принадлежащую
А2В2С2. Затем на плоскости П1 достраивают её горизонтальную проекцию 11 и
соединяют ее с точкой В1. На прямой В111 отмечают D1.
г) проверка принадлежности точки плоскости.
29

Для проверки в плоскости используют вспомогательную прямую,
принадлежащую плоскости.
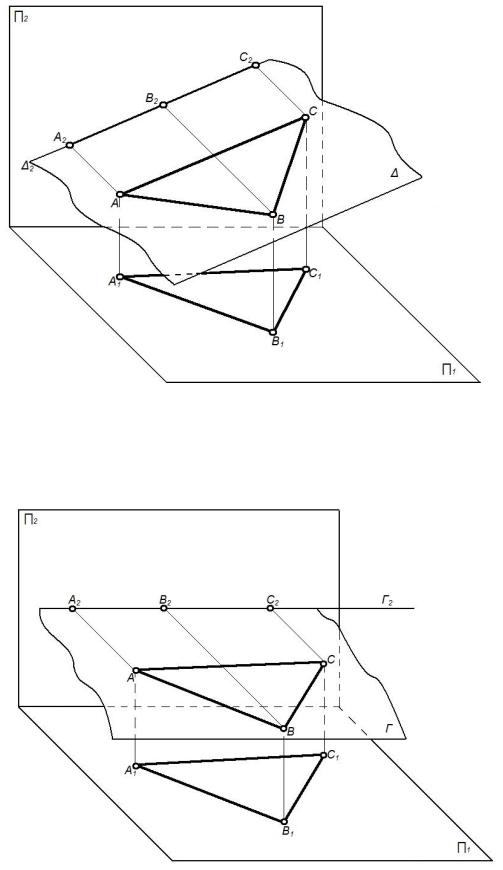
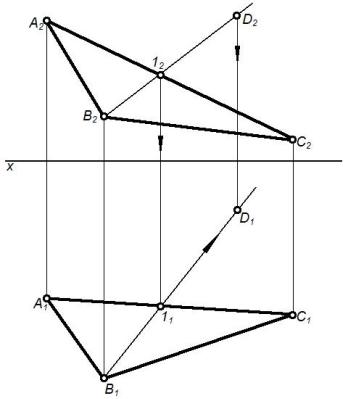
На рисунке 22 плоскость задана параллельными прямыми АВ (А1В1; А2В2)и
СD (С1D1; С2D2), и задана точка Е (Е2, Е1). Проводим через Е2 прямую 1222.
Убеждаемся, что горизонтальная проекция Е(Е1) не принадлежит 1121.
Следовательно, точка Е не принадлежит плоскости.
Рисунок 22 – Принадлежность точки плоскости
5.2Особые прямые на плоскости
Кпрямым, занимающим особое положение на плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций.
На рисунке 23 в плоскости треугольника АВС проведены горизонталь h
(h2, h1), фронталь f (f1, f2) и профильная прямая ВD (B1D1, B2D2).
30
