Раздел 1. Графическое оформление чертежей

Тема 1.3 Некоторые геометрические построения

Тема 1.4 Сопряжение линий

Тема 1.5 Построение уклона и конусности

Краткие теоретические сведения: геометрические построения широко применяется при решениях различных задач графическим способом с использованием чертежных инструментов. Точность чертежа зависит от правильности и аккуратности выполнения геометрических построений, таких как проведение параллельных и перпендикулярных линий, деление отрезка на равные части, построение и деление углов, деление окружностей на равные части, сопряжение. В очертаниях технических форм имеют место плавные переходы от одной линии к другой. Эти плавные переходы называются сопряжениями. Из всего многообразия сопряжений различных линий можно выделить следующие основные виды сопряжений: сопряжение прямой линии с дугой окружности, сопряжение двух различно расположенных прямых линий при помощи дуги окружности, сопряжение дуг двух окружностей при помощи прямых линий и сопряжение дуг двух окружностей при помощи третьей (рисунок 5). Дуги окружностей, при помощи которых выполняется сопряжение, называются дугами сопряжения. Для построения дуги сопряжения необходимо на чертеже выявить центр ее, радиус этой дуги и точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии. Задаваясь одним из этих параметров, остальные можно определить графически.

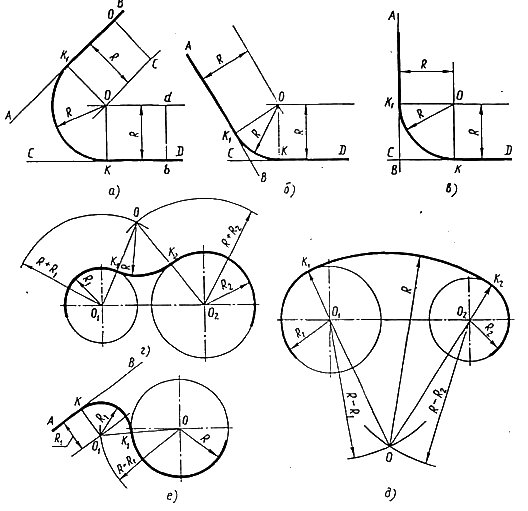
Рисунок 5 - а, б, в) сопряжение двух прямых линий, г) сопряжение дуг двух окружностей (внешнее), д) сопряжение дуг двух окружностей (внутреннее), е) сопряжение прямой линии с дугой окружности (внешнее).

Уклоном называют величину, характеризующую наклоном одной прямой линии к другой прямой. Уклон выражают дробью или в процентах. Уклоны применяются при вычерчивании деталей, например стальных балок и рельсов, изготовляемых на прокатных станах, и некоторых деталей, изготовленных литьем. Если уклон задается в процентах, например, 20, то линия уклона строится так же, как гипотенуза прямоугольного треугольника. Длину одного из катетов принимают равной 100, а другой-20. Очевидно, что уклон 20есть иначе уклон 1:5 (рисунок 6).

Рисунок 6 - построение уклона в частях и процентах.

Порядок выполнения:

1. На формате А3 построить рамку, тем самым, определить рабочее поле чертежа;

2. Вычертить основную надпись ГОСТ 2.104-95, форма 1;

3. Применив ГОСТ 2.303-68 выполнить чертеж проката по одному из вариантов (приложение В).

4. Проставить размеры, заполнить основную надпись.

5. Ответить на контрольные вопросы.

Исходные данные: Приложение В

Контрольные вопросы:

1. Что такое конусность, как её обозначают на чертеже?

2. Что такое уклон, как его обозначают на чертеже?

3. Что такое сопряжение?

4. Какие виды сопряжений вы знаете?

5. Какое сопряжение называется внешним, внутренним и смешанным?

6. Какими элементами определяется сопряжение?

Лист 4 «Сечение многогранника плоскостью»

Для выполнения задания необходимо изучить следующие разделы и темы дисциплины:

Раздел 2. Основы начертательной геометрии

Тема 2.1 Общие сведения о видах проецирования

Тема 2.2 Проецирование отрезка прямой линии

Тема 2.3 Проецирование плоских фигур

Тема 2.4 Способы преобразования проекций

Тема 2.5 Аксонометрические проекции

Тема 2.6 Проекции геометрических тел

Тема 2.7 Сечение геометрических тел плоскостями и развертки их поверхностей

Краткие теоретические сведения:

Изображения предметов на чертежах в соответствии с правилами государственного стандарта выполняют по способу (методу) прямоугольного проецирования. Проецированием называют процесс построения проекции предмета. Следовательно, чтобы построить проекцию какой-либо фигуры на плоскости, необходимо через точки этой фигуры провести воображаемые проецирующие лучи до их пересечения с плоскостью. Проекции всех точек фигуры образуют проекцию заданной фигуры (рисунок 7).

Рисунок 7

Прямоугольное проецирование широко используется для построения изображений на чертежах. Наиболее удобной для фиксирования положения геометрической фигуры в пространстве и выявления ее формы по ортогональным (прямоугольным) проекциям является, декартова система координат, состоящих из трех взаимно перпендикулярных плоскостей проекций. Для удобства проецирования в качестве трех плоскостей проекций выбирают три взаимно перпендикулярные плоскости. Одну из них принято располагать горизонтально - ее называют горизонтальной плоскостью проекций (H), другую - вертикально, параллельно плоскости чертежа, ее называют фронтальной плоскостью проекций (V) и третью, перпендикулярно двум имеющимся - ее называют профильной плоскостью проекций (W). Эти плоскости проекций пересекаются по линиям, называемыми осями проекций: x, y, z (рисунок 8).

Рисунок 8

Многие окружающие нас предметы и имеют форму геометрических тел или их сочетаний. Форма деталей, встречающихся в технике, также представляет собой сочетание различных геометрических тел или их частей. Геометрические тела — это замкнутая часть пространства, ограниченная плоскими или кривыми поверхностями, все тела делятся на многогранники и тела вращения. Геометрические тела ограниченные со всех сторон плоскостями называются многогранниками.

Геометрические тела образованные за счет вращения какой либо линии (образующая, меридиан), вокруг неподвижной оси (ось вращения) называются телами вращения. Форма каждого геометрического тела и его изображений на чертеже имеет свои характерные признаки. Этим пользуются, чтобы облегчить чтение и выполнение чертежей (рисунок 9).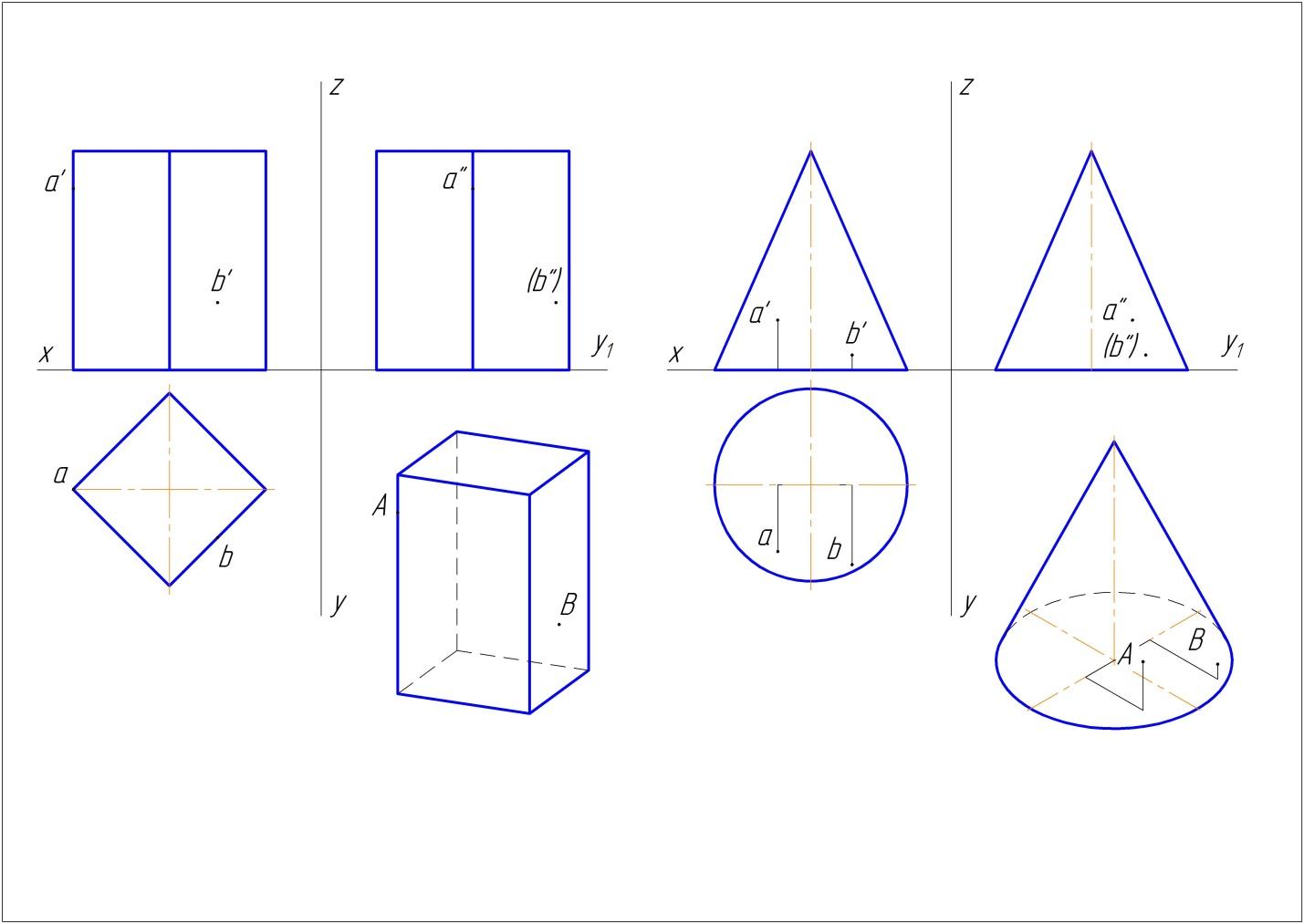

Рисунок 9 – проекции геометрических тел

Детали машин и приборов часто имеют формы, представляющие собой различные геометрические поверхности, рассечённые плоскостями. Сечение поверхности геометрических тел плоскостью называется плоская фигура, точки которой принадлежат и поверхности тела, и секущей плоскости. Кроме того, иногда необходимо выполнить развертки поверхности полых деталей, усеченных плоскостью.

Развертка – плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью. Построение прямоугольных и аксонометрических проекций усеченных тел, а также определение истинного вида сечений и разверток поверхностей геометрических тел часто используется на практике (рисунок 10).

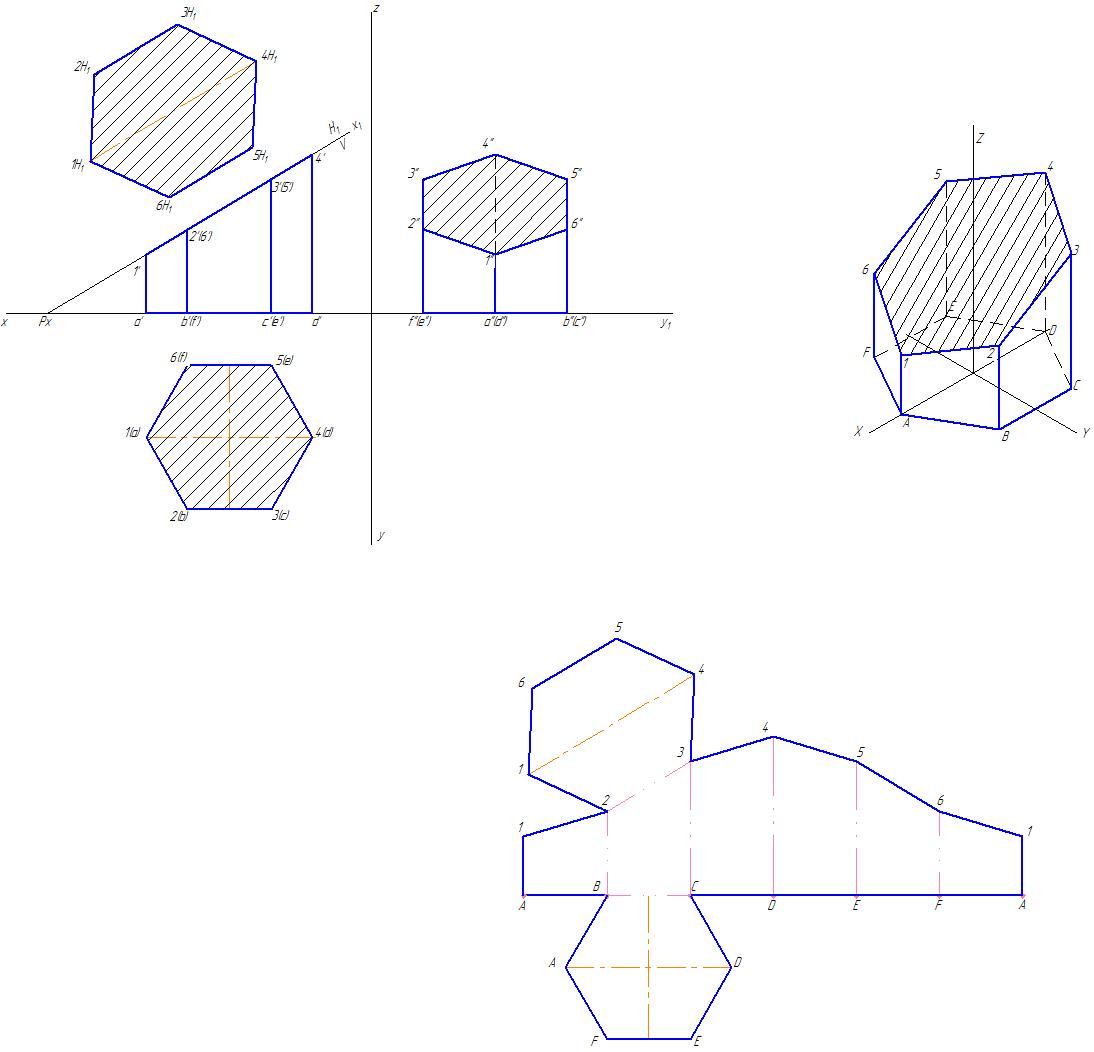
Рисунок 10 - прямоугольная проекция усечённой призмы и натуральная величина фигуры сечения, аксонометрическая проекция усеченной призмы, развертка усеченной призмы.

Порядок выполнения:

1. На формате А3 построить рамку, тем самым, определить рабочее поле чертежа;

2. Вычертить основную надпись ГОСТ 2.104-95, форма 1;

3. По заданным параметрам, построить прямоугольную проекцию усеченной призмы и найти натуральную величину фигуры сечения;

4. По комплексному чертежу построить аксонометрию усеченной модели;

5. Построить развертку усеченной призмы.

6. Ответить на контрольные вопросы.

Исходные данные: Приложение Г

Контрольные вопросы:

1. Какими приемами определяют недостающие проекции точек, лежащих на поверхности пирамиды и конуса?

2. Какие тела называются телами вращения?

3. Чем отличается пирамида от призмы?

4. Какие геометрические тела вам известны?

5. В чем отличие прямоугольной проекции предмета от аксонометрической?

6. Сечение призмы проецирующей плоскостью, как строится проекция сечения и как определяется натуральная величина фигуры сечения?

7. Прямоугольное проецирование, что это такое и где его используют?

8. Какие установлены виды аксонометрических проекций?

9. Что такое развертка?

10. Как вычерчиваются линии сгиба с учетом ГОСТ 2.303-68.

Лист 5 «Проекции геометрических тел»

Для выполнения задания изучается тот же раздел и те же темы, что и для выполнения четвертого задания.

Порядок выполнения:

1. На формате А3 построить рамку, тем самым, определить рабочее поле чертежа;

2. Вычертить основную надпись ГОСТ 2.104-95, форма 1;

3. По заданным параметрам, построить прямоугольную проекцию геометрического тела;

4. По комплексному чертежу построить аксонометрию модели.

Исходные данные: Приложение Д

Лист 6 «Виды и разрезы»

Для выполнения задания необходимо изучить следующие разделы и темы дисциплины: