
КЛА ЭКЗик / 5лек
.docxФазирование за счет ожидания на старте.
Подобный маневр производится и в том случае, когда при фазировании по схеме космос-космос хотят избежать объемного маневра. Разница только в том, что ТК выводится не в точку встречи, а в плоскость ОС.
Время полета ТК с момента старта до момента встречи
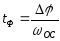 ,
,
за это время долготное расстояние между долготой стартовой позицией и долготой следа траектории ОС будет равно
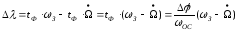
Из
треугольника
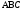 по теореме синусов запишем
по теореме синусов запишем
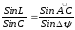
откуда
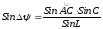
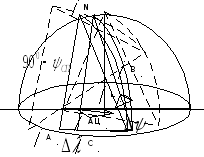
Рис. 3 Схема маневра посхеме Земля – космос.
где А- точка стояния стартовой позиции,
В – точка встречи ТК и ОС,
С – точка пересечения следа траектории ОС и широты стартовой
позиции,
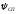 -
географическая широта стартовой позиции,
-
географическая широта стартовой позиции,
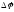 -
фазовое рассогласование между положением
ОС и точкой
-
фазовое рассогласование между положением
ОС и точкой
встречи,
Найдем
экстремальные значения угла
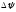 ,
для чего продифференцируем полученное
выражение по L, получим
,
для чего продифференцируем полученное
выражение по L, получим
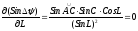
что справедливо в случае
-
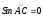 след
траектории проходит через точку стояния
стартовой позиции.
след
траектории проходит через точку стояния
стартовой позиции.
-
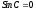 угол
С равен сумме угла азимута, отсчитываемого
от меридиана, и прямого угла, равенство
этой суммы нулю возможно только в
случае, если орбита ОС совпадает с
плоскостью экватора.
угол
С равен сумме угла азимута, отсчитываемого
от меридиана, и прямого угла, равенство
этой суммы нулю возможно только в
случае, если орбита ОС совпадает с
плоскостью экватора.
-
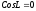 ,
что возможно при
,
что возможно при
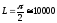 км.
км.
Из
треугольника
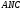 по теореме косинусов получим
по теореме косинусов получим
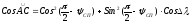
тогда
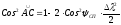
преобразуя,
получим
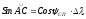
Поскольку
значения
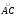 и
и
 малы, то выражение можно представить
в виде
малы, то выражение можно представить
в виде
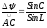
или
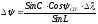
подставляя,
значение
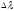 получим, с учетом
получим, с учетом
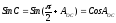 ,
,
где
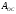 азимут ОС, тогда окончательно получим
азимут ОС, тогда окончательно получим
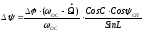
где
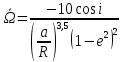
Полученное выражение позволяет определить соотношения между параметрами ТК и ОС, позволяющие осуществить фазирование за счет ожидания на старте.


