21. Какие применяют методы нормировки по частоте. Их суть.

Чтобы упростить сопоставление частотных характеристик ЦФ с различными 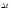_{(шаг дискретизации)}, применяют нормировку частоты. Существует два способа нормировки. При первом способе полагают нормированной частоту ₍частоты ₎, тогда период частотных характеристик равен и требования к ним задаются на интервале . При втором способе используют нормированную частоту . В этом случае период частотных характеристик равен единице и требования к ним задаются на интервале . При этом изменяются аргументы в обозначении частотных характеристик: амплитудно-частотной характеристики, фазочастотной характеристикой, передаточные функции. (₎. Изменяются и сами формулы частотных характеристик.

_{Выражения для АЧХ и ФЧХ НЦФ при нормированной частоте :}

22. С какой целью применяют преобразование схем цф

Существует весьма большое число различных форм реализации РЦФ и НЦФ. Рассмотрим наиболее распространенные из них. При построении структурных схем, соответствующих этим формам реализации, будем использовать обозначения операций, широко используемых в теории управления. Операцию задержки (запоминания) отсчетов сигнала на шагов дискретизации обозначим квадратиком с записью в нем величины , операцию сложения нескольких слагаемых ‒ прямоугольником со знаком 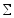, а операцию умножения на константу ‒ квадратиком с крестиком внутри. Передачу данных будем отображать на схемах сплошными линиями со стрелками.

Для сравнительного анализа сложности реализации различных форм передаточных функций обычно используют следующие реализационные характеристики:

‒ число ячеек (регистров) оперативной памяти, необходимой для хранения отсчетов входного сигнала и промежуточных результатов;

‒ число ячеек постоянной памяти, необходимой для хранения коэффициентов фильтра;

‒ число умножений, выполняемых при вычислении одного отсчета выходного сигнала;

‒ число алгебраических сложений двух слагаемых, которые должны быть выполнены в фильтре для получения одного отсчета выходного сигнала.

Для рекурсивных фильтров можно выделить четыре основные формы реализации: прямую, каноническую, каскадную (последовательную) и параллельную.

Прямая форма (рис. 8.1) соответствует непосредственной реализации

передаточной функции:

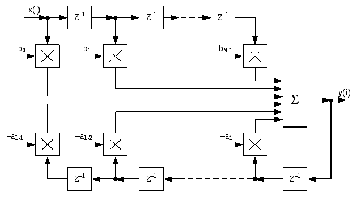
Каноническая форма

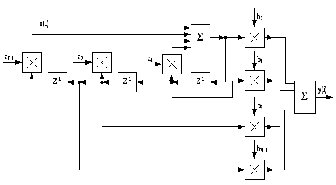
Введение вспомогательной последовательности позволяет объединить часть элементов задержки и уменьшить их число по сравнению с прямой формой реализации. Остальные реализационные характеристики при этом остаются без изменения.

При последовательной форме используется способ представления в виде произведения типовых звеньев не выше второго порядка (биквадратных звеньев)

Реализационные характеристики этой формы во многом зависят от числа используемых биквадратных звеньев.

Параллельная форма основана на эквивалентном представлении суммой типовых звеньев, которые могут быть реализованы в виде биквадратного блока при . Реализационные характеристики здесь также сильно зависят от числа типовых блоков.

Все рассмотренные формы реализации РЦФ при одних и тех же входных данных и бесконечной разрядности представления чисел в ЦФ дают абсолютно одинаковые результаты, так как получены путем эквивалентных математических преобразований одного и того же исходного уравнения. Однако при ограниченной разрядной сетке представления чисел, что всегда имеет место в реальных ЦФ, эти формы приведут к различному результату, так как отличаются механизмом преобразования погрешностей округления. Каскадная форма, как правило, обеспечивает наименьший уровень собственных шумов фильтра.

Для нерекурсивных ЦФ возможны прямая и каскадная формы реализации. Каскадную форму легко получить из каскадной формы РЦФ, если в биквадратных звеньях положить все коэффициенты равными нулю. Для весьма важного типа нерекурсивных фильтров с линейной фазочастотной характеристикой возможны специальные формы реализации, учитывающие свойства симметрии или антисимметрии коэффициентов фильтра . В таких формах реализации число умножений уменьшается практически вдвое. В два раза сокращается и число хранимых в памяти фильтра констант.