2. Расчетная часть

2.1. Построение математической модели

Задача № 10

Аэрофлот имеет пять типов самолетов и обслуживает пять маршрутов. Известны затраты на эксплуатацию каждого вида самолета на каждом маршруте и прибыль, получаемая при выполнении данного маршрута.

Распределить самолеты по маршрутам так, чтобы суммарная чистая прибыль была максимальна.

Составим математическую модель.

1. Введем переменные данной задачи:

• aij – затраты на j самолет по i маршруту;

• j – самолет;

• i – маршрут;

• mi - прибыль от одного маршрута;

• xij – полетит ли j самолет по i маршруту

2. Составим матрицу затрат на эксплуатацию

   i/j	j1	j2	j3	j4	j5
   i1	200	300	300	350	200
   i2	400	350	200	250	350
   i3	350	400	500	450	500
   i4	200	300	400	450	250
   i5	300	200	450	350	400

3. Чистая прибыль = прибыль – затраты

4. Ограничение:

b_j – max затраты на каждый j самолет

записываем общий вид уравнений ограничения:

a₁₁*x₁₁+…+a_ji+x_ji≤

…

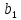
a_ji*x_ji+…+ a_ji+x_ji≤ b_j

5. Сумма уравнений:

L(x) = (1000-200) x₁₁ + (1200-400)*x₁₂ +(900-350)*x₁₃ +(1500-200)*x₁₄ +(1600-300)*x₁₅ +(1000-300)*x₂₁+(1200-350)*x₂₂+(900-400)*x₂₃+(1500-300)*x₂₄+(1600-200)*x₂₅+(1000-300)*x₃₁ +(1200-200)*x₃₂ +(900-500)*x₃₃ +(1500-400)*x₃₄ +(1600-450)*x₃₅ +(1000-350)*x₄₁ +(1200-250)*x₄₂ +(900-450)*x₄+(1500-450)*x₄₄+(1600-350)*x₄₅ +(1000-200)*x₅₁ +(1200-350)*x₅₂ +(900-500)*x₅₃ +(1500-250)*x₅₄+(1600-400)*x₅₅

Целевая функция - L(x) =

2.2. Решение задачи

Первый вариант решения задачи №10. Венгерский метод.

Исходная матрица имеет вид:

200	300	300	350	200
400	350	200	250	350
350	400	500	450	500
200	300	400	450	250
300	200	450	350	400

Модифицируем матрицу умножением всех элементов на (-1) и затем сложением их с максимальным элементом матрицы (500) так, чтобы матрица не содержала бы отрицательных элементов:

300	200	200	150	300
100	150	300	250	150
150	100	0	50	0
300	200	100	50	250
200	300	50	150	100

1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

150	50	50	0	150	150
0	50	200	150	50	100
150	100	0	50	0	0
250	150	50	0	200	50
150	250	0	100	50	50

Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:

150	0	50	0	150
0	0	200	150	50
150	50	0	50	0
250	100	50	0	200
150	200	0	100	50
0	50	0	0	0

После вычитания минимальных элементов получаем полностью редуцированную матрицу.

2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.

Фиксируем нулевое значение в клетке (1, 2). Другие нули в строке 1 и столбце 2 вычеркиваем.

Фиксируем нулевое значение в клетке (2, 1). Другие нули в строке 2 и столбце 1 вычеркиваем.

Фиксируем нулевое значение в клетке (3, 5). Другие нули в строке 3 и столбце 5 вычеркиваем.

Фиксируем нулевое значение в клетке (4, 4). Другие нули в строке 4 и столбце 4 вычеркиваем.

Фиксируем нулевое значение в клетке (5, 3). Другие нули в строке 5 и столбце 3 вычеркиваем.

В итоге получаем следующую матрицу:

150	[0]	50	[-0-]	150
[0]	[-0-]	200	150	50
150	50	[-0-]	50	[0]
250	100	50	[0]	200
150	200	[0]	100	50

Количество найденных нулей равно k = 5. В результате получаем эквивалентную матрицу Сэ:

150	0	50	0	150
0	0	200	150	50
150	50	0	50	0
250	100	50	0	200
150	200	0	100	50

4. Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить максимальное значение прибыли.

150	[0]	50	[-0-]	150
[0]	[-0-]	200	150	50
150	50	[-0-]	50	[0]
250	100	50	[0]	200
150	200	[0]	100	50

Cmax = 500 + 300 + 400 + 450 + 450 = 2100

Второй вариант решения задачи № 10.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов. Для решения задачи методом потенциалов нужно ввести дополнительные данные в матрицу тарифов.

	1	2	3	4	5	Запасы
1	200	300	300	350	200	1
2	400	350	200	250	350	1
3	350	400	500	450	500	1
4	200	300	400	450	250	1
5	300	200	450	350	400	1
Потребности	1	1	1	1	1

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 1 + 1 + 1 + 1 + 1 = 5

∑b = 1 + 1 + 1 + 1 + 1 = 5

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Занесем исходные данные в распределительную таблицу.

	1	2	3	4	5	Запасы
1	200	300	300	350	200	1
2	400	350	200	250	350	1
3	350	400	500	450	500	1
4	200	300	400	450	250	1
5	300	200	450	350	400	1
Потребности	1	1	1	1	1

Этап I. Поиск первого опорного плана.

1. Используя метод наибольшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наибольшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.

Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наибольшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

	1	2	3	4	5	Запасы
1	200	300[1]	300	350	200	1
2	400[1]	350	200	250	350	1
3	350	400	500	450	500[1]	1
4	200	300	400	450[1]	250	1
5	300	200	450[1]	350	400	1
Потребности	1	1	1	1	1

2. Подсчитаем число занятых клеток таблицы, их 5, а должно быть m + n - 1 = 9. Следовательно, опорный план является вырожденным.

Строим новый план.

Значение целевой функции для этого опорного плана равно:

L(x) = 300*1 + 400*1 + 500*1 + 450*1 + 450*1 = 2100

	1	2	3	4	5	Запасы
1	200	300[1]	300	350	200	1
2	400[1]	350	200	250	350	1
3	350	400	500	450	500[1]	1
4	200	300	400	450[1]	250	1
5	300	200	450[1]	350	400	1
Потребности	1	1	1	1	1

Подсчитаем число занятых клеток таблицы, их 5, а должно быть m + n - 1 = 9. Следовательно, опорный план является вырожденным.

Значение целевой функции для этого опорного плана равно:

L(x) = 300*1 + 400*1 + 500*1 + 450*1 + 450*1 = 2100

Для получения невырожденного плана принудительно добавляем нуль [0] в клетку (1;1); (1;3); (1;4); (1;5);

Возвращаемся к плану №0

	1	2	3	4	5
1	200[0]	300[1]	300[0]	350[0]	200[0]
2	400[1]	350	200	250	350
3	350	400	500	450	500[1]
4	200	300	400	450[1]	250
5	300	200	450[1]	350	400

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 200; 0 + v₁ = 200; v₁ = 200

u₂ + v₁ = 400; 200 + u₂ = 400; u₂ = 200

u₁ + v₂ = 300; 0 + v₂ = 300; v₂ = 300

u₁ + v₃ = 300; 0 + v₃ = 300; v₃ = 300

u₅ + v₃ = 450; 300 + u₅ = 450; u₅ = 150

u₁ + v₄ = 350; 0 + v₄ = 350; v₄ = 350

u₄ + v₄ = 450; 350 + u₄ = 450; u₄ = 100

u₁ + v₅ = 200; 0 + v₅ = 200; v₅ = 200

u₃ + v₅ = 500; 200 + u₃ = 500; u₃ = 300

	v1=200	v2=300	v3=300	v4=350	v5=200
u1=0	200[0]	300[1]	300[0]	350[0]	200[0]
u2=200	400[1]	350	200	250	350
u3=300	350	400	500	450	500[1]
u4=100	200	300	400	450[1]	250
u5=150	300	200	450[1]	350	400

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(5;5): 150 + 200 < 400; ∆₅₅ = 150 + 200 - 400 = -50

Выбираем максимальную оценку свободной клетки (5;5): 400

Для этого в перспективную клетку (5;5) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

	1	2	3	4	5	Запасы
1	200[0]	300[1]	300[0][+]	350[0]	200[0][-]	1
2	400[1]	350	200	250	350	1
3	350	400	500	450	500[1]	1
4	200	300	400	450[1]	250	1
5	300	200	450[1][-]	350	400[+]	1
Потребности	1	1	1	1	1

Цикл приведен в таблице (5,5 → 5,3 → 1,3 → 1,5).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 5) = 0. Прибавляем 0 к объемам грузов, стоящих в плюсовых клетках и вычитаем 0 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

	1	2	3	4	5	Запасы
1	200[0]	300[1]	300[0]	350[0]	200	1
2	400[1]	350	200	250	350	1
3	350	400	500	450	500[1]	1
4	200	300	400	450[1]	250	1
5	300	200	450[1]	350	400[0]	1
Потребности	1	1	1	1	1

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 200; 0 + v₁ = 200; v₁ = 200

u₂ + v₁ = 400; 200 + u₂ = 400; u₂ = 200

u₁ + v₂ = 300; 0 + v₂ = 300; v₂ = 300

u₁ + v₃ = 300; 0 + v₃ = 300; v₃ = 300

u₅ + v₃ = 450; 300 + u₅ = 450; u₅ = 150

u₅ + v₅ = 400; 150 + v₅ = 400; v₅ = 250

u₃ + v₅ = 500; 250 + u₃ = 500; u₃ = 250

u₁ + v₄ = 350; 0 + v₄ = 350; v₄ = 350

u₄ + v₄ = 450; 350 + u₄ = 450; u₄ = 100

	v1=200	v2=300	v3=300	v4=350	v5=250
u1=0	200[0]	300[1]	300[0]	350[0]	200
u2=200	400[1]	350	200	250	350
u3=250	350	400	500	450	500[1]
u4=100	200	300	400	450[1]	250
u5=150	300	200	450[1]	350	400[0]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.

Максимальная прибыль составит:

L(x) = 300*1 + 400*1 + 500*1 + 450*1 + 450*1= 2100

Анализ

Венгерский метод является одним из интереснейших и наиболее распространенных методов решения транспортных задач. Венгерский алгоритм — алгоритм оптимизации, решающий задачу о назначениях за полиномиальное время. Он был разработан и опубликован Харолдом Куном в 1955 году. Автор дал ему имя «венгерский метод» в связи с тем, что алгоритм в значительной степени основан на более ранних работах двух венгерских математиков.

Метод потенциалов предназначен для решения транспортной задачи в матричной постановке. Потенциалы — это двойственные переменные. Сам метод — прямой, на каждом шаге выбирается одно из двойственных ограничений, которое не выполняется и исправляется таким образом, чтобы не нарушить ограничения прямой задачи. Постепенно в двойственной задаче ограничения будут выполнены, что будет означать оптимальность в прямой задаче.

Исходя из условия задачи №10 можно сказать что это задача о назначениях в большей степени, чем стандартная транспортная задача. В наиболее общей форме задача формулируется следующим образом: имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой (но только одной) работы, но с неодинаковыми затратами. Нужно распределить работы так, чтобы выполнить работы с минимальными затратами.

Если число работ и исполнителей совпадает, то задача называется линейной задачей о назначениях. Обычно, если говорят о задаче о назначениях без дополнительных условий, имеют ввиду линейную задачу о назначениях. Данная задача без дополнительных условии поэтому венгерский метод более подходящий для решения такого вида задач. Он менее громоздкий и не требует добавления условий. Метод потенциалов же подразумевает введение в условие линейной задачи о назначениях дополнительных условий, что делает решение более громоздким. Другие методы решения транспортных задач не подходят для решения задачи №10 так как требуют введения большого количества дополнительных условий и решение их очень громоздкое.