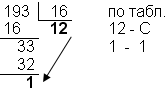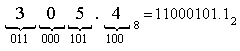Тема 1. Системы счисления
Таблица 1. Наиболее важные системы счисления.
|
Двоичная (Основание 2) |
Восьмеричная (Основание 8) |
Десятичная (Основание 10) |
Шестнадцатиричная (Основание 16) | ||
|
|
триады |
|
тетрады | ||
|
0 1 |
0 1 2 3 4 5 6 7 |
000 001 010 011 100 101 110 111 |
0 1 2 3 4 5 6 7 8 9 |
0 1 2 3 4 5 6 7 8 9 10-A 11-B 12-C 13-D 14-E 15-F |
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
При переводе чисел из одной системы счисления в другую следует придерживаться следующих правил:
Перевод чисел в десятичную системуосуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример. 7 6 5 4 3 2 1 0
1)
Перевести 10101101
"10"
с.с.
101011012=
1
27+
0
26+
1
25+
0
24+
1
23+
1
22+
0
21+
1
20=
= 1*128+0 + 32 + 0 + 8 + 4 + 0 + 1 = 17310
2)
Перевести 10102
"10"
с.с.
1010 (2)= 1*23+ 1*21= 8+2 =10(10) ;
3) Перевести 1011012 =
"10"
с.с.
1011012 = 1*25+0*24+1*23+1*22+0*21+1*20= 32+0+8+4+2+1=45(10)
в)
Перевести 703,048
"10"
с.с.
703,048= 7
82+
0
81+
3
80+
0
8-1+
4
8-2= 451,062510
=7*64 + 0 + 3 + 0 + 4*(1/64) =
448 0,0625
4)
Перевести С716
"10"
с.с.
С7(16)= 12*161+ 7*160= 192 + 7 =199(10) ;
12-C
5)
Перевести B2E,416
"10"
с.с.
B2E,416=
11
162+
2
161+
14
160+
4
16-1= 2862,2510
11-B 14-E по таблице
6)
Перевести 3018
"10"
с.с.
7)
Перевести С116
"10"
с.с.
12-C
8)
Перевести 110,0012
"10"
с.с.
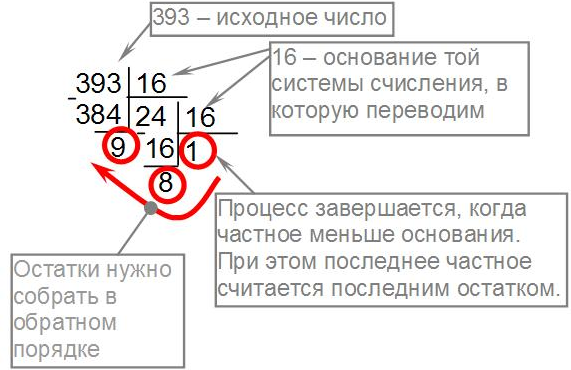
Перевод десятичных чисел в недесятичную системусчисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
|
Пример. 1) Перевести
18110 Результат: 18110= 2658
|
2) Перевести
62210 Результат: 62210= 26E16
|
3)
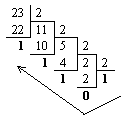
Перевести 2310
Результат: 2310= 101112
|
|
4) Перевести
2510
Результат: 110012 |
5)
Перевести 19310
Результат: 110000012
|
6)
Перевести 19310
Результат: 3018
|
|
7)
Перевести 19310
Результат: С116
|
|
9)
Перевести 7510
|
"8"
с.с.
"16"
с.с.
«2» с.с
«2» с.с
«2» с.с.
«8» с.с.
«16» с.с.
«2» с.с.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
|
Пример. 1) Перевести
305,48
|
2) Перевести
7B2,E16
|
"2"
с.с.
"2"
с.с.
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системепоступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример.
1)
Перевести 110000012
"8"
с.с.
=
3018
2)
Перевести 11001112
"8"
с.с.
11001112= 001 100 1112 = 1478.
3)
Перевести 1101111001,11012
"8"
с.с.
4)
Перевести 11111111011,1001112
"16"
с.с.
1 5 Е С
5)
Перевести 11001111010 1110(2)
"16"
с.с.
11001111010 1110(2)= 0110 0111 1010 1110(2)= 67AЕ(16).
6 7 А Е
6)
Перевести 11111111011,1001112
"16"
с.с.
Перевод из восьмеричной в шестнадцатеричную систему и обратноосуществляется через двоичную систему с помощью триад и тетрад.
Пример.
Перевести 175.248
"16"
с.с.
Результат: 175,248= 7D,516.