
АГ Векторная алгебра 2015-16 / Практическое занятие 3+СР(координаты вектора)
.docПрактическое занятие № 3
(Координаты вектора)
-
Найдите координаты точки M, делящей отрезок, ограниченный точками M1(2; 3) и M2(–5; 1), в отношении: 1)
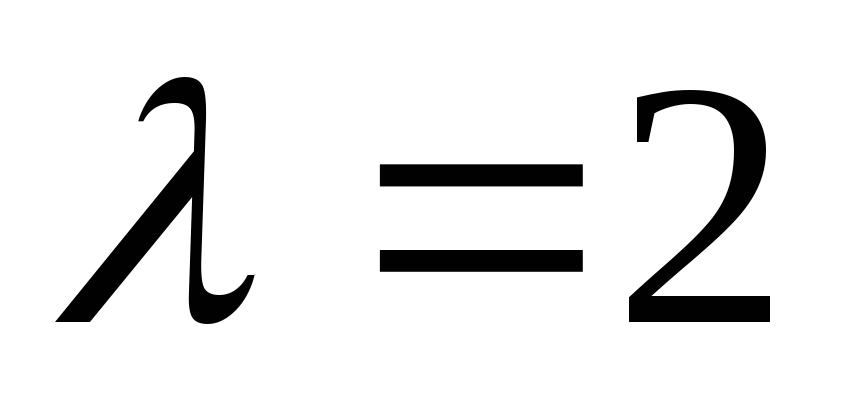 ,
2)
,
2)
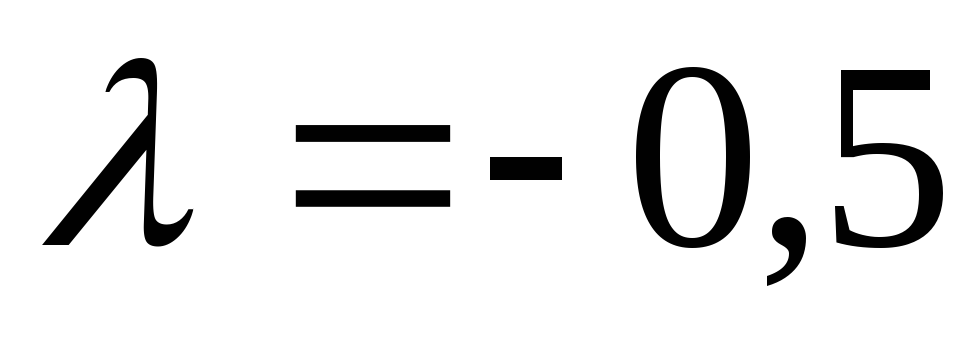 ,
3)
,
3)
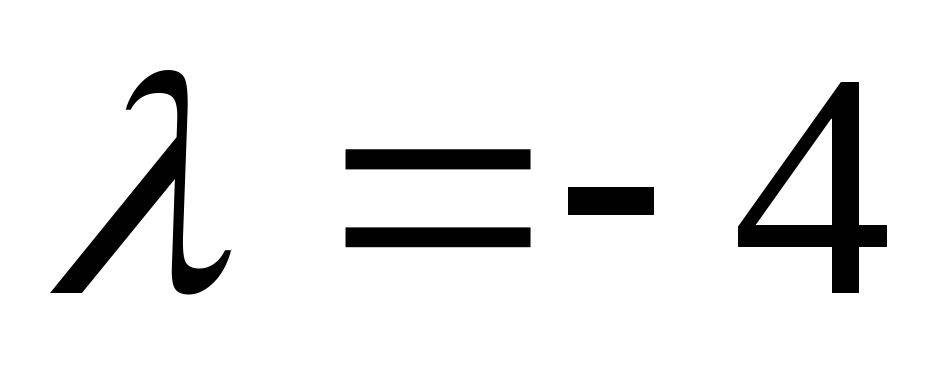 ,
4)
,
4)
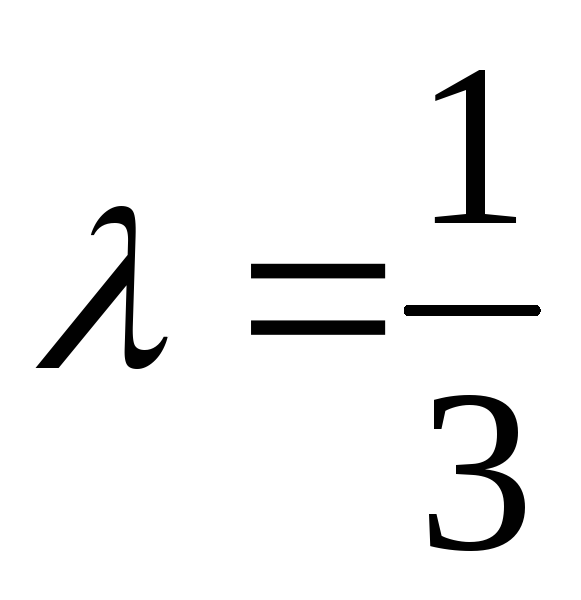 .
.
Ответ: 1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() .
.
-
Пусть в данной аффинной системе координат даны точки
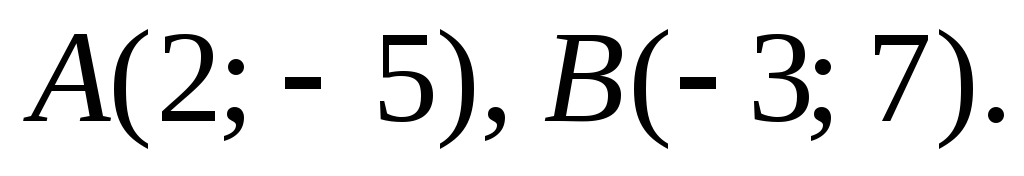 Точки C,
D,
E
делят отрезок AB
на четыре равные части. Найти координаты
этих точек.
Точки C,
D,
E
делят отрезок AB
на четыре равные части. Найти координаты
этих точек.
Ответ:
![]() ,
,
![]() ,
3)
,
3)
![]() .
.
-
Найти длины векторов, заданных своими координатами в ПДСК:
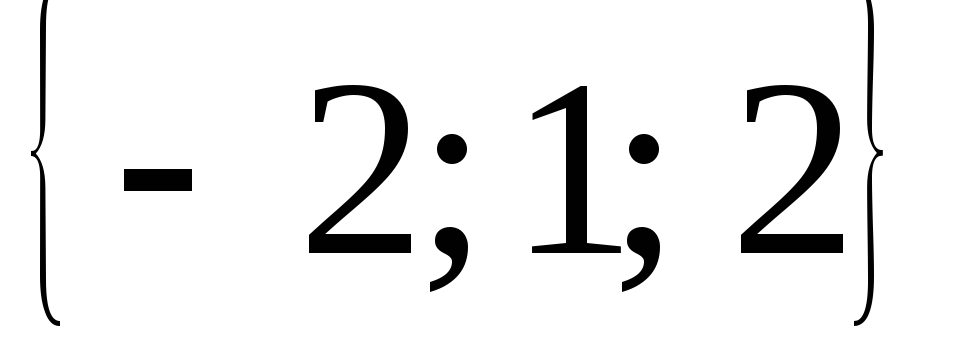 ,
,
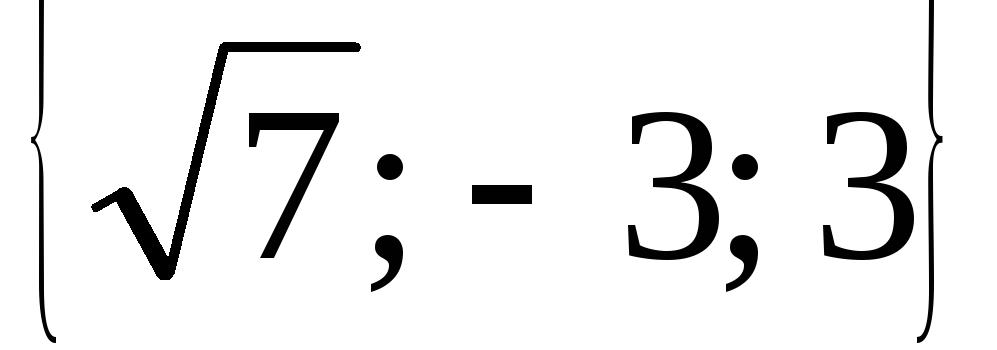 ,
,
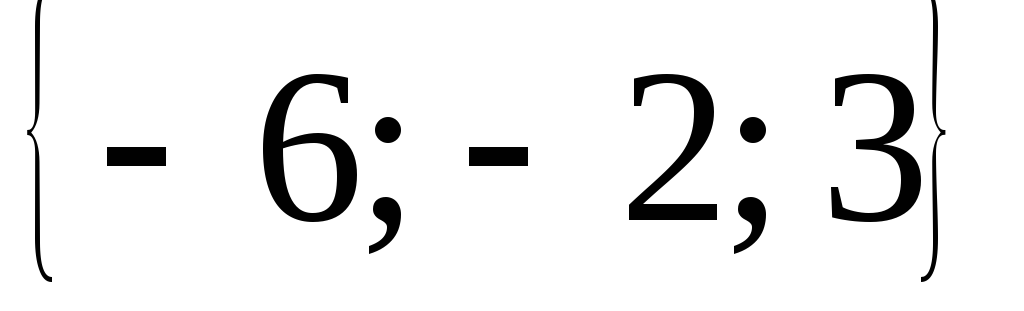 ,
,
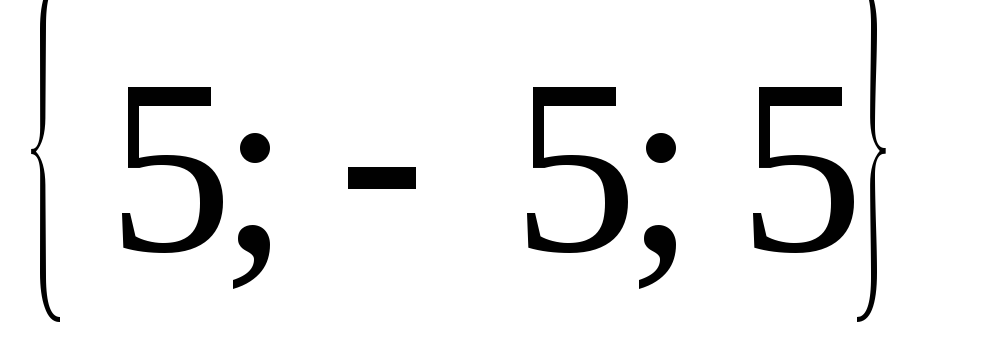 ,
,
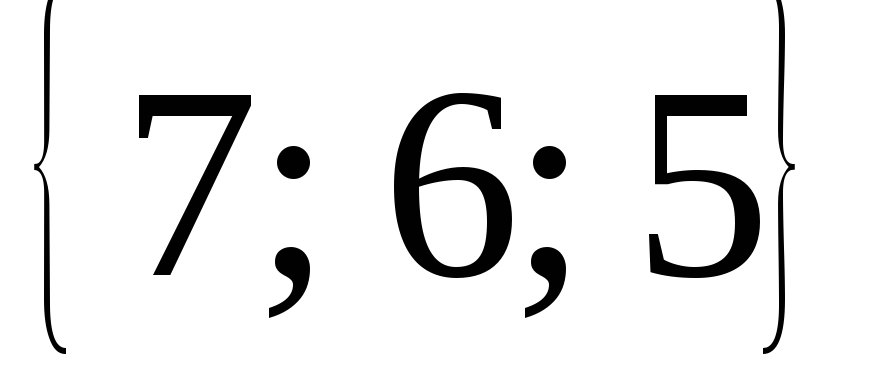 .
.
Ответ:
![]() .
.
-
Даны векторы
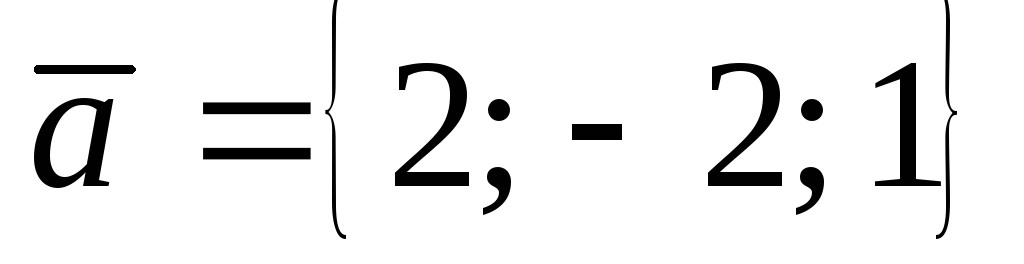 ,
,
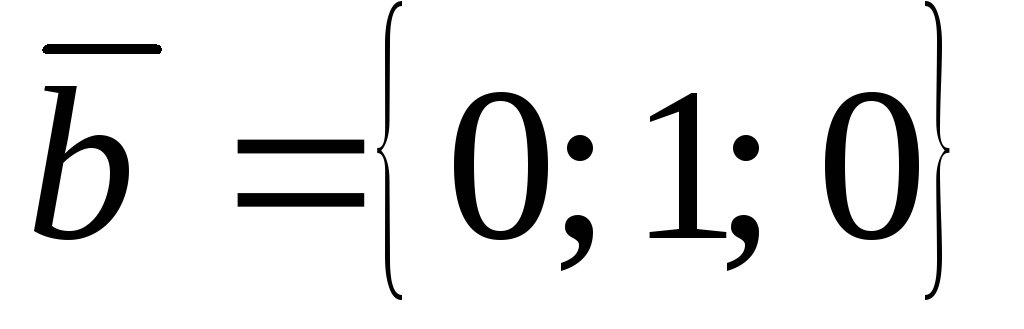 ,
,
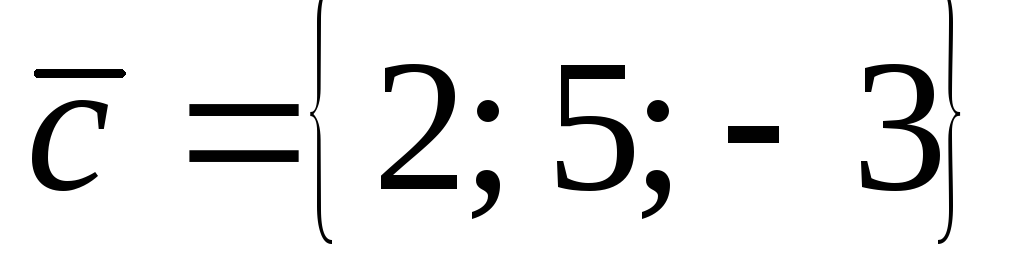 .
Найти орты векторов:
.
Найти орты векторов:-
 ;
2)
;
2)
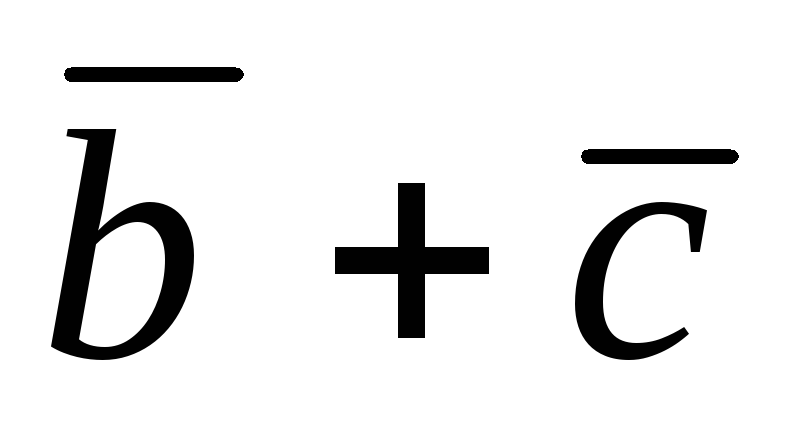 ;
3)
;
3)
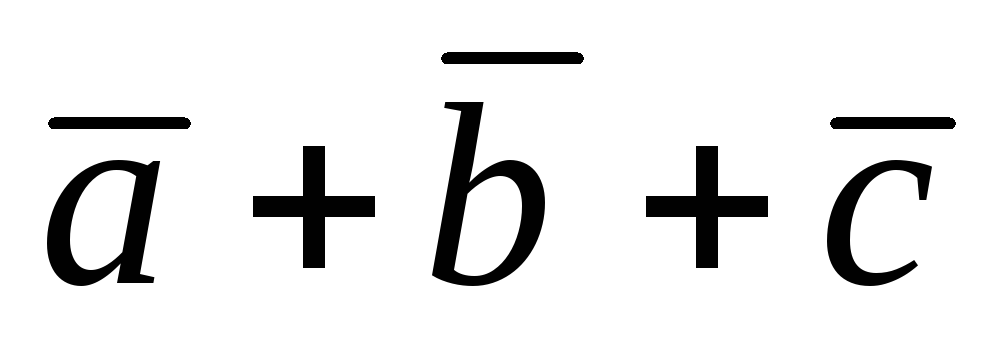 ;
4)
;
4)
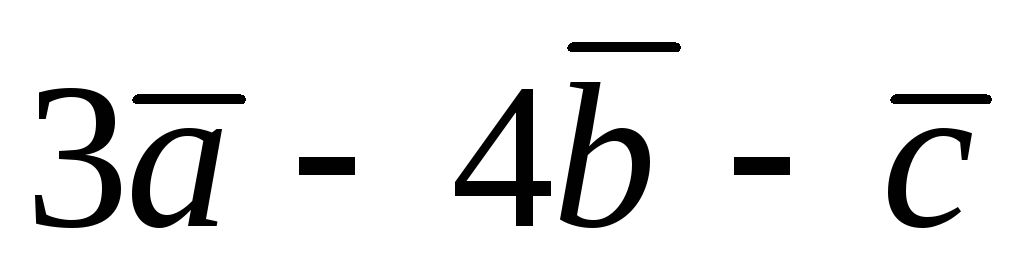 .
.
-
Ответ: 1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() .
.
-
Найти координаты вектора
 ,
направляющие косинусы которого равны
,
направляющие косинусы которого равны
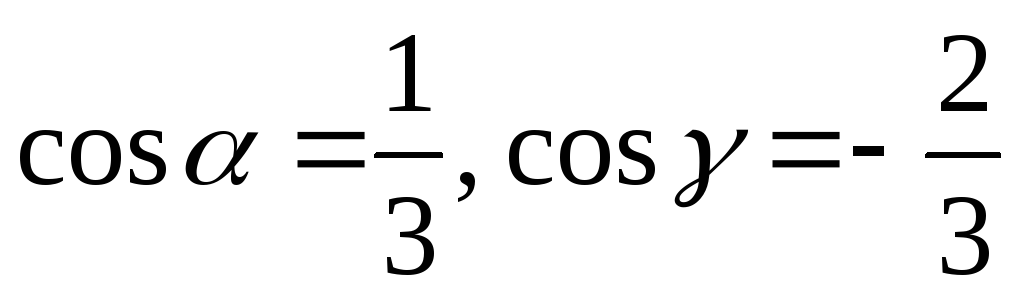 ,
если он образует с ортом
,
если он образует с ортом
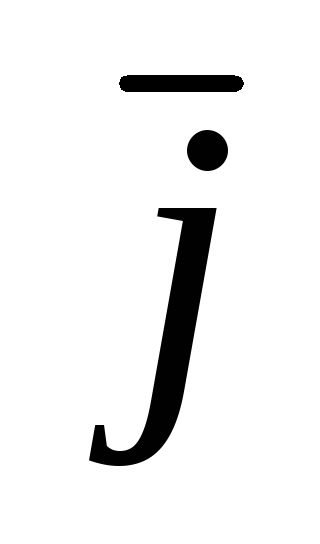 острый угол и имеет длину
острый угол и имеет длину
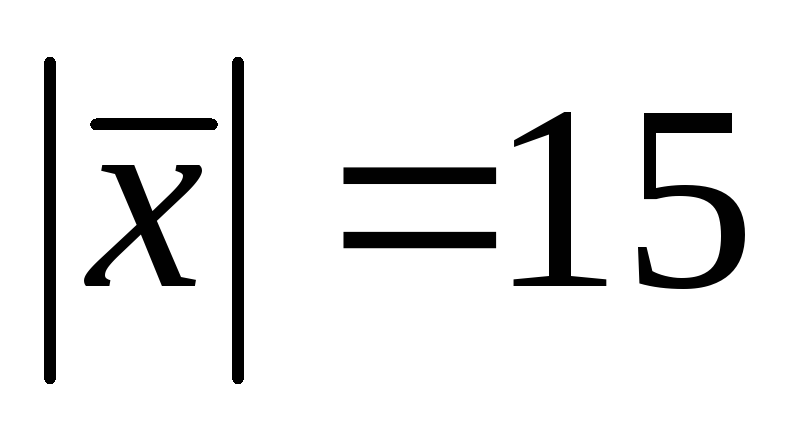 .
Ответ:
.
Ответ:
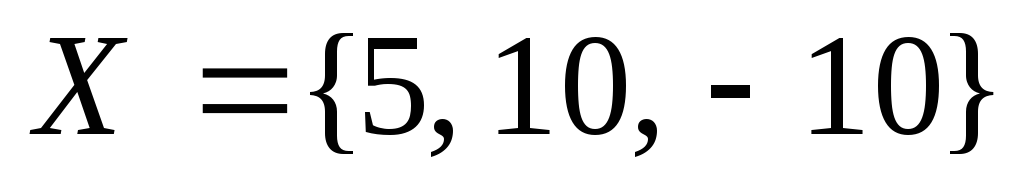
-
Три некомпланарных вектора
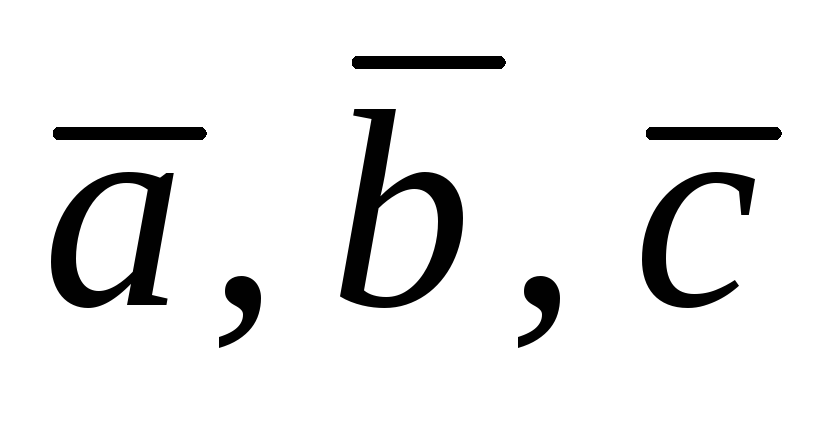 попарно ортогональны, а их длины
соответственно равны 2, 3, 6. Найти длину
вектора
попарно ортогональны, а их длины
соответственно равны 2, 3, 6. Найти длину
вектора
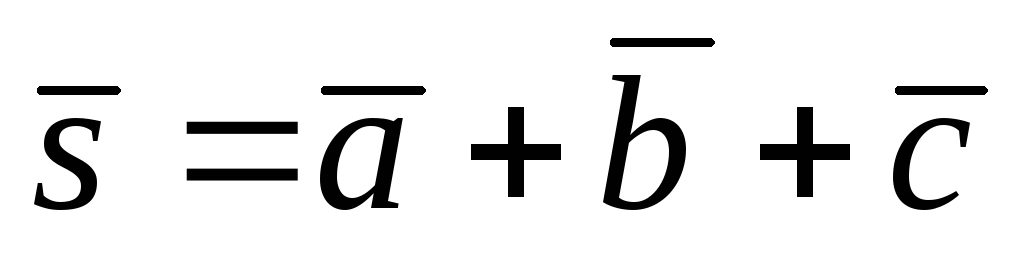 и направляющие косинусы этого вектора
в ПДСК, связанной с векторами
и направляющие косинусы этого вектора
в ПДСК, связанной с векторами
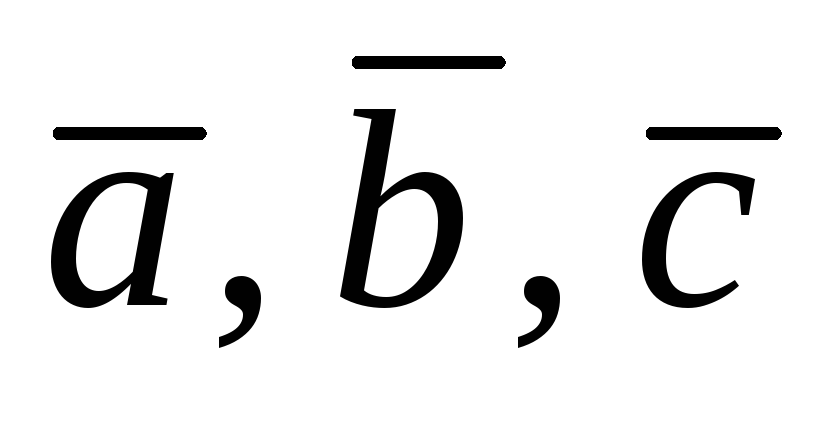 .
.
Ответ:
![]()
-
Дан куб ABCDA1B1C1D1 со стороной AB = 7. Точка T делит ребро DD1 в отношении 2:5, а точка S делит ребро B1C1 в отношении 3:4. Найти длину отрезка TS.
Ответ:
![]()
-
В прямоугольном параллелепипеде
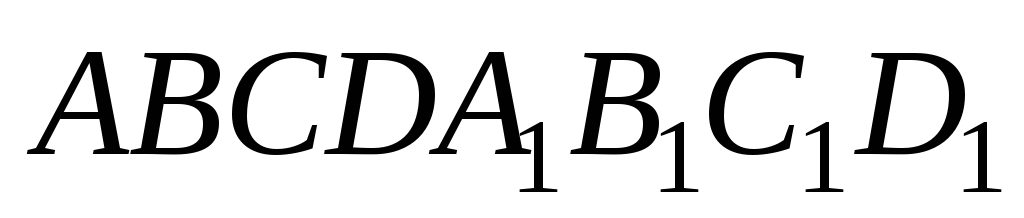 со сторонами
со сторонами
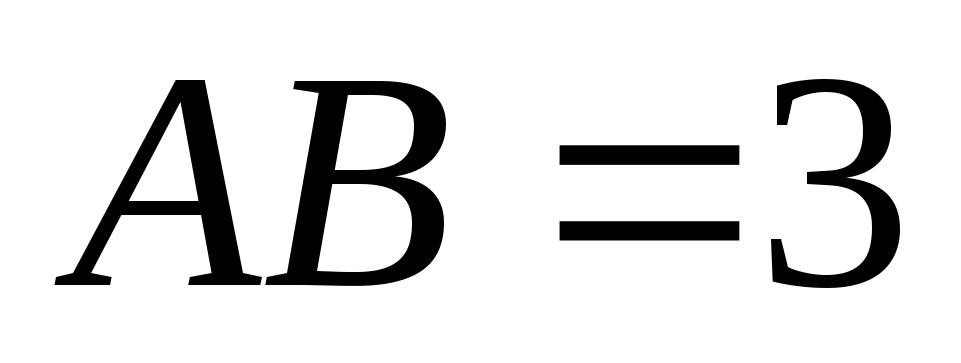 ,
,
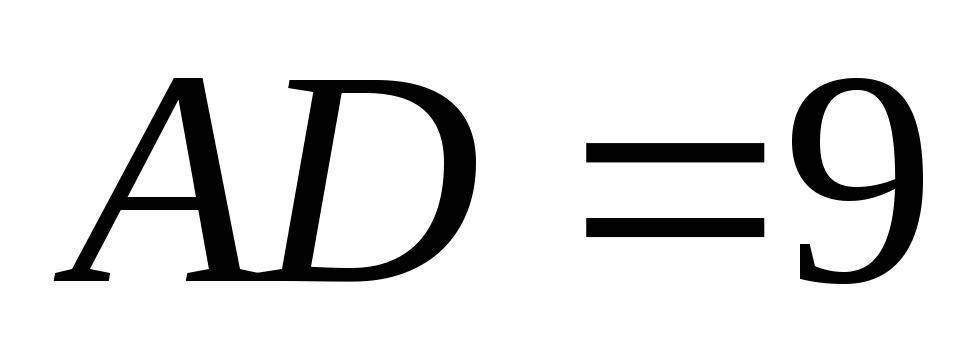 ,
,
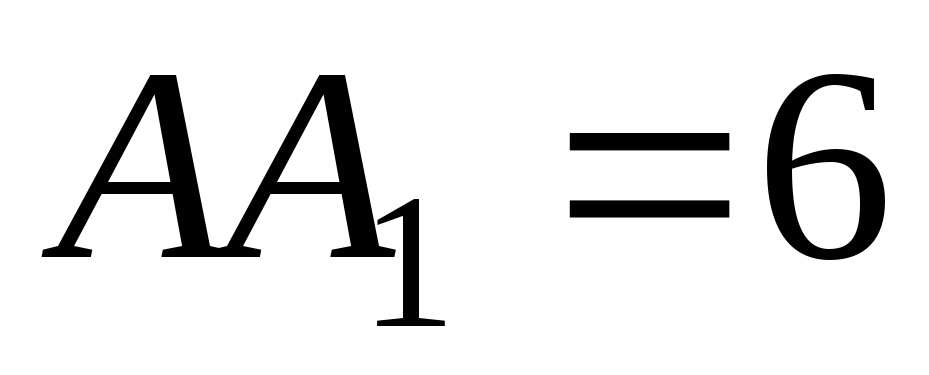 точка M
делит отрезок AC1
в отношении 2:1, точка N
ребро BB1
– в отношении 5:1, точка Q
делит отрезок
D1C
в отношении 2:1.
Найти:
точка M
делит отрезок AC1
в отношении 2:1, точка N
ребро BB1
– в отношении 5:1, точка Q
делит отрезок
D1C
в отношении 2:1.
Найти:
-
расстояние между точками N и Q;
-
расстояние от точки M до плоскости ВВ1С1С.
Ответ:
![]()
Самостоятельная работа
-
Даны три вектора
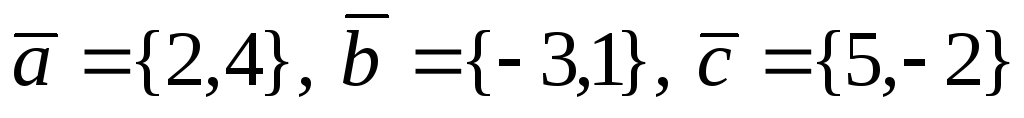 .
Найти векторы
.
Найти векторы
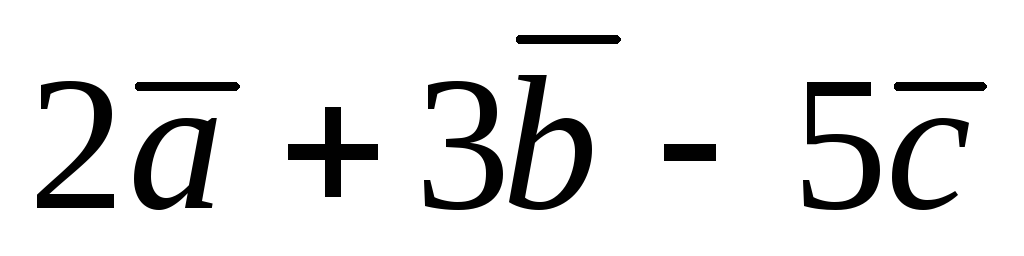 и
и
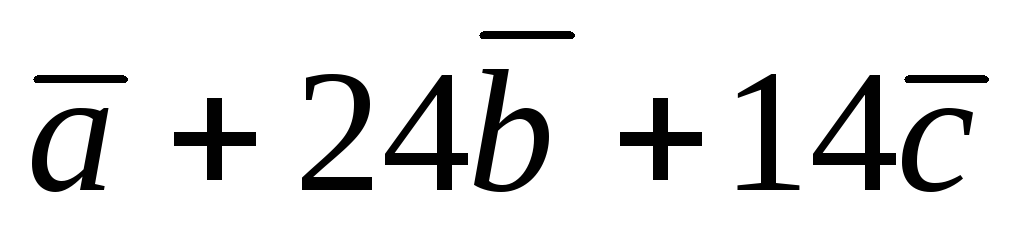 .
(1184)
.
(1184)
Ответ:
![]()
-
Даны три вектора
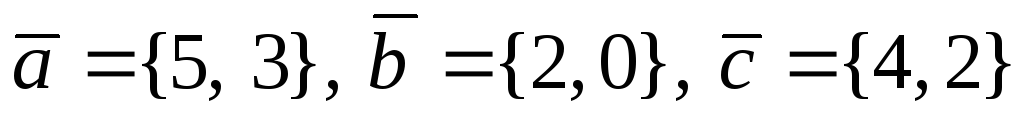 .
Подобрать числа
.
Подобрать числа
 и
и
 так, чтобы три вектора
так, чтобы три вектора
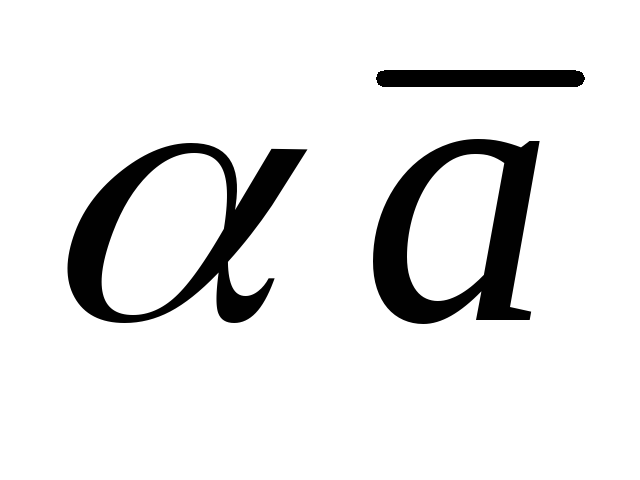 ,
,
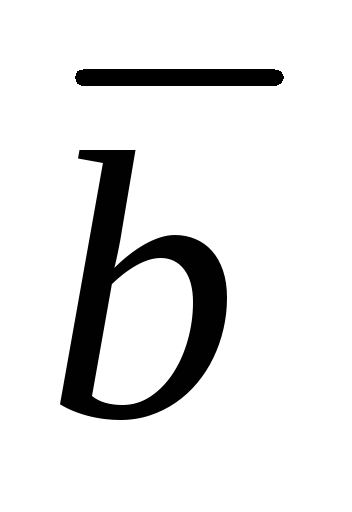 и
и
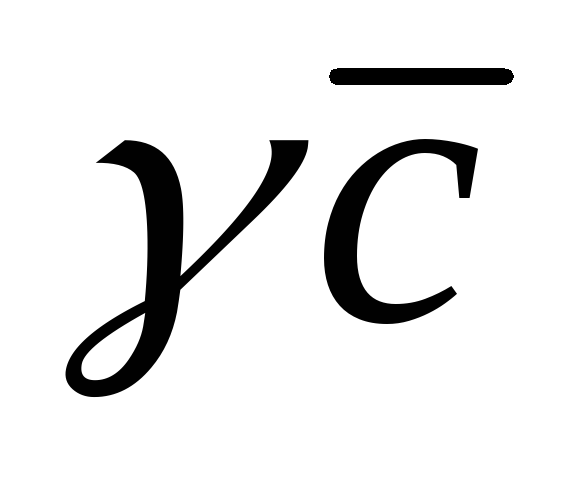 составили треугольник, если начало
вектора
составили треугольник, если начало
вектора
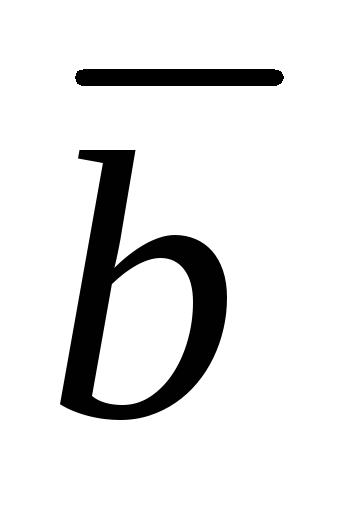 совместить с концом вектора
совместить с концом вектора
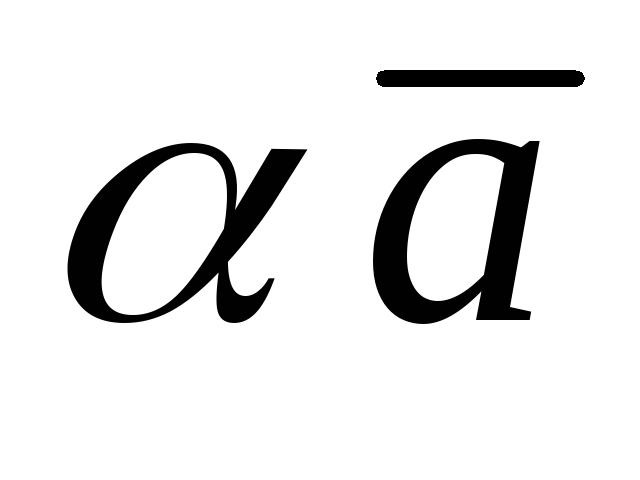 ,
а начало вектора
,
а начало вектора
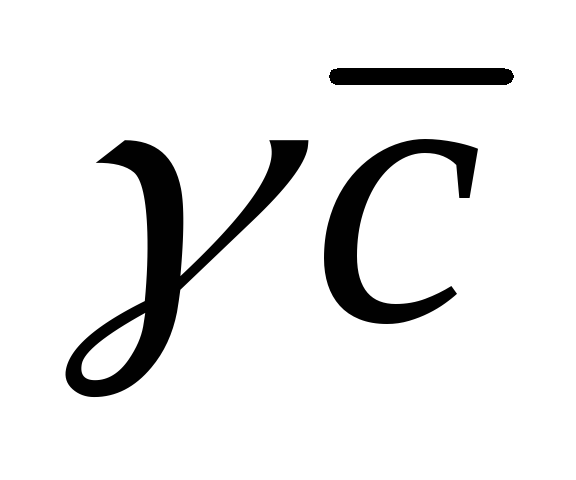 с концом вектора
с концом вектора
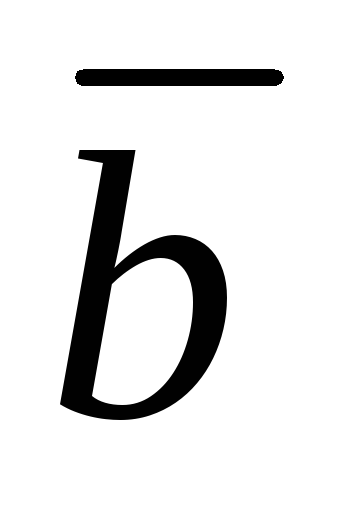 .
(1185)
.
(1185)
Ответ:
![]()
-
Из одной точки проведены векторы
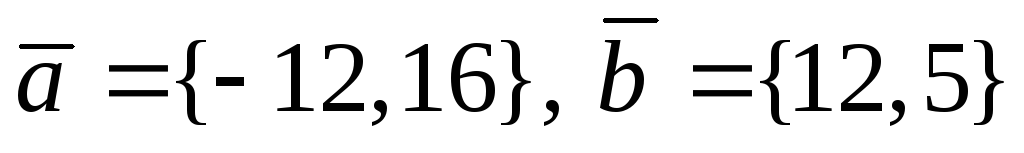 .
Найти координаты единичного вектора,
который, будучи проведен из той же
точки, делил бы угол между
.
Найти координаты единичного вектора,
который, будучи проведен из той же
точки, делил бы угол между
 и
и
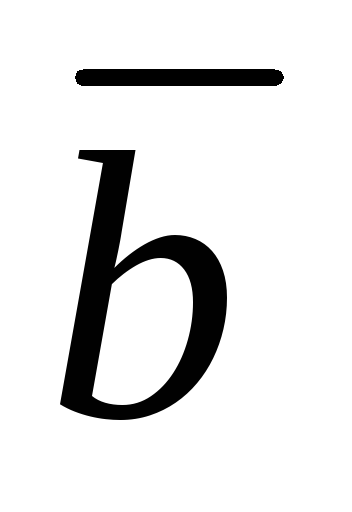 пополам. (1188)
пополам. (1188)
Ответ:
![]()
-
Даны три вектора
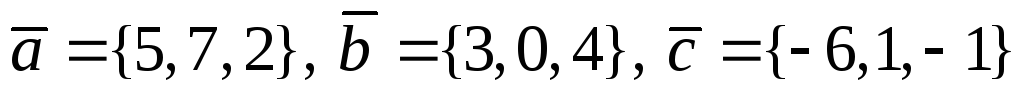 .
Найти векторы
.
Найти векторы
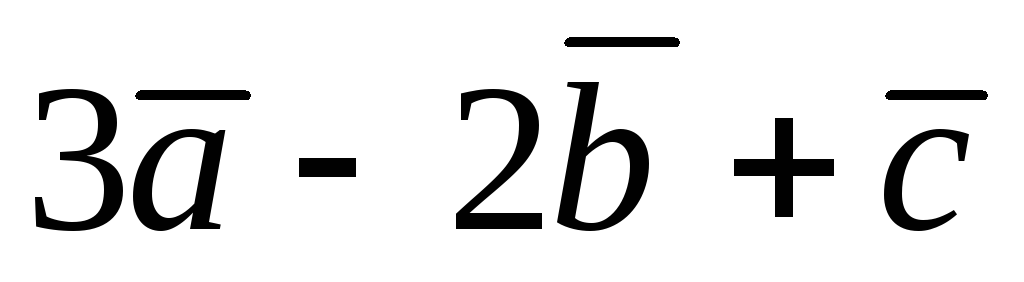 и
и
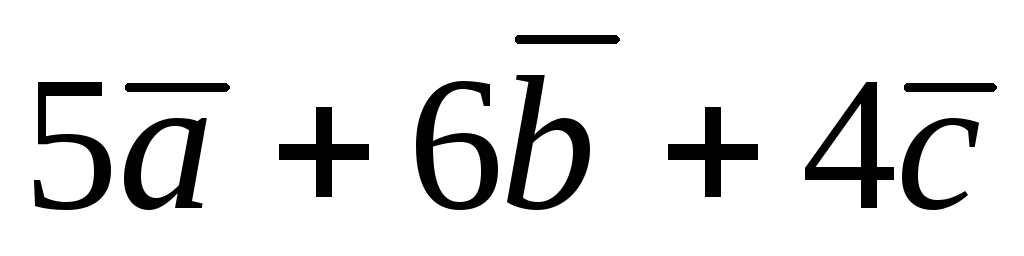 .
(1190)
.
(1190)
Ответ:
![]()
-
Относительно ортонормированного базиса дан вектор
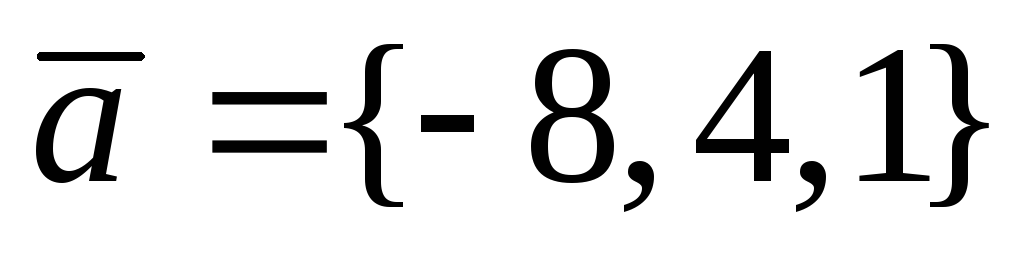 .
Найти единичный вектор, имеющий то же
направление, что и вектор
.
Найти единичный вектор, имеющий то же
направление, что и вектор
 .
(1195)
.
(1195)
Ответ:
![]()
