
АГ Векторная алгебра 2015-16 / Практическое занятие 4+СР(скалярное произведение)
.docПрактическое занятие № 4
(Скалярное произведение)
-
Векторы
 и
и
 образуют угол
образуют угол
 .
Зная, что
.
Зная, что
 ,
,
 ,
вычислить
,
вычислить
 .
Ответ: 242
.
Ответ: 242 -
В треугольнике АВС проведены медианы AD, BE и CF. Вычислить
 .
Ответ: 0
.
Ответ: 0 -
Найдите косинус угла между векторами
 и
и
 ,
если известно, что
,
если известно, что
 ,
а угол
,
а угол
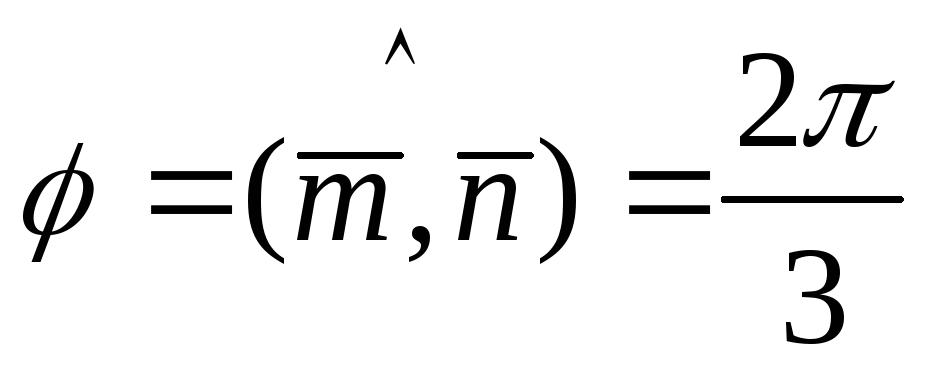 .
Ответ:
.
Ответ:

-
Дан прямоугольник ABCD и точка М (которая может лежать как в плоскости прямоугольника, так и вне её). Показать, что:
-
скалярное произведение векторов, идущих от точки М к двум несмежным вершинам прямоугольника, равно скалярному произведению векторов, идущих от той же точки к двум другим вершинам
 ∙
∙ =
= ∙
∙ .
. -
сумма квадратов векторов одной пары равна сумме квадратов другой пары (
 +
+ =
= +
+ ).
).
-
Даны три вектора.
 ,
,
 ,
,
 .
Вычислить выражения:
.
Вычислить выражения:
-
 . Ответ:
716
. Ответ:
716
-
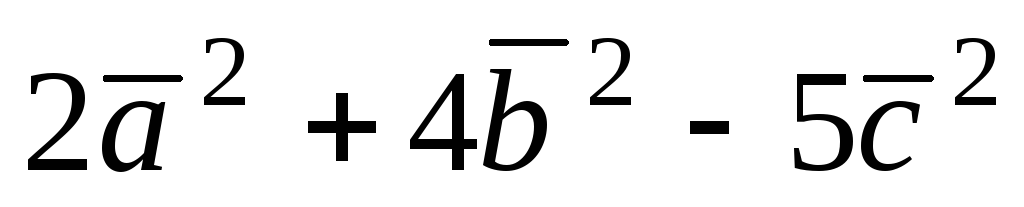 . Ответ:
-721
. Ответ:
-721 -
 . Ответ:
-353
. Ответ:
-353
-
Определить угол α между векторами
 и
и
 ,
заданными своими координатами в каждом
из случаев:
,
заданными своими координатами в каждом
из случаев:
-
 ,
,
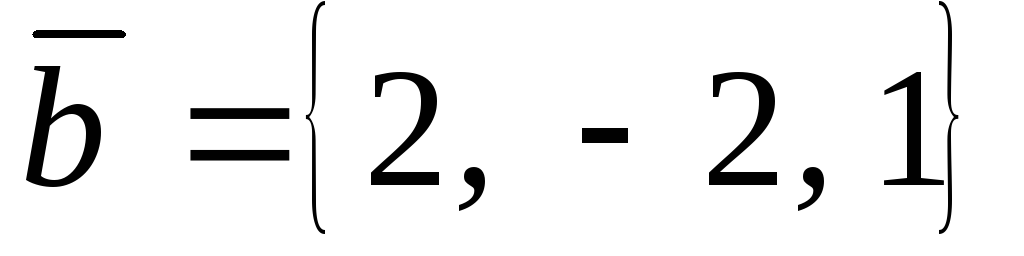 ;
Ответ:
;
Ответ:
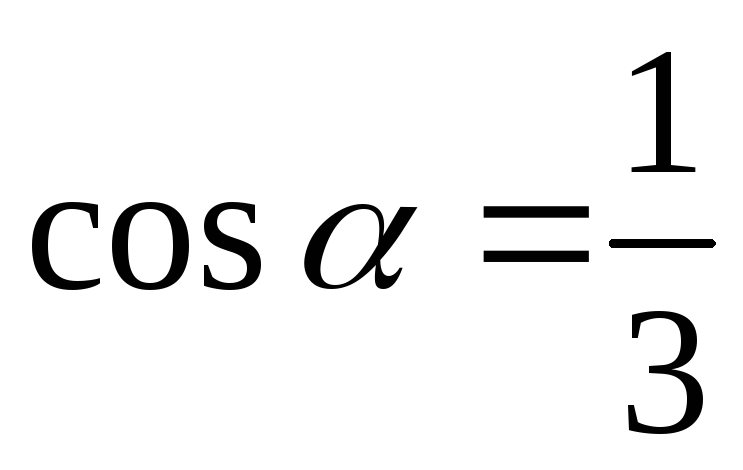
-
 ,
,
 .
Ответ:
.
Ответ:

-
Даны вершины треугольника А(2, 3, –1), В(4, 1, –2) и С(1, 0, 2). Найти:
-
внутренний угол при вершине С; Ответ:

-
 .
Ответ:
.
Ответ:

-
Дана правильная четырехугольная пирамида
 ,
сторона квадрата
,
сторона квадрата
 равна
равна
 ,
высота пирамиды равна 6. Точка K
делит ребро CS
в отношении 1:2,
точка L
делит AB
в отношении 3:1.
Найти
,
высота пирамиды равна 6. Точка K
делит ребро CS
в отношении 1:2,
точка L
делит AB
в отношении 3:1.
Найти
-
косинус угла между векторами
 и
и
 ; Ответ:
; Ответ:

-
проекцию вектора
 на направление вектора
на направление вектора
 . Ответ:
. Ответ:

Задания для самостоятельной работы по теме
«Скалярное произведение векторов. Проекция вектора на ось»
-
Зная, что
 ,
,
 ,
,
 ,
,
 ,
вычислить
,
вычислить
 .
.
Ответ: -13
-
Вычислить скалярное произведение двух векторов
 ,
зная их разложение по трём единичным
взаимно перпендикулярным векторам
,
зная их разложение по трём единичным
взаимно перпендикулярным векторам
 ,
,
 и
и
 :
:
 ,
,
 .
Ответ: 9
.
Ответ: 9
-
Дано:
 ,
,
 ,
,
 .
Найти модуль вектора
.
Найти модуль вектора
 .
.
Ответ:
![]()
-
Вычислить длину диагоналей параллелограмма, построенного на векторах
 ,
,
 ,
если известно, что
,
если известно, что
 ,
,
 ,
,
 .
.
Ответ: 15 и
![]()
-
Какой угол образуют единичные векторы
 и
и
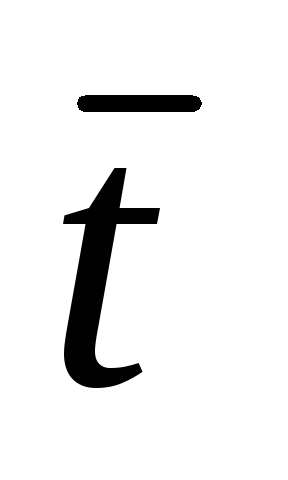 ,
если известно, что векторы
,
если известно, что векторы
 и
и
 взаимно перпендикулярны? Ответ:
взаимно перпендикулярны? Ответ:

-
Найти проекцию вектора
 на ось, имеющую направление вектора
на ось, имеющую направление вектора
 ,
где
,
где
 и
и
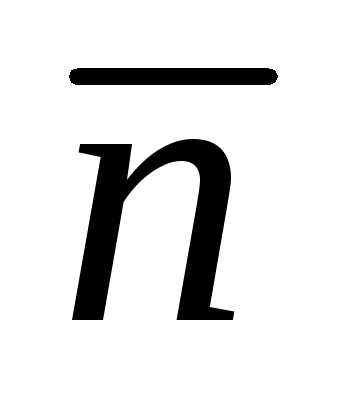 – взаимно перпендикулярные орты.
Вычислить углы между осью проекций и
единичными векторами
– взаимно перпендикулярные орты.
Вычислить углы между осью проекций и
единичными векторами
 и
и
 .
.
Ответ:
![]()
-
Доказать, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы.
-
Даны три вектора.
 ,
,
 ,
,
 .
Найти:
.
Найти:-
 ;
Ответ:
;
Ответ:

-
 ;
Ответ:
;
Ответ:

-
 .
Ответ:
.
Ответ:

-
-
Найти численную величину проекции вектора
 на ось, параллельную вектору
на ось, параллельную вектору
 .
Ответ: 3
.
Ответ: 3
-
Проверить, могут ли векторы
 ,
,
 быть рёбрами куба. Найти третье ребро
куба. Ответ:
быть рёбрами куба. Найти третье ребро
куба. Ответ:

-
Найти
 ,
зная, что
,
зная, что
 ,
,
 ,
,
 ,
,
 ,
проекция вектора
,
проекция вектора
 на вектор
на вектор
 равна 1. Ответ:
равна 1. Ответ:

-
Даны векторы
 ,
,
 ,
,
 .
Найти
.
Найти
 .
.
Ответ: 3
