
АГ Векторная алгебра 2015-16 / Практическое занятие 5+СР(векторное произведение)
.docПрактическое занятие № 5
по теме «Векторное произведение»
-
Даны два вектора
 и
и
 ,
для которых
,
для которых
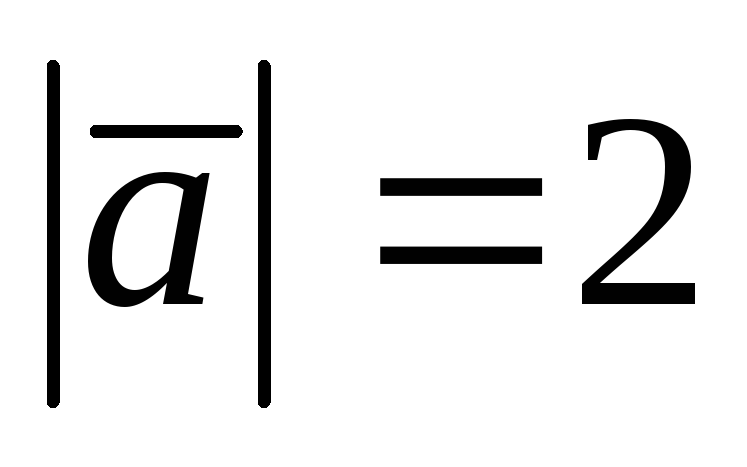 ,
,
 ,
,
 .
Найти
.
Найти
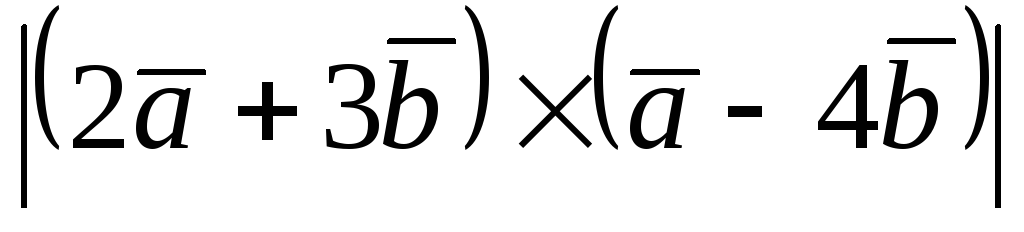 .
. -
Разложить вектор
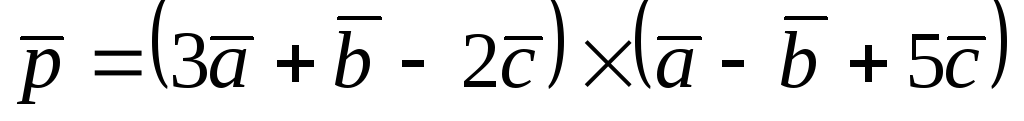 по взаимно перпендикулярным ортам
по взаимно перпендикулярным ортам
 ,
,
 и
и
 ,
образующим правую тройку.
,
образующим правую тройку. -
Векторы
 ,
,
 и
и
 удовлетворяют условию
удовлетворяют условию
 .
Доказать, что
.
Доказать, что
 .
. -
Показать, что если векторы
 ,
,
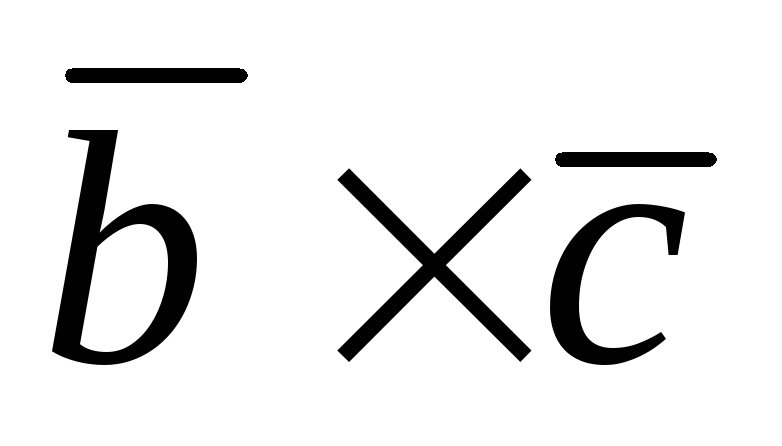 ,
,
 компланарны, то они и коллинеарны.
компланарны, то они и коллинеарны. -
Вычислить площадь параллелограмма, построенного на векторах
 и
и
 ,
где
,
где
 и
и
 ,
,
 .
. -
Найти координаты вектора
 ,
если
,
если
 ,
,
 .
. -
Даны вершины треугольника А(1, –1, 2), В(5, –6, 2) и С(1, 3, –1). Найти длину его высоты, опущенной из вершины В на сторону АС.
-
Дан куб АВСDA1B1C1D1 с ребром единичной длины,
 ,
,
 ,
,
 .
Найти площадь треугольника MNP
и расстояние от точки P
до прямой MN.
.
Найти площадь треугольника MNP
и расстояние от точки P
до прямой MN. -
Даны векторы
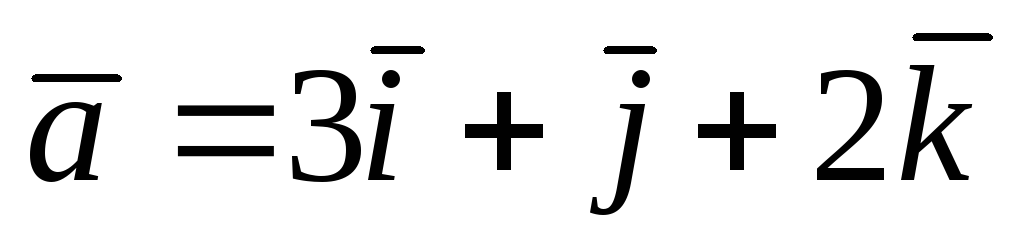 ,
,
 и
и
 .
Найти
.
Найти
 и
и
 .
.
Задания для самостоятельной работы № 5
по теме «Векторное произведение»
-
Показать, что
 .
Выяснить геометрический смысл этого
равенства.
.
Выяснить геометрический смысл этого
равенства. -
Дан вектор
 ,
где
,
где
 ,
,
 и
и
 – взаимно перпендикулярные орты,
образующие левую тройку. Вычислить его
длину.
– взаимно перпендикулярные орты,
образующие левую тройку. Вычислить его
длину. -
Векторы
 и
и
 образуют угол 450.
Найти площадь треугольника, построенного
на векторах
образуют угол 450.
Найти площадь треугольника, построенного
на векторах
 и
и
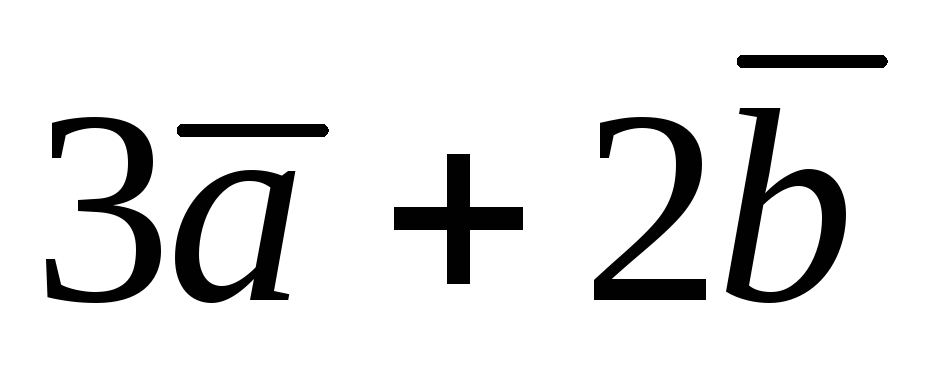 ,
если
,
если
 .
. -
Вычислить проекцию вектора
 на ось, имеющую направление вектора
на ось, имеющую направление вектора
 ,
где
,
где
 ,
,
 и
и
 – взаимно перпендикулярные орты.
– взаимно перпендикулярные орты. -
Даны векторы
 ,
,
 .
Найти
.
Найти
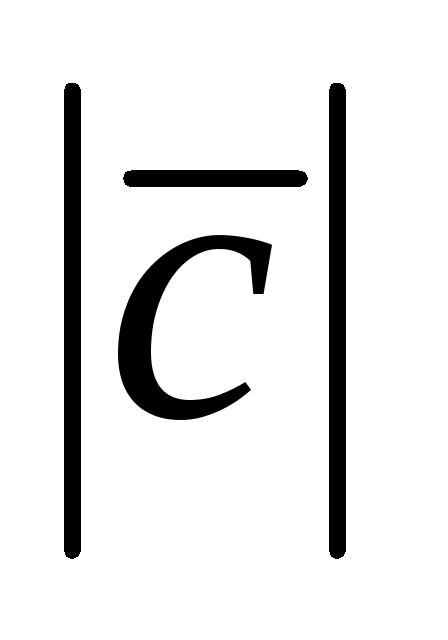 ,
если
,
если
 .
. -
Вычислить синус угла, образованного векторами
 и
и
 .
. -
Найти площадь треугольника, построенного на векторах
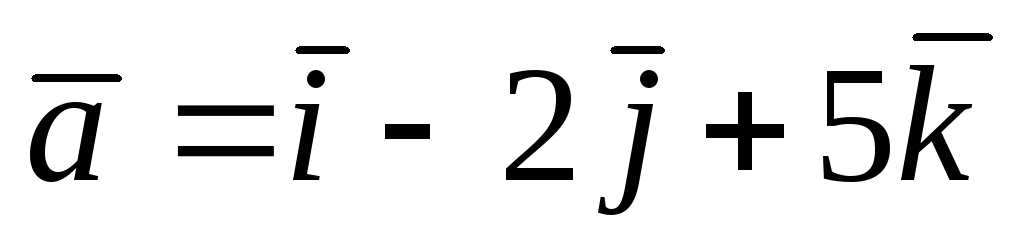 и
и
 .
. -
В кубе с ребром единичной длины АВСDA1B1C1D1 точки M, N, P и Q заданы равенствами
 ,
,
 ,
,
 ,
,
 .
Найти
.
Найти
 .
. -
В тетраэдре ABCD все плоские углы при вершине D равны 900, DA=2, DB=4, DC=6. Точки K, L и P лежат на отрезках
 ,ВС
и DC
соответственно и удовлетворяют условиям:
,ВС
и DC
соответственно и удовлетворяют условиям:
 ,
,
 ,
,
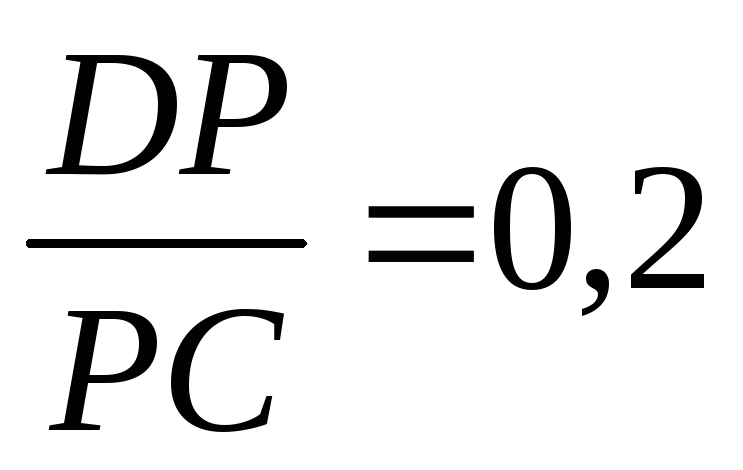 .
.
Найти:
-
синус внутреннего угла при вершине P в треугольнике KPL;
-
высоту треугольника KPL, опущенную на сторону KP.
