АГ Векторная алгебра 2015-16 / Практическое занятие 6 (Смешанное произведение)

Практическое занятие № 6 по теме «Смешанное произведение»

1. Вычислить произведение

.

2. Вычислить произведение 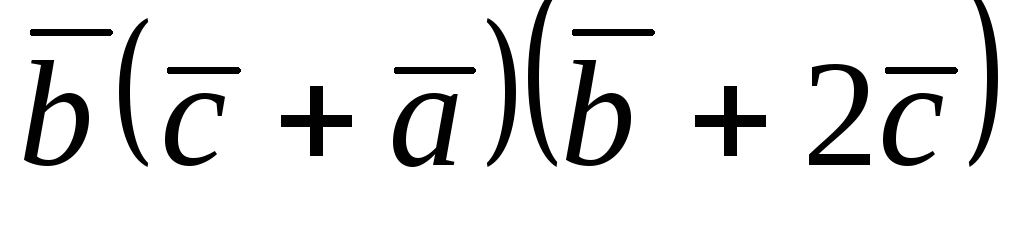, если .

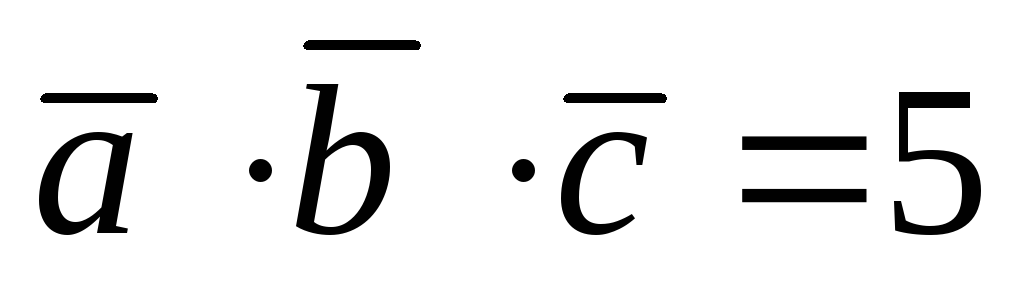3. Проверить, компланарны ли данные векторы, если , и – взаимно перпендикулярные орты:

1. ,,;

2. ,, ;

3. , , .

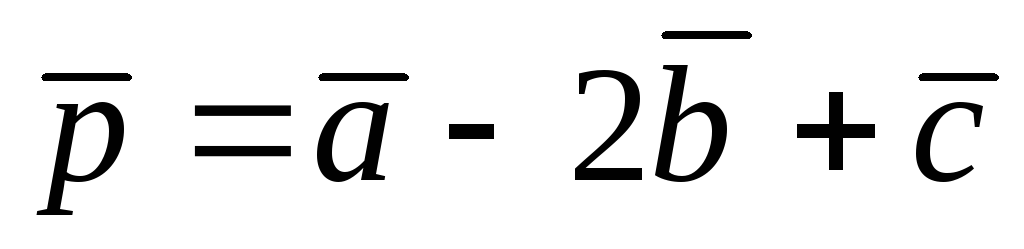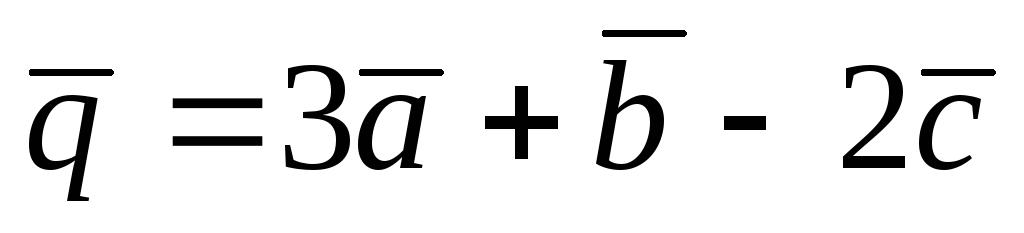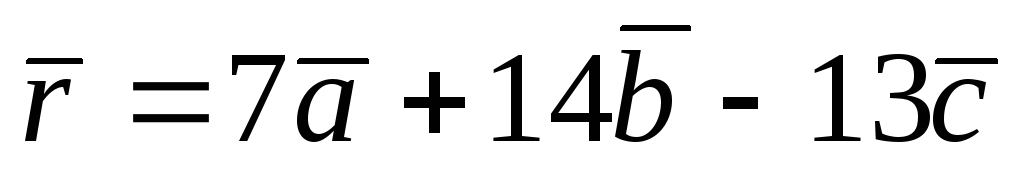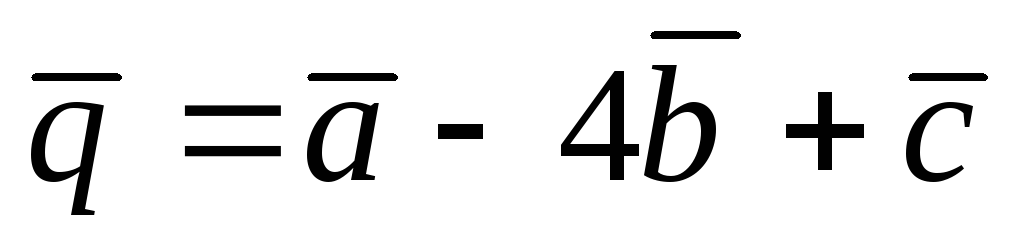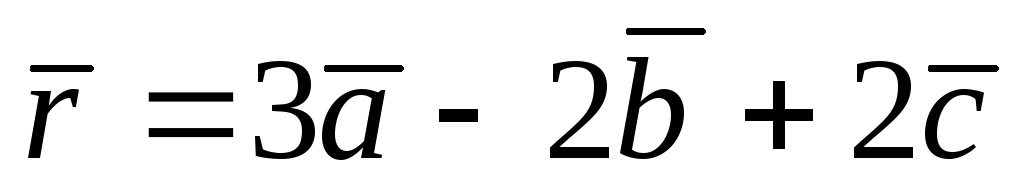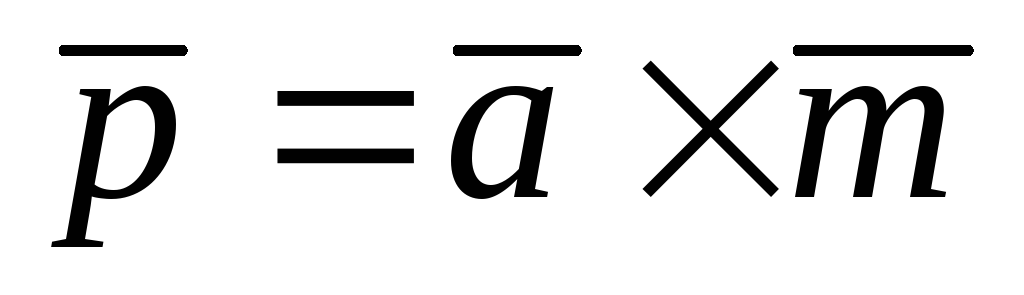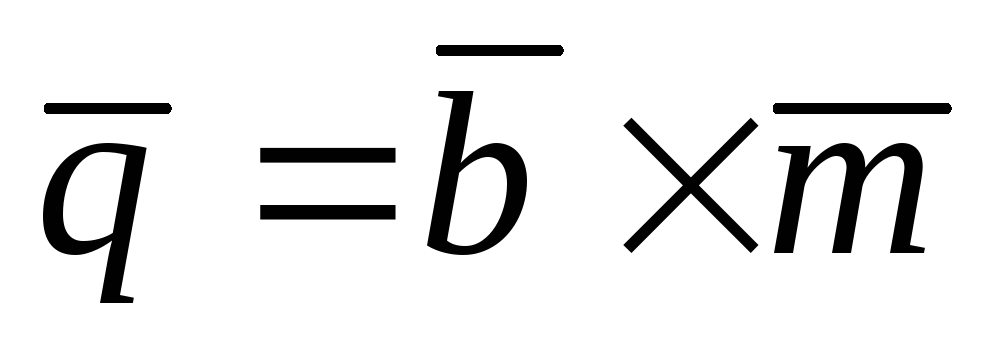4. При каком значении параметра λ векторы 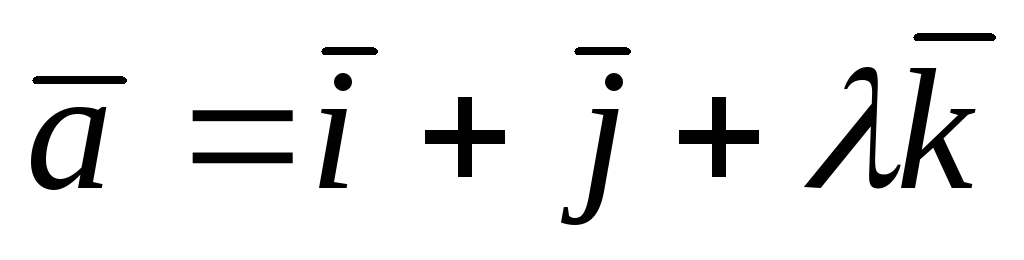, 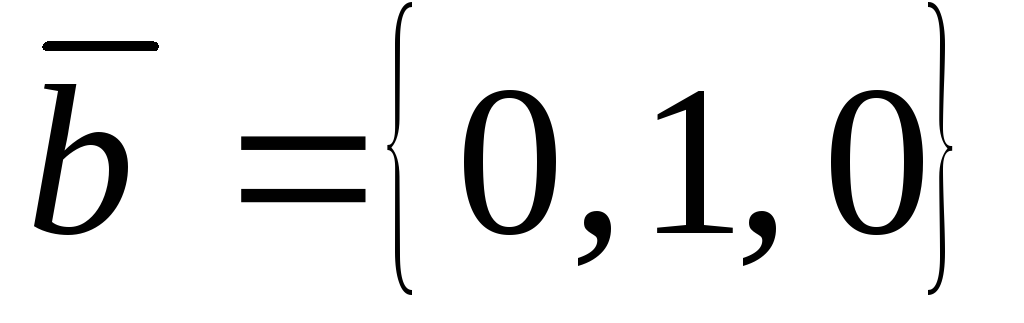и 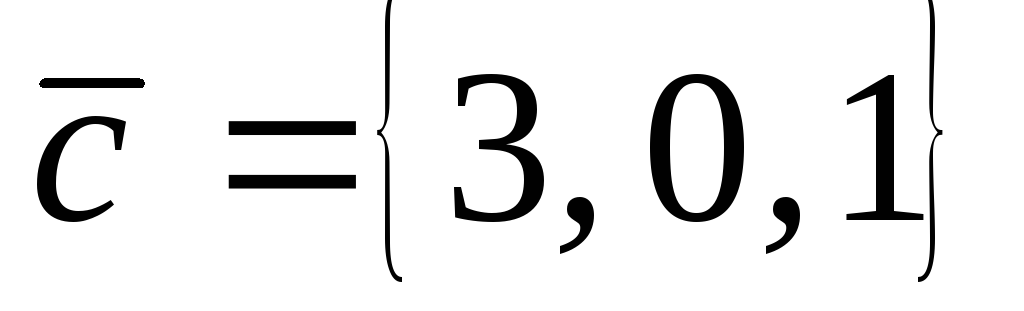компланарны?

5. Даны вершины пирамиды А(5, 1, –4), В(1, 2, –1), С(3, 3, –4), S(2, 2, 2). Найти длину высоты, опущенной из вершины S на грань АВС.

6. Объём тетраэдра равен 5, три его вершины находятся в точках А(2, 1, –1), В(3, 0, 1) и С(2, –1, 3). Найти координаты четвёртой вершины D, если известно, что она лежит на оси ординат.

7. АВСDA₁B₁C₁D₁ – параллелепипед объёма V. Точки M, N, P и Q заданы равенствами 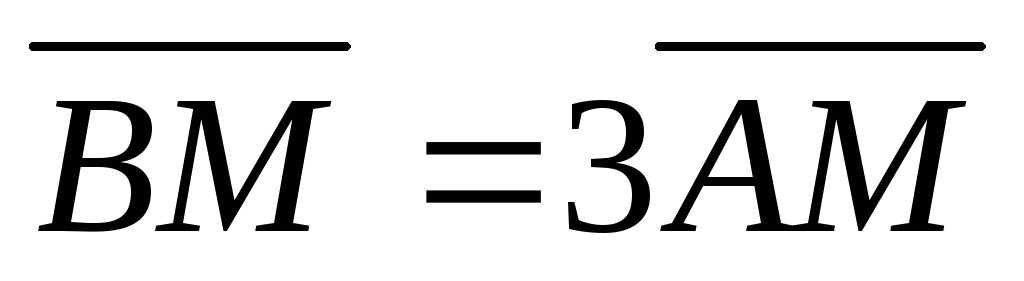, , 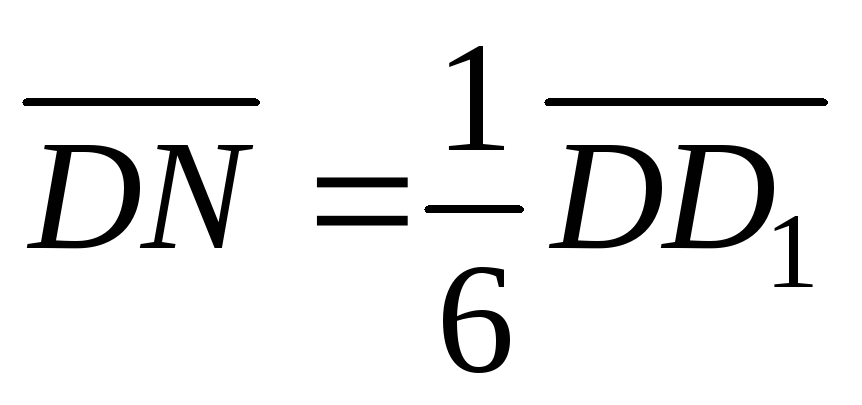, 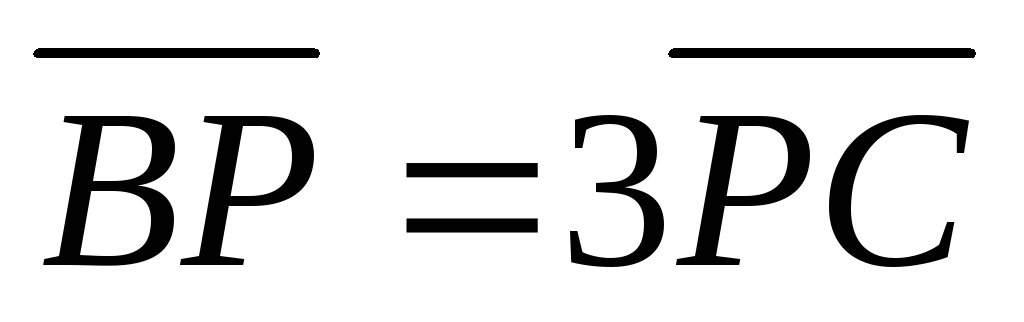. Найти объём тетраэдра MNPQ.

8. Дана пирамида с вершинами А₁(1, 2  3), А₂(–2, 4, 1), А₃(7, 6, 3) и А₄(4, –3, –1). Найти:

   1. длину рёбер А₁А₂, А₁А₃, А₁А₄;

   2. площадь грани А₁А₂А₃;

   3. угол между рёбрами А₁А₃ и А₁А₄;

   4. объём пирамиды;

   5. длину высоты, опущенной на грань А₁А₂А₃.