Глава 6. Практикум по ЧисленныМ методАм и математическоМу моделированиЮ

6.1. Введение

С развитием информационных технологий появляется все больше возможностей для исследования математических моделей с помощью численных методов. Кроме универсальных языков программирования, применяемых для решения математических задач, существует множество специализированных математических пакетов программ, в основе которых лежат уже готовые алгоритмы вычислений с использованием численных методов. К их числу относятся MathCAD, Maple, MathLAB, Mathematica.

Например, при использовании системы MathCAD, по сравнению с универсальными языками программирования, облегчается графическое представление результатов, упрощаются промежуточные вычисления. Кроме того, в системе MathCAD с целью освоения алгоритмов численных методов их можно реализовать средствами программирования, а затем проверить результат с помощью встроенных процедур и функций.

Другим программным продуктом, с помощью которого можно производить численные расчеты, является табличный процессор Excel. В нем реализован принцип табличных вычислений и при изучении численных методов этот принцип существенно помогает при организации расчетов, чему способствует наглядное представление промежуточных результатов. Так как табличный процессор EXEL имеет большую популярность и его изучение предусмотрено в школьной программе, то описанию работы с этим программным продуктом будет уделено меньше внимания, чем системе MathCAD.

Табличные результаты приведенных примеров в основном вычислены с помощью программы EXEL. Данное пособие подразумевает значительную самостоятельную работу студентов, поэтому, как правило, в этих примерах чаще даннно табличное представление результатов вычислений, без отображения формул.

В пособии приведена краткая справка по компьютерной системе MathCAD, а также предлагается множество примеров с использованием этой системы. Приводятся стандартные функции для вычислений. Во многих случаях математическая запись формул совпадает с формой записи, принятой в MathCAD, что облегчит студентам переход к самостоятельной практической работе с этим программным продуктом.

6.2. Основные правила работы с MathCad 13

После запуска системы в левом верхнем угле рабочего поля программы появляется курсор «+». При необходимости его можно установить в другое место рабочего поля с помощью стрелок или мыши. Простейшие математические расчеты можно производить практически сразу.

Для построения сложных математических выражений, вывода результатов в графическом виде, программирования и т.д. используется панель инструментов Math (математика). Если она не отображена на экране, то ее можно восстановить, используя пункты верхнего меню View  Toolbars Math.

С помощью каждого инструмента на данной панели можно вызвать соответствующую ему панель со своим набором инструментов. Так, после выбора инструмента Calculator (калькулятор) появляется соответствующая ему панель. Чтобы набрать дробь, например 3/23, необходимо сначала набрать числитель «3», выбрать с помощью мыши инструмент и набрать знаменатель «23». Для получения результата необходимо нажать клавишу «=».

При построении выражений часто требуется выделить ту или иную его часть. В этом случае используют клавишу «пробел». В предыдущем случае, если необходимо продолжить выражение, но уже не в знаменателе, необходимо нажать «пробел» один раз. Чтобы выделить все выражение, «пробел» нажимают столько раз, сколько это необходимо для полного выделения.

Для построения дроби вместо выбора инструмента на панели можно было воспользоваться клавишей « / ». Ниже приводятся горячие клавиши для других операций, дублируемых набором на клавиатуре.

Отображение в документе	Набор на клавиатуре	Отображение в документе	Набор на клавиатуре
:=	:		X \
…	;		X [Ctrl + \]
∙	*	|X|	| X
	3 / 24	N!	! N
Z2	Z^2		t ? A(t)
X1	X[1	Вставить матрицу	Ctrl+M

Формат отображения числовых значений результата (например, с фиксированной точкой или экспоненциальный) может быть выбран с помощью диалогового окна Result Format (формат результата). Это окно можно открыть через пункт верхнего меню Format, в котором выбирается подпункт Result.

Работа с функциями. Для работы с функциями используется обычная математическая запись, отличие только в том, что выражение функции не приравнивается, а присваивается. Например, . Такая запись представляет собой описание функции. Чтобы вычислить функцию для определенного значения аргумента, нужно поставить курсор ниже описания функции, написать имя функции с необходимым аргументом в скобках, после чего нажать клавишу «=». Для того чтобы найти корни функции, необходимо воспользоваться встроенной функциейsolve. Проще всего в нашем случае ниже выражения для функции набрать f(x), а затем выбрать в меню Math  Symbolic функцию solve. В предлагаемом поле следует ввести аргумент х и нажать «Enter». После всех перечисленных действий на рабочем поле будет отображено следующее:

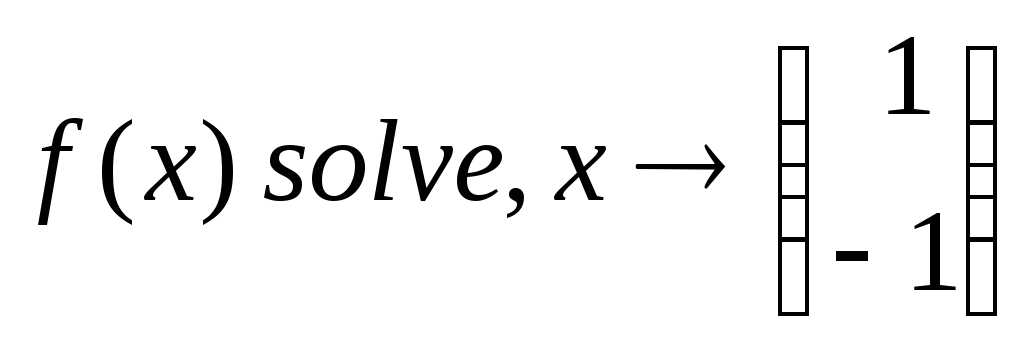
Построение графиков. Чтобы построить график функции в декартовых координатах нужно установить курсор ниже введенного выражения и воспользоваться инструментом на панелиGraph(графика).

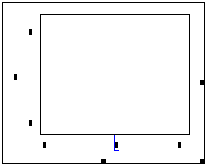
После этого на месте курсора отобразится шаблон для построения графика. В этом шаблоне располагаются пустые поля, предназначенные для ввода данных (черные прямоугольники на рисунке слева).

Если в крайнем левом прямоугольнике набрать f(x) и нажать клавишу «Enter», то график будет построен автоматически с параметрами по осям, определенными самой системой. При необходимости параметры осей легко меняются, если щелкнуть левой клавишей мыши по выбранному элементу.

Так же можно менять свойства графика, используя контекстное меню. Для этого нужно щелкнуть правой клавишей мыши по рисунку и выбрать пункт Format.

На одном графике можно построить две и более функций. В этом случае выше графика отдельно записываются выражения для функций, а затем в крайнем левом поле графика через запятую вводятся их наименования с переменными аргументами (например, f(x), h(x)). При вводе запятой курсор автоматически переходит на новую строку.

Дифференцирование и интегрирование в системе MathCAD так же производятся достаточно простым способом, однако имеются моменты, которые необходимо отметить. Шаблон оператора дифференцирования не должен конструироваться как дробь, он вводится либо с помощью горячих клавиш (см. таблицу выше), либо с помощью инструментана панелиCalculus (исчисление). Результату интегрирования или дифференцирования удобно ставить в соответствие свое имя функции с помощью операции присваивания. Например, . Для просмотра результата выражения сразу же после его ввода нужно воспользоваться инструментом(или жеCtrl+.), после чего нажать «Enter». Часто полученное выражение бывает громоздко и требует упрощения его вида, для этого используют функцию Simplify. Упрощаемое выражение сначала выделяется с помощью пробела, затем на панели Symbolic выбирается функция Simplify, в конце нажимается «Enter».

Работа с векторами и матрицами. При работе с векторами и матрицами используется панель операций с матрицами Matrix. Применение этих инструментов не столь очевидно, как, например, для инструментов арифметических операций, поэтому ниже они рассмотрены подробно.

задает матрицу или вектор (Ctrl+M)

- нижний индекс ( [ )

- вычисление обратной матрицы (можно просто записать x в -1 степени)

- вычисление определителя матрицы (можно вводить с помощью символа |)

- поэлементные операции с матрицами: если А={a_ij}, а B={b_ij}, то = {a_ij+b_ij} или = {a_ij·b_ij} (Ctrl + -)

- выбор столбца в матрицы: M^<j> – j-ый столбец матрицы (Ctrl+6)

- транспонирование матрицы (Ctrl+1)

- определение диапазона ( ; )

- вычисление произведения матриц, скалярного произведения

векторов (*)

- вычисление векторного произведения векторов (Ctrl+8)

- вычисление суммы элементов матрицы (Ctrl+4)

При работе с матрицами, можно производить операции как со всей матрицей, так и с ее отдельными элементами. Чтобы ввести матрицу А, необходимо набрать «А:», а затем выбрать инструмент, задающий матрицу . После выбора необходимого количества строк и столбцов можно вводить элементы матрицы. Ниже приведен пример вычисления определителя матрицы и ее произведения на вектор, а так же работы с ее отдельными элементами.

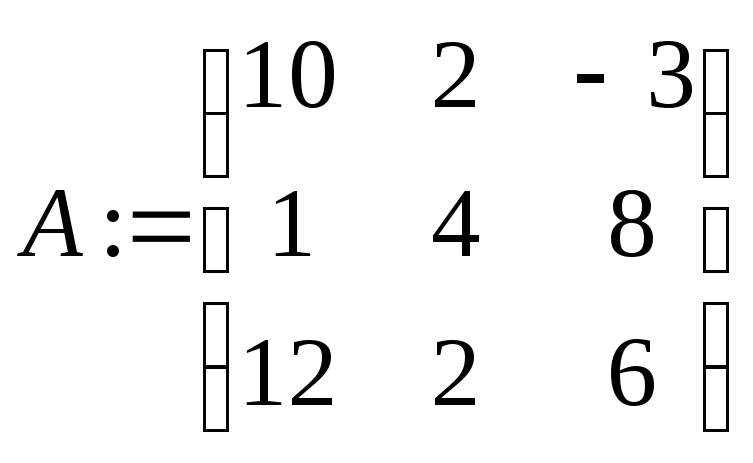
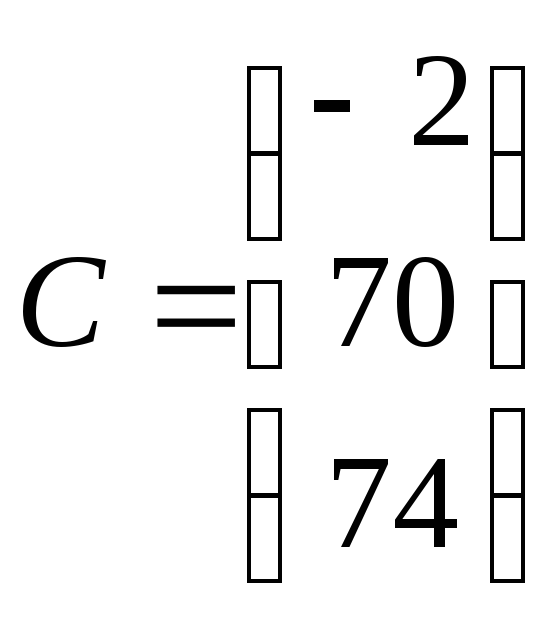
Заметим, что нумерация индексов матрицы по умолчанию начинается с нуля. Для того, чтобы начать нумерацию с единицы необходимо перед выводом результата набрать команду ORIGIN=1 (верхний регистр обязателен).

Для работы с матрицей используется множество встроенных функций, основные из них приводятся ниже.

max(A) – вычисление наибольшего элемента в матрице А;

min(А) – вычисление наименьшего элемента в матрице А;

tr(A) – вычисление следа (суммы диагональных элементов) квадратной матрицы А;

rows(A) – вычисление числа строк в матрице A;

cols(A) – вычисление числа столбцов в матрице А;

diag(v) – создание диагональной матрицы, элементы главной диагонали которой хранятся в векторе v;

identity(n) – создание единичной матрицы порядка n;

augment(A,B) – формирует матрицу, в первых столбцах которой содержится матрица А, а в последних – матрица B (матрицы А и В должны иметь одинаковое число строк);

stack(A,B) – формирует матрицу, в первых строках которой содержится матрица А, а в последних – матрица В (матрицы А и В должны иметь одинаковое число столбцов);

submatrix(A,ir,jr,ic,jc) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir по jr и в столбцах с ic по jc, ir<jr, ic<jc.

Программирование. Одной из наиболее сложных возможностей MathCAD является программирование. Инструменты программирования находятся на панели Programming.

Слева рассмотрен пример программы для суммирования n первых натуральных чисел. С помощью этой программы определяется функция f с переменным параметром n. Ниже программы в последней строке показано использование этой функции с параметром 5.

Для ввода этой программы после набора комбинации клавиш «f(n):» необходимо выбрать инструмент Add Line (можно использовать «]»).

После этого появляется специальный шаблон, в котором линия слева определяет границы оператора.

Внутри шаблона производится набор тела функции.

В программе использованы локальные переменные rez и i. Присваивание производится с помощью инструмента (который можно вводить символом «{» ). При использовании цикла по параметруfor был указан диапазон 1..n. Необходимо отметить, что при его наборе нельзя использовать обычные две точки, их вводят, например, горячей клавишей «;». Если бы внутри тела цикла было больше одной строки, то необходимо было бы снова использовать инструмент Add Line. Итоговое значение функции f задается командой return. В данном случае команду return можно было опустить.

В следующем примере используется цикл с предусловием while. Здесь определяется функция Summ_All, с помощью которой вычисляется сумма всех элементов матрицы. В этом же примере представлены результаты расчетов с помощью определенной функции для матрицы А и вектора B, с использованными ранее значениями.