
caplin_nikulin_modelirovanie_v_metallurgii
.pdf
dF = σ dx, |
(3.30) |
где σ, [Н/м] – коэффициент поверхностного натяжения жидкости. При постоянном коэффициенте поверхностного натяжения эта сила не является причиной движения жидкости, она лишь вызывает дополнительное давление, изменяя уровень жидкости в каналах малого диаметра (капиллярах), либо стремится придать конечному объему жидкости форму с наименьшей поверхностью. Например, в условиях невесомости жидкость принимает форму шара. Однако при переменном коэффициенте поверхностного натяжения силы поверхностного натяжения не скомпенсированы, появляется причина движения, и граничные условия на свободнойповерхности в этом случае принимают вид:
|
|
µ |
∂ u |
|
|
=∂σ |
. |
(3.31) |
|||
|
|
|
|
|
|
|
|||||
|
|
|
∂ y |
|
y =0 |
∂ |
x |
|
|||
|
|
|
|
|
|
|
|||||
Коэффициент поверхностного натяжения зависит от тем- |
|||||||||||
пературы |
|
|
|
|
|
|
|
|
|
|
|
σ |
(T )= σ −0 |
∂σ |
|
(T− |
T0=) σ |
+0γ −(T T0 ) , |
(3.32) |
||||
∂ T |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
где γ = −∂σ ∂ |
T [Н/(м·К)]– температурный коэффициент по- |
||||||||||
верхностного натяжения, отрицательное значение этого коэффициента отражает тот факт, что сила поверхностного натяжения уменьшается с увеличением температуры. С учетом линейной зависимости (3.32)
∂σ |
|
σd ∂ |
|
T |
∂ T |
||
∂ x |
= |
|
|
|
= γ∂ |
|
|
|
dT |
∂ x |
x |
||||
и граничное условие (3.31) принимает вид:
µ |
∂ u |
|
|
= γ |
∂ |
T |
|
|||
|
|
|
|
|
|
|
. |
(3.33) |
||
∂ y |
|
y =0 |
∂ |
x |
||||||
|
|
|
|
|
|
|
91 |
|||
|
|
|
|
|
|
|
|
|
|
|

Явление движения жидкости, инициированное силами поверхностного натяжения при неоднородном распределении температуры, называют термокапиллярным эффектом, а возникающую конвекцию – термокапиллярной конвекцией, или конвекцией Марангони.
|
|
Конвекция Марангони при- |
|
|
|
водит к появлению дополнитель- |
|
|
|
ных течений у поверхности жид- |
|
|
|
кости. Например, при плавлении |
|
|
|
металла концентрированным пуч- |
|
|
|
ком лазерной энергии пятно рас- |
|
Рис. 3.10. Схема конвекции |
плава «расползается», увеличива- |
||
ется в диаметре, превышая диа- |
|||
Марангони при плавлении |
метр пучка из-за термокапилляр- |
||
металла лазером |
ной конвекции (рис. 3.10). |
||
|
|
||
Система |
дифференциальных |
уравнений в совокупности |
|
с условиями |
однозначности |
дает |
математическую формули- |
ровку краевой задачи конвективного теплообмена, имеющую единственное решение.
3.3.Приближение Буссинеска
взадачах свободной тепловой конвекции
Свободная конвекция жидкости определяется разностью плотностей холодных и нагретых ее слоев. Уравнение Навье – Стокса в форме (3.22) получено без учета зависимости физических свойств жидкости от температуры, в частности, в нем не учтена зависимость плотности от температуры.
Рассмотрим на примере уравнения Навье – Стокса приближенный способ учета переменной плотности в неоднородном температурном поле, называемый приближением Буссинеска:
|
du |
|
|
∂ p |
∂ |
2u |
|
|
|||
ρ |
|
= ρ |
g− |
|
+ µ |
|
|
|
. |
(3.34) |
|
dτ |
∂ |
∂ |
y2 |
||||||||
|
|
|
x |
|
|
||||||
92
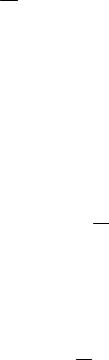
Входящая в это уравнение плотность принимается в соответствии с уравнением состояния линейно зависящей от температуры:
ρ = ρ 0 |
1 − β (T − T0 ) = ρ |
0 (1 − β ∆ T ) , |
(3.35) |
|
|
|
|
|
|
где β, [1/К] – коэффициент теплового (объемного) расширения. После подстановки зависимости (3.35) в уравнение (3.34) получаем:
|
|
|
|
du |
|
∂ p |
∂ |
2u |
|
|
||
ρ |
|
(1− β∆ |
T ) |
= |
ρ |
−(1β∆ |
T− ) g + µ |
|
|
|
. |
(3.36) |
|
∂ |
y2 |
||||||||||
|
0 |
|
|
dτ |
0 |
∂ x |
|
|
||||
Так как ускорение свободного падения значительно больше ускорения частиц жидкости при свободной конвекции ( g >> du dτ ), то изменением плотности в левой части уравне-
dτ ), то изменением плотности в левой части уравне-
ния (3.36) можно пренебречь по сравнению с изменением ее в правой части уравнения, в результате получаем:
|
|
du |
|
|
(−1 |
β∆ T −) g |
∂ p |
|
∂ 2u |
|
|||||
ρ |
0 |
|
|
= ρ |
0 |
+ µ |
|
|
|
|
|
||||
dτ |
|
∂ |
y2 |
|
|||||||||||
|
|
|
|
|
∂ x |
|
|
||||||||
или после деления на плотность ρ0: |
|
|
|
|
|
|
|
||||||||
|
du |
= (1 |
|
|
T ) g− |
1 |
∂ p |
∂ |
2u |
|
|
||||
|
|
|
− β∆ |
|
+ |
ν |
|
|
|
. |
(3.37) |
||||
|
dτ |
|
∂ |
|
|||||||||||
|
|
|
|
|
|
ρ 0 ∂ x |
y2 |
|
|
||||||
Полученное одномерное уравнение описывает свободную тепловую конвекцию жидкости в приближении Буссинеска.
В общем трехмерном случае для вектора скорости W (u, v, w) уравнение движения в этом приближении принимает вид:
dW |
= (1 − β∆ T ) g− |
1 |
|
|
|
|
|
+pν |
2W . |
(3.38) |
|
dτ |
ρ 0 |
3.4.Постановка задачи тепловой конвекции
вдинамических переменных
Постановкой задачи называется система уравнений переноса, замкнутая условиями однозначности.
93
Постановку краевой задачи тепловой конвекции рассмотрим на примере плоского движения несжимаемой вязкой жидкости с постоянными свойствами в горизонтальном каннале прямоугольного сечения (рис. 3.11). Боковые стенки канала приняты изотермическими с температурами t1 и t2 (t1 > t2), верхняя и нижняя стенки – адиабатными. Вязкая среда, нагреваясь у левой стенки, поднимается вследствие уменьшения плотности вверх и опускается соответственно вниз при охлаждении у правой стенки. Образуется замкнутый контур циркуляции
Рис. 3.11. Расчетная схема |
жидкости с пограничными сло- |
|
ями у стенок канала. |
||
|
Запишем систему уравнений тепловой конвекции. Уравнение несжимаемости для компонент вектора скорости u и v соответственно в проекциях на оси x и y в плоскости циркуляции
жидкости принимает вид: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∂ u |
+∂ |
|
v |
= 0. |
(3.39) |
|||
|
|
|
|
|
|
y |
||||||
|
|
|
|
∂ x |
∂ |
|
|
|
||||
Уравнение переноса тепловой энергии: |
|
|||||||||||
|
∂ T |
+ u∂ |
T |
+ ν∂ |
|
T |
= a 2T , |
(3.40) |
||||
|
∂τ |
x |
|
|
||||||||
|
∂ |
|
|
∂ |
y |
|
||||||
где оператор Лапласа в правой части уравнения имеет вид:
2 |
∂ 2 |
∂ |
2 |
|
|
= |
+ |
∂ |
y2 |
. |
(3.41) |
|
∂ x2 |
|
|
Запишем уравнения движения вязкой среды в приближении Буссинеска соответственно в проекциях на оси x и y:
94

|
|
|
∂ u |
+ u∂ |
|
u |
+ ν∂ |
u |
= − |
1∂ |
|
p |
+ ν |
2u , |
(3.42) |
||||
|
|
|
|
|
|
|
|
|
∂ 0 |
|
|||||||||
|
|
|
∂τ |
∂ |
x ∂ |
y |
ρ |
|
x |
|
|
|
|
||||||
∂ v |
+ u∂ |
v |
+ ν∂ |
|
v |
= − |
g (1− β ∆ T )− |
|
1∂ |
p+ ν 2v . |
(3.43) |
||||||||
∂τ |
|
|
|
|
∂ 0 |
||||||||||||||
∂ |
x |
∂ |
y |
|
|
|
|
ρ |
|
y |
|
||||||||
Уравнение, описывающее распределение давления, можно получить, сложив уравнения движения (3.42) и (3.43), первое из которых предварительно продифференцировав по x, а второе – по y. После преобразований получим уравнение Пуассона для давления:
|
2 |
|
|
∂ T |
|
|
|
u ∂ |
|
v ∂ |
|
u∂ |
|
v |
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|||||||
|
|
p= ρ β 0 |
g |
− |
ρ 2 |
0 |
|
y ∂ |
− |
x |
∂ |
|
x∂ |
|
|
. |
(3.44) |
|
|
|
|
||||||||||||||
|
|
|
|
∂ y |
|
|
∂ |
|
|
|
y |
|
|||||
Для замыкания системы дифференциальных уравнений запишем краевые условия, включающие начальные температуру и поле скоростей, а также граничные температурные условия на изотермических и адиабатных границах и условия прилипания для скоростей:
|
T (τ = 0)= T0 , u (τ = 0)= v(τ = 0=) 0, |
|
|||||
|
|
||||||
T (0, |
y ) = T1 , T ( H x , y ) = T2 , |
∂ T |
( x, |
0) =∂ |
T |
(x, H y ) = 0, (3.45) |
|
|
|
||||||
|
|
∂ y |
∂ y |
|
|||
|
u (0, y ) = u ( H x , y ) = v( x, 0) = v(x, H y ) = 0. |
|
|||||
|
|
||||||
Пять дифференциальных уравнений (3.39, 3.40, 3.42, 3.43 и 3.44) вместе с краевыми условиями (3.45) образуют краевую задачу тепловой конвекции, граничные значения для давления в которой определяются приближенно из уравнения Пуассона (3.44). Переменные u–v–p– Т называют динамическими переменными, а соответствующую краевую задачу – задачей в ди-
намических переменных.
Таким образом, в динамических переменных плоская задача тепловой конвекции сводится к системе пяти дифференциальных уравнений с соответствующими краевыми условиями.
95

3.5. Постановка задачи тепловой конвекции в переменных завихренность-функция тока
Рассмотрим другую постановку этой же задачи, исключающую давление и уменьшающую тем самым число дифференциальных уравнений тепловой конвекции. Для этого вычтем из уравнения (3.42) уравнение (3.43), предварительно продифференцировав первое из них по y, а второе – по x. В результате получим:
∂ |
|
∂ u |
∂ |
u |
∂ |
|
|
|
|
|
+ u |
|
+ ν |
∂ |
|
|
x |
|||
y ∂τ |
∂ |
∂ |
||||
= ν ∂
∂ y
u |
|
∂ |
∂ |
v |
∂ |
|
|
− |
|
|
|
+ |
|
|
|
|
||||
y ∂ |
|
∂τx |
∂ |
|||
2−u |
|
∂ |
2+v |
β |
||
|
|
∂ |
x |
|
|
|
|
|
v∂ |
v |
|
|||
u |
|
|
+ ν |
|
= |
|
|
|
|
|
|
||||
|
|
x∂ |
|
|
|
|
|
|
|
|
|
y |
(3.46) |
||
|
∂ |
|
T |
|
|
|
|
g |
. |
|
|
|
|||
∂ |
|
|
|
|
|||
|
x |
|
|
|
|||
Кроме того, вводим функцию тока ψ, связанную с компонентами скорости соотношениями:
∂ ψ |
= u, − |
∂ψ |
|
= ν |
(3.47) |
∂ y |
|
∂ |
x |
|
|
и удовлетворяющую уравнению несжимаемости (3.39). По физическому смыслу функция тока характеризует объемный расход вязкой среды в единицу времени. Действительно, из первого уравнения (3.47) следует:
dψ = udy , ψ = ∫udy+ C, м2  с.
с.
Подставляя соотношения (3.47) в уравнение (3.46) и обозначая
∂ν |
∂ |
|
|
u ∂ ψ |
2 ∂ ψ |
2 |
= − |
2 |
ψ = ω , |
|
|||
|
− |
|
|
|
= |
|
|
+ |
|
|
(3.48) |
||
∂ |
∂ |
|
|
|
y2 |
|
|||||||
x |
y ∂ |
x2 ∂ |
|
|
|
|
|||||||
где ω – завихренность, получим уравнение переноса завихренности
∂ω |
∂ω |
|
∂ω |
2 |
∂ |
T |
|
||
∂τ |
+ u∂ |
|
+ ν∂ |
|
= ν ω + |
β g∂ |
|
. |
(3.49) |
x |
y |
x |
|||||||
96
Сравнение полученного уравнения с уравнениями переноса энергии и движения (переноса импульса) позволяет сделать вывод о том, что эти уравнения совпадают по своей структуре. Следовательно, перенос завихренности подчиняется тем же законам переноса, что и энергии и импульс.
Таким образом, формулировка задачи тепловой конвекции в ω– ψ– t-переменных приводит к системе трех дифференциальных уравнений: переноса энергии (3.40), переноса завихренности (3.49) и Пуассона (3.48), в которых скорость связана с функцией тока соотношениями (3.47).
Начальные краевые условия для завихренности и функции тока имеют вид:
ω τ( = 0=) 0 , ψ (τ = 0)= 0 .
Граничные значения функции тока следуют из отсутствия расхода вязкой среды через непроницаемые стенки канала. Функция тока на стенках канала не должна изменяться, следовательно, она должна быть постоянной, или, в частности, нулевой:
ψ (0, y ) = ψ ( H x , y ) = ψ ( x, 0) = ψ (x, H y ) = 0 .
Граничные значения завихренности определяются приближенно из уравнения Пуассона (3.48).
Формулировка плоской задачи тепловой конвекции несжимаемой жидкости в (ω– ψ– Т) переменных оказывается предпочтительнее формулировки ее в динамических (u–v–p– Т) переменных, так как понижает порядок системы дифференциальных уравнений с пяти до трех.
3.6. Постановка краевой задачи теплопроводности
Краевая задача теплопроводности включает дифференциальное уравнение теплопроводности, имеющее единственное решение при заданном начальном распределении температуры и условиях теплообмена на границах расчетной области.
97

Дифференциальное уравнение теплопроводности
Дифференциальное уравнение теплопроводности является частным случаем уравнения переноса энергии и связывает производные температуры по координате и времени:
∂ T |
= a 2T+ |
qV |
. |
(3.50) |
∂τ |
|
|||
|
ρ c |
|
||
Физический смысл уравнения: тепло от внутренних ис-
точников заданной мощности qV, а также тепло, подведенное к элементарному объему от соседних теплопроводностью a 2T , идет на увеличение внутренней энергии этого элементарного объема ∂ T ∂τ .
Коэффициент пропорциональности а называется коэффи-
циентом температуропроводности:
a = |
λ |
|
Вт м |
3 |
|
кг К |
|
м |
2 |
|
|
|||
|
|
|
|
. |
(3.51) |
|||||||||
|
|
|
|
|
|
|
|
|
||||||
ρ c |
м К кг Дж |
с |
||||||||||||
|
|
|
|
|
||||||||||
Он характеризует скорость изменения температуры и яв-
ляется мерой теплоинерционных свойств тела. При прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности.
Частные случаи уравнения теплопроводности:
1) qV =0 |
∂ T |
= a 2T |
– уравнение Фурье, описывает не- |
|
∂τ |
||||
|
|
|
стационарную теплопроводность в теле без источников (стоков) тепла;
|
0 |
2 |
qV |
|
уравнение Пуассона, опи- |
2) ∂ T ∂τ = |
T+ |
λ |
= 0 – |
сывает стационарную теплопроводность в теле с источниками (стоками) тепла;
3) qV =0, ∂ T ∂τ = 0 2T= 0 – уравнение Лапласа, опи-
сывает стационарную теплопроводность в теле без источников (стоков) тепла.
98
Уравнение теплопроводности при неоднородных свойствах
Дифференциальное уравнение теплопроводности (3.50) было получено в предположении постоянной теплопроводности (λ = const), в действительности теплопроводность зависит от температуры, λ = λ(Т), поэтому при выводе уравнения теплопроводности нельзя выносить плотность теплового потока за знак дивергенции. В этом случае уравнение теплопроводности становится нелинейным, так как входящий в него коэффициент λ зависит от распределения температуры:
ρ c |
∂ T |
= λ( +T ) qV . |
(3.52) |
|
|||
|
∂τ |
|
|
Нелинейное уравнение теплопроводности (3.52) можно привести формально к виду линейного уравнения (3.50), для этого преобразуем диффузионный член уравнения:
λ( |
2 |
Tλ + |
2 |
|
λ |
|
|
T |
2 |
T |
|
T= )λ + λT = |
|
T |
= λ |
2 |
|
|
эфф |
||||
|
|
|
|
|
|
|
T |
|
|
|
|
С введением понятий эффективных коэффициентов теплопроводности
λ эфф= λ + |
λ |
T |
(3.53) |
|
2T |
и температуропроводности
aэфф = |
λ эфф |
|
(3.54) |
|
ρ (T ) c |
(T ) |
|||
|
|
дифференциальное уравнение теплопроводности принимает стандартный вид:
∂ T |
= a |
эфф |
2T+ |
qV |
, |
(3.55) |
|
ρ c |
|||||
∂τ |
|
|
|
|||
|
|
|
|
|||
удобный при численной реализации на компьютере.
99
Уравнение теплопроводности для анизотропных сред
Анизотропной называется среда, в которой значение величины, определяющей свойства (в частности, теплопроводность), зависит от направления.
В общем случае закон Фурье можно записать в тензорном виде:
qi = −λ i, j
Тензор теплопроводности λ i, динат имеет следующий вид:
|
|
|
λ |
λ |
|
|
|
i, j |
= λ |
|
|
|
|
|
|
|
|
|
λ |
|
|
|
jT , i = x, y, z.
j в прямоугольной системе коор-
xx |
λ |
xy |
λ |
xz |
|
yx λ |
|
yy λ |
|
|
|
|
|
yz . |
|||
|
λ |
|
λ |
|
|
zx |
zy |
zz |
|||
Выбором системы координат тензор теплопроводности можно привести к виду:
|
λ |
xx |
0 |
0 |
|
|
λ i, j = |
|
0 |
λ yy |
0 |
|
, |
|
|
|||||
|
|
|
0 |
|
|
|
|
0 |
λ zz |
|
|||
уравнение теплопроводности имеет вид:
|
∂ T |
|
|
|
∂ |
T |
+∂ |
|
|
∂ |
T |
|
|
λ ∂ |
T+ |
|
|
||
ρ c |
= ∂ |
λ |
|
λ |
+∂ |
|
q |
|
|||||||||||
|
|
xx |
|
|
yy |
|
|
||||||||||||
|
∂τ ∂ |
|
|
|
∂ |
|
|
|
|
|
|
zz |
|
V |
|
||||
|
x |
|
∂ |
x |
y |
∂ |
y ∂ |
z ∂ |
|
z |
|
|
|||||||
|
∂ T |
|
λ xx |
|
2 |
|
|
|
λ |
yy∂ |
|
= |
∂ |
T |
+ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
∂τ |
|
|
∂ x |
2 |
λ xx∂ |
|||||
|
|
ρ c |
|
|
|||||||
С учетом обозначений
2T +
y2 λ
axx
λ zz∂
∂xx
= λ
2T + ρqV . z2 c
xx 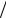 (ρ c), ky = λ yy λ xx ,
(ρ c), ky = λ yy λ xx ,
kz = λ zz λ xx уравнение теплопроводности принимает стандартный вид:
100
