
hfhf
.docx
Кинематикой называется раздел механики, в котором изучается движение тел без учета взаимодействий между ними, т.е. без выяснения причин, вызываю-щих или изменяющих состояние движения.
Совокупность тела отсчета, связанной с ним системы координат и часов образуют систему отсчета.
Линия, вдоль которой материальная точка движется в пространстве в данной системе отсчета, называется траекторией движения.
Вектор, проведенный из начального положения материальной точки в положе-ние, где точка находится в рассматриваемый момент времени, называется векто-ром перемещения . Δr
Путь представляет собой длину участка траектории , пройденного точкой за некоторый промежуток времени. S
Если движение равномерное (), при получим . Если движение равнопеременное (), при имеем: ()consttυ=00=t ()tSυ=consta=00t=
|
|
|
||
|
1. Кинематика материальной точки. Система отсчета. Траектория, перемещение, скорость, ускорение. Равномерное и равнопеременное прямолинейное движение. 2. Криволинейное движение. Нормальное и тангенсальное ускорения. 3. Движение точки по окружности. Угловые перемещение, ускорение, скорость. Связь между линейными и угловыми характеристиками. 4. Динамика материальной точки. Инерциальные системы отсчета и первый закон Ньютона. 5. Фундаментальные взаимодействия. Силы различной природы(упругие, гравитационные, трения). Второй закон Ньютона. Масса. Третий закон Ньютона. 6. Импульс системы материальных точек. Уравнение движения центра масс. Закон сохранения импульса. 7. Уравнение движения тела переменной массы ( уравнение Мещерского). 8. Момент импульса и момент силы. Уравнение моментов. Закон сохранения момента импульса. Гироскопические явления. 9. Вращение твердого тела вокруг неподвижной оси. Основной закон динамики вращательного движения абсолютно твердого тела. Момент инерции. 10. Расчет момента инерции тел простой формы. Теорема Штейнера. 11. Кинетическая энергия материальной точки и абсолютно твердого тела. 12. Работа переменной силы, мощность. Потенциальные и непотенциальные поля. Консервативные и диссипативные силы. Потенциальная энергия. 13. Закон всемирного тяготения. Поле тяготения, его напряженность и потенциальная энергия гравитационного взаимодействия. 14. Работа по перемещения тела в поле тяготения. Космические скорости. 15. Соударения тел. Упругое и неупругое взаимодействия. 16. Колебательное движение и его характеристики: смещение, амплитуда, фаза, циклическая частота, период, скорость, ускорение. 17. Векторные диаграммы для представления гармонических колебаний. Дифференциальное уравнение гармонических колебаний. Энергия колебательного движения. 18. Пружинный и физический маятники. 19. Сложение параллельных колебаний одинаковой и разной частоты. Биения. Сложения колебаний одинаковой частоты Сложение колебаний разной частоты 20. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. 21. Свободные затухающие колебания. Характеристики затухания: коэффициент затухания, время релаксации, декремент затухания, добротность колебательной системы. 22 Вынужденные колебания. Резонанс. 24. Термодинамическая система параметры состояния термодинамической системы. Основные положения молекулярно-кинетической теории газов. 25. Закон равномерного распределения энергии по степеням свободы молекул. Основное уравнение молекулярно-кинетической теории газов. 26. Закон Максвелла распределения молекул по скоростям теплового движения. Барометрическая формула. Распределение Больцмана. 27. Среднее число столкновений и средняя длина свободного движения молекул. 28. Первый закон термодинамики. Работа, теплота, теплоемкость, ее виды. 29. Политропный процесс, его частные случаи: изобарный, изотермический, адиабатный, изохорный. 30. Второй закон термодинамики. Энтропия. Тепловые двигатели и холодильные машины. Цикл Карно. 1 Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение. Система отсчета – тело отсчета, система координат, связанная с ним, и прибор для измерения времени. Перемещение – направленный отрезок (вектор) между начальным и конечным положением тела. ^ Траектория (l) – линия, вдоль которой движется тело. Путь (S) – длина траектории. Скорость (V) – величина, показывающая какой путь проходит тело за единицу времени.
Ускорение
– это величина, показывающая, как
изменяется скорость за одну секунду.
^
Равномерное прямолинейное
движение
Равномерным
прямолинейным движением называется
такое прямолинейное движение, при
котором материальная точка (тело)
движется по прямой и в любые равные
промежутки времени совершает одинаковые
перемещения.
уравнение равномерного
движения:
Sx = Vx · t. Координата
тела в начальный момент t = 0.
^
Равнопеременное прямолинейное
движение
Равнопеременным
называется движение, при котором
скорость тела (материальной точки) за
любые равные промежутки времени
изменяется одинаково, т.е. на равные
величины. Это движение может быть
равноускоренным и равнозамедленным.
Так
как координата тела равна х = х0
+ S, то уравнение движения тела имеет
вид:
Криволинейные
движения
– движения, траектории которых
представляют собой не прямые, а кривые
линии. По криволинейным траекториям
движутся планеты, воды рек.
В
случае криволинейного движения с
постоянным ускорением в плоскости
XOY проекции vx и vy ее скорости на оси Ox
и Oy и координаты x и y точки в любой
момент времени t определяется по
формулам:
Движение
по окружности всегда есть движение
ускоренное: модуль скорости все время
направлен по касательной к траектории,
постоянно меняет направление, движение
по окружности всегда происходит с
центростремительным ускорением.
^
Связь между линейными и угловыми
величинами, характеризующими движение
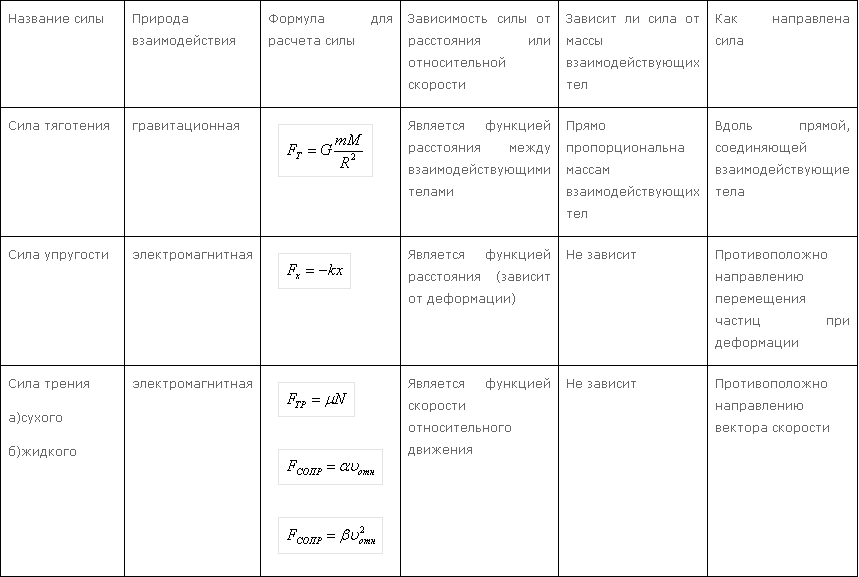
Динамика изучает движение тела в связи с теми причинами (взаимодействиями между телами), которые обуславливают тот или иной характер движения. Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. F=0 Система отсчета, в которой выполняется первый закон Ньютона, называется инерциальной 5 Фундамента́льные взаимоде́йствия — различные, не сводящиеся друг к другу типы взаимодействия элементарных частиц и составленных из них тел. Четыре фундаментальных взаимодействия: гравитационное, электромагнитное, сильного и слабого взаимодействий. В
таблице переписать первые три
столбика!!!!!
6
Импульсом,
или количеством движения материальной
точки называется векторная величина,
равная произведению массы материальной
точки m на скорость ее движения
v.
Импульс системы материальных точек
(вычисляется через импульсы этих
точек)
Уравнение
движения центра масс:
^ Динамические характеристики вращательного движения: Момент инерции материальной точки равен
Моментом силы относительно оси вращения называют векторное произведение радиуса-вектора точки i на силу:
ТЕОРЕМА
ШТЕЙНЕРА
Переписать 1,2,3 столбик!!!!
Основное уравнение динамики вращательного движения:Переписать последнюю формулу 5.36!!!!
закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. В замкнутой системе момент внешних сил
Работа постоянной
силы, действующей на прямолинейно
движущееся тело
Мощность
потенциальными(консервативными) силами называются такие силы, работа которых зависит только от начальных и конечных положений точек их приложения и не зависит ни от вида траекторий этих точек, ни от законов их движения по траекториям Диссипативными силами называются силы, суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна 9 Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело. m1v1+m2v2=(m1+m2)V V=(m1v1+m2v2)/(m1+m2) Кин. энергии системы до удара и после: K1=1/2(m1v12+m2v22) K2=1/2(m1+m2)V Пользуясь этими выраж. получаем: K1-K2v=1/21v2v1-v2) где =m1m2/(m1+m2) приведенная масса шаров. Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кин. энергии макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости. ^ Абсолютно упругим ударом называется столкновение тел, в результате которого их внутренние энергии не меняются. Пример: Столкновение бильярдных шаров из слоновой кости, при столкновениях атомных, ядерных частиц. Рассмотрим центральный удар двух шаров, движущ-ся навстречу друг другу: (m1v12)/2+(m2 v22)/2=(m1u12)/2+(m2 u22)/2 и: m1v1+m2v2=m1u1+m2u2 u1=[(m1-m2)v1+2m2v2]/(m1 +m2) u2=[(m2-m1)v2+2m1v1]/(m1+m2) При столкновении двух одинаковых абсолютно упругих шаров они просто обмениваются скоростями. ^ 16. Колебательное движение и его характеристики: смещение, амплитуда, фаза, циклическая частота, период, скорость, ускорение. Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. ^ Классификации колебаний Выделение разных видов колебаний зависит от свойства, которое хотят подчеркнуть. Для подчёркивания разной физической природы колеблющихся систем выделяют, например, колебания:
По характеру взаимодействия с окружающей средой:
^ Характеристики колебательного движения: Смещение х - отклонение колеблющейся точки от положения равновесия в данный момент времени (м). Амплитуда А – максимальное отклонение тела от положения равновесия. Если колебания незатухающие, то амплитуда постоянна (м). Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с). ^ Фаза колебания - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад). Фаза колебания в начальный момент времени (t=0) называется начальной фазой. Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц) ^ Циклическая частота колебаний ω – это число полных колебаний, происходящих за 2π секунд. Единица циклической частоты – радиан в секунду (рад/с). ^ Скорость и ускорение при гармонических колебаниях. Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Согласно определению скорости, скорость – это производная от координаты по времени. Согласно определению ускорения, ускорение – это производная от скорости по времени: 17. Векторные диаграммы для представления гармонических колебаний. Дифференциальное уравнение гармонических колебаний. Энергия колебательного движения.
Векторные
диаграммы для представления гармонических
колебаний.
Колебаниями
называются движения или процессы,
которые характеризуются определенной
повторяемостью во времени.
^
Гармонические колебания
- колебания, при которых колеблющаяся
величина изменятся со временем по
закону синуса (косинуса).
Гармонические
колебания описываются уравнением
типа:
x
=A
cos (0
t
+)
,
где
x – смещение колеблющейся
точки от положения равновесия.
А
- максимальное значение колеблющейся
величины, называемое амплитудой
колебания,
0
- круговая
(циклическая) частота,
-
начальная фаза колебания
в момент времени t=0,
(0
t +)
- фаза
колебания
в момент времени t.
Гармонические
колебания изображаются графически
методом
вращающегося вектора амплитуды,
или методом
векторных диаграмм.
Для этого из произвольной точки
О, выбранной на оси x
под углом ,
равным начальной фазе колебания,
откладывается вектор А, модуль которого
равен амплитуде А
рассматриваемого
колебания.
18. Пружинный и физический маятники.
Пружинный
маятник
Колебательная
система в этом случае представляет
собой совокупность некоторого тела
и прикрепленной к нему пружины. Пружина
может располагаться либо вертикально
(вертикальный пружинный маятник), либо
горизонтально (горизонтальный пружинный
маятник).
19. Сложение параллельных колебаний одинаковой и разной частоты. Биения. |
|
^ Сложения колебаний одинаковой частоты векторная диаграмма сложения колебаний: 1) 2) Сложение колебаний разной частоты
Бие́ния
— явление, возникающее при наложении
двух гармонических колебаний близкой
частоты и выражающееся в периодическом
уменьшении и увеличении амплитуды
суммарного сигнала. Частота изменения
амплитуды суммарного сигнала равна
разности частот двух исходных
сигналов.
Биения возникают от
того, что один из двух сигналов постоянно
отстаёт от другого по фазе и в те
моменты, когда колебания происходят
синфазно, суммарный сигнал оказывается
усилен, а в те моменты, когда два сигнала
оказываются в противофазе, они взаимно
гасят друг друга. Эти моменты периодически
сменяют друг друга по мере того как
нарастает отставание.
20. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.
1)
w1=w2
1’)
2’)
3’)
При A1=A2
окружность
^
Фигу́ры Лиссажу́
— замкнутые траектории, прочерчиваемые
точкой, совершающей одновременно два
гармонических колебания в двух взаимно
перпендикулярных направлениях. Впервые
изучены французским учёным Ж. Лиссажу
(J. Lissajous; 1822—80). Вид фигур зависит от
соотношения между периодами (частотами),
фазами и амплитудами обоих колебаний.
В простейшем случае равенства обоих
периодов фигуры представляют собой
эллипсы, которые при разности фаз 0
или π вырождаются в отрезки прямых, а
при разности фаз π/2 и равенстве амплитуд
превращаются в окружность. Если периоды
обоих колебаний неточно совпадают,
то разность фаз всё время меняется,
вследствие чего эллипс всё время
деформируется. При существенно
различных периодах фигуры Лиссажу не
наблюдаются. Однако, если периоды
относятся как целые числа, то через
промежуток времени, равный наименьшему
кратному обоих периодов, движущаяся
точка снова возвращается в то же
положение — получаются фигуры Лиссажу
более сложной формы. Фигуры Лиссажу
вписываются в прямоугольник, центр
которого совпадает с началом координат,
а стороны параллельны осям координат
и расположены по обе стороны от них
на расстояниях, равных амплитудам
колебаний.
^ 21. Свободные затухающие колебания. Характеристики затухания: коэффициент затухания, время релаксации, декремент затухания, добротность колебательной системы.
Затуханием
колебаний
называется постепенное ослабление
колебаний с течением времени,
обусловленное потерей энергии
колебательной системой. Закон затухания
колебаний зависит от свойств
колебательной системы. Система
называется линейной, если параметры,
характеризующие существенные в
рассматриваемом процессе физические
свойства системы, не изменяются в ходе
процесса. Свободные затухающие
колебания линейной системы описываются
уравнением:
22 Вынужденные колебания. Резонанс.
Колебания,
происходящие под действием внешней
периодической силы, называются
вынужденными
колебаниями.
Внешняя периодическая сила, называемая
вынуждающей, сообщает колебательной
системе дополнительную энергию,
которая идет на восполнение энергетических
потерь, происходящих из-за трения.
Если вынуждающая сила изменяется во
времени по закону синуса или косинуса,
то вынужденные колебания будут
гармоническими и незатухающими.
В
отличие от свободных колебаний, когда
система получает энергию лишь один
раз (при выведении системы из состояния
равновесия), в случае вынужденных
колебаний система поглощает эту
энергию от источника внешней
периодической силы непрерывно. Эта
энергия восполняет потери, расходуемые
на преодоление трения, и потому
полная энергия колебательной системы
no-прежнему остается неизменной.
Частота
вынужденных колебаний равна частоте
вынуждающей силы.
В случае, когда частота вынуждающей
силы υ
совпадает с собственной частотой
колебательной системы υ0,
происходит резкое возрастание
амплитуды вынужденных колебаний —
резонанс.
Резонанс возникает из-за того, что при
υ
= υ0
внешняя
сила, действуя в такт со свободными
колебаниями, все время сонаправлена
со скоростью колеблющегося тела и
совершает положительную работу:
энергия колеблющегося тела
увеличивается, и амплитуда его колебаний
становится большой. График зависимости
амплитуды вынужденных колебаний Ат
от частоты вынуждающей силы υ
представлен
на рисунке, этот график называется
резонансной кривой:
24. Термодинамическая система параметры состояния термодинамической системы. Основные положения молекулярно-кинетической теории газов. Термодинамическая система — это любая область пространства, ограниченная действительными или воображаемыми границами, выбранными для анализа её внутренних термодинамических параметров. Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества. Границы термодинамической системы могут быть неподвижными или подвижными. Системы могут быть большими или маленькими, в зависимости от границ. Система может существовать в вакууме или может содержать несколько фаз одного или более веществ. Термодинамические системы могут содержать сухой воздух и водяной пар (два вещества) или воду и водяной пар (две стадии одного и того же вещества). Однородная система состоит из одного вещества, одной его фазы или однородной смеси нескольких компонентов. Системы бывают изолированными (замкнутыми) или открытыми. В изолированной системе не происходит никаких обменных процессов с внешней средой. В открытой системе и энергия и вещество могут переходить из системы в среду и обратно. ^ Состояние термодинамической системы определяется физическими свойствами вещества. Температура, давление, объем, внутренняя энергия, энтальпия и энтропия — это термодинамические величины, определяющие те или иные интегральные параметры системы. Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия. Различают экстенсивные параметры состояния, пропорциональные массе термодинамической системы, и интенсивные параметры состояния, не зависящие от массы системы. К экстенсивным параметрам состояния. относятся: объём, Внутренняя энергия, Энтропия, Энтальпия, изохорно-изотермический потенциал Гиббсова энергия), изобарно-изометрический потенциал (Гельмгольцева энергия); к интенсивным параметрам состояния— давление, температура, концентрация, магнитная индукция и др. параметры состояния взаимосвязаны, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния. В молекулярно-кинетической теории поль зуются идеализированной моделью идеаль ного газа, согласно которой: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсутству ют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие. Модель идеального газа можно ис пользовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. ^ 25. Закон равномерного распределения энергии по степеням свободы молекул. Основное уравнение молекулярно-кинетической теории газов.
Число
степеней свободы – это число независимых
величин с помощью которых может быть
задано положение системы. (1 атом =3
ст., 2 атома =5ст. 3 атома=6ст.)
^
Закон Больцмана о равномерном
распределении энергии по степеням
свободы молекул:
для статической системы, находящейся
в состоянии термодинамического
равновесия, на каждую поступательную
и вращательную степени свободы
приходится в среднем кинетическая
энергия, равная КТ/2 , а на каждую
колебательную – КТ
средняя
энергия приходящаяся на одну степень
свободы:
26. Закон Максвелла распределения молекул по скоростям теплового движения. Барометрическая формула. Распределение Больцмана.
Закон
Максвелла распределения молекул по
скоростям теплового движения
Закон
Максвелла описывается некоторой
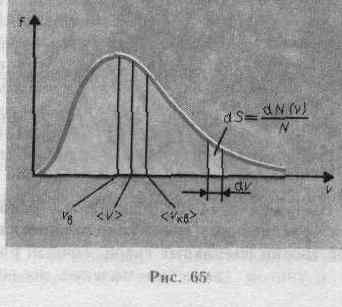
функцией f(v), называемой функцией
распределения молекул по скоростям.
Если разбить диапазон скоростей
молекул на
малые интервалы, равные
dv, то на каждый интервал скорости будет
приходиться некоторое число молекул
dN(v), имеющих скорость, заключенную в
этом интервале. Функция f(v) определяет
относительное число молекул dN (v)/N,
скорости которых лежат в интервале
от v до v+dv, т. е.
откуда
f(v)=dN(v)/Ndv.
Применяя методы теории
вероятностей, Максвелл нашел функцию
f(v) — закон
для распределения молекул идеального
газа по скоростям:
27. Среднее число столкновений и средняя длина свободного движения молекул.
Молекулы
газа, находясь в состоянии хао тического
движения, непрерывно сталки ваются
друг с другом. Между двумя по
следовательными столкновениями молеку
лы проходят некоторый путь l,
который называется длиной
свободного пробега. В
общем случае длина пути между по
следовательными столкновениями различ
на, но так как мы имеем дело с огромным
числом молекул и они находятся в бес
порядочном движении, то можно говорить
о средней
длине свободного пробега моле кул
<l>.
Минимальное
расстояние, на которое сближаются при
столкновении центры двух молекул,
называется эффективным
диаметром молекулы d
(рис.68).
Он за висит от скорости сталкивающихся
моле кул, т. е. от температуры газа
(несколько уменьшается с ростом
температуры).
Так как за 1 с молекула
проходит в среднем путь, равный средней
арифметической скорости , и если (z)
—сред нее число столкновений,
испытываемых одной молекулой газа за
1 с, то средняя длина свободного
пробега
28. Первый закон термодинамики. Работа, теплота, теплоемкость, ее виды.
Допустим,
что некоторая система (газ, заключенный
в цилиндр под поршнем), обладая
внутренней энергией U1,
получи
ла некоторое количество теплоты Q и,
перейдя в новое состояние, характеризую
щееся внутренней энергией U2,
совершила
работу А
над
внешней средой, т. е. против внешних
сил. Количество теплоты считает ся
положительным, когда оно подводится
к системе, а работа — положительной,
когда система совершает ее против
внеш них сил. Опыт показывает, что в
соответ ствии с законом сохранения
энергии при любом способе перехода
системы из перво го состояния во второе
изменение внутрен ней энергии U=U2-U1
будет одинако вым и равным разности
между количест вом теплоты Q, полученным
системой, и работой А,
совершенной
системой про тив внешних
сил:
U=Q-A,
или
Q=U+A.
(51.1)
Уравнение
(51.1) выражает первое
начало термодинамики:
теплота, сообщаемая системе, расходуется
на изменение ее внутренней энергии и
на совершение ею работы против внешних
сил.
Выражение (51.1) в дифференциаль
ной форме будет иметь вид
dQ=dU+dA,
где
dU — бесконечно малое изменение
внутренней энергии системы.
Работа
Для
рассмотрения конкретных процессов
найдем в общем виде внешнюю работу,
совершаемую газом при изменении его
объема. Рассмотрим, например, газ, на
ходящийся под поршнем в цилиндриче
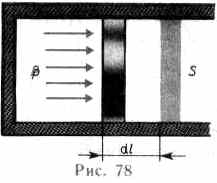
ском сосуде (рис. 78). Если газ, расширя
ясь, передвигает поршень на бесконечно
малое расстояние dl,
то производит над ним
работу
A=Fdl=pSdl=pdV,
где
S — площадь поршня, Sdl=dV—
из менение объема системы. Таким
образом,
^
A=pdV. (52.1)
Полную
работу A, совершаемую газом при изменении
его объема от V1
до V2,
найдем
29. Политропный процесс, его частные случаи: изобарный, изотермический, адиабатный, изохорный.
Процесс,
в ко тором теплоемкость остается
постоянной, называется политропным.
Исходя
из первого начала термодина мики при
условии постоянства теплоемко сти (C
= const) можно вывести уравнение
политропы:
pVn
= const,
(55.9) где n=(C-Ср)/(С-Cv)
—
показатель политропы. Очевидно, что
при С = 0, n=
из (55.9) получается уравнение адиабаты;
при С=,
n =1 —уравнение изотермы; при С=СР,
n = 0
— уравнение
изобары, при С
= Сv,
n=±
—уравнение изохоры.
Среди
равновесных процессов, происходя щих
с термодинамическими системами,
выделяются изопроцессы,
при
которых один из основных параметров
состояния сохраняется постоянным.
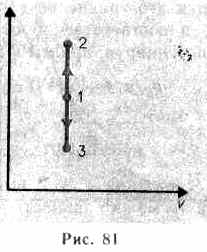
Изохорный
процесс
(V = const). Диаг рамма этого процесса
(изохора)
в
коорди натах р,
V изображается
прямой, парал лельной оси ординат
(рис. 81), где процесс 1—2
есть
изохорное нагревание, а 1—3
— изохорное
охлаждение. При изохорном процессе
газ не совершает работы над внешними
телами, т. е.
A=pdV
= 0.
Как
уже указывалось в § 53, из первого начала
термодинамики Q=dU(+A)
для изохорного процесса следует, что
вся теп лота, сообщаемая газу, идет на
увеличе ние его внутренней энергии:
Q
=dU
Согласно
формуле (53.4), dUm
= CvdT.
Тогда
для произвольной массы газа по
лучим
30. Второй закон термодинамики. Энтропия. Тепловые двигатели и холодильные машины. Цикл Карно.
Второе
начало термодинамики
можно сформулиро вать как закон
возрастания энтропии зам
кнутой системы при необратимых процес
сах: любой необратимый процесс в замкну
той системе происходит так, что энтропия
системы при этом возрастает.
Можно
дать более краткую формули ровку
второго начала термодинамики: в
процессах, происходящих в замкнутой
системе, энтропия не убывает. Здесь
су щественно, что речь идет о замкнутых
системах, так как в незамкнутых системах
энтропия может вести себя любым обра
зом (убывать, возрастать, оставаться
по стоянной). Кроме того, отметим еще
раз, что энтропия остается постоянной
в за мкнутой системе только при
обратимых процессах. При необратимых
процессах в замкнутой системе энтропия
всегда воз растает.
Формула
Больцмана S = klnW, где k — постоянная
Больцмана, позволяет объяснить
постулируемое вторым началом
термодинамики возрастание энтропии
в замкнутой системе при необратимых
процессах: возрастание
энтропии означает
переход системы из
менее вероятных в бо лее вероятные
состояния.
Таким образом, формула Больцмана
позволяет дать стати стическое
толкование второго начала термодинамики.
Оно, являясь статистиче ским законом,
описывает закономерности хаотического
движения большого числа частиц,
составляющих замкнутую систе му.
^
Понятие энтропии
введено в 1865г. Р. Клаузиусом. Для
выяснения физическо го содержания
этого понятия рассматри вают отношение
теплоты Q,
полученной телом в изотермическом
процессе, к темпе ратуре Т
теплоотдающего
тела, называе мое приведенным
количеством теплоты.
Приведенное
количество теплоты, со общаемое телу
на бесконечно малом участке процесса,
равно ^
Q/T. Строгий
теоретический анализ показывает, что
приведенное количество теплоты, сообща
емое телу в
любом обратимом круговом процессе,
равно
нулю:
|

 ^
Второй закон Ньютона:
Если
на частицу с массой т окружающие тела
действуют с силой
^
Второй закон Ньютона:
Если
на частицу с массой т окружающие тела
действуют с силой
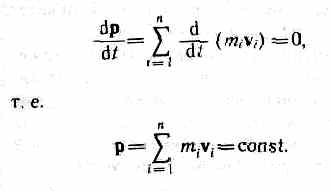 7
7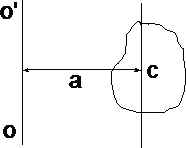 рис
6.
Момент инерции тела относительно
произвольной оси может быть рассчитан
по теореме Штейнера: момен
тинерции тела относительно оси O'O
равен сумме момента инерции тела
относительно оси, проходящей через
центр инерции и параллельной O'O, и
произведения массы тела на квадрат
расстояния между осями(рис. 6):
рис
6.
Момент инерции тела относительно
произвольной оси может быть рассчитан
по теореме Штейнера: момен
тинерции тела относительно оси O'O
равен сумме момента инерции тела
относительно оси, проходящей через
центр инерции и параллельной O'O, и
произведения массы тела на квадрат
расстояния между осями(рис. 6):

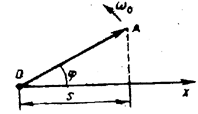 Если
этот вектор привести во вращение с
угловой скоростью 0,
равной циклической частоте колебаний,
то проекция конца вектора будет
перемещаться по оси x
и принимать значения от -А
до +А
,
а колеблющаяся величина будет изменяться
со временем по закону s =A
cos (0
t +).
Таким образом, гармоническое колебание
можно представить проекцией на
некоторую произвольно
выбранную ось вектора амплитуды А,
отложенного из произвольной точки
оси под углом ,
равным начальной фазе, и вращающегося
с угловой скоростью 0
вокруг этой точки.
^
Дифференциальное уравнение гармонических
колебаний материальной точки.
,
или , где m – масса точки, k – коэффициент
квазиупругой силы
(k=mw2).
Решение:
кинематическое
уравнение гармонических колебаний
Энергия
колебательного движения.
Если
этот вектор привести во вращение с
угловой скоростью 0,
равной циклической частоте колебаний,
то проекция конца вектора будет
перемещаться по оси x
и принимать значения от -А
до +А
,
а колеблющаяся величина будет изменяться
со временем по закону s =A
cos (0
t +).
Таким образом, гармоническое колебание
можно представить проекцией на
некоторую произвольно
выбранную ось вектора амплитуды А,
отложенного из произвольной точки
оси под углом ,
равным начальной фазе, и вращающегося
с угловой скоростью 0
вокруг этой точки.
^
Дифференциальное уравнение гармонических
колебаний материальной точки.
,
или , где m – масса точки, k – коэффициент
квазиупругой силы
(k=mw2).
Решение:
кинематическое
уравнение гармонических колебаний
Энергия
колебательного движения.
 Динамика
гармонических колебаний:
^
Динамика
гармонических колебаний:
^
 ^
^
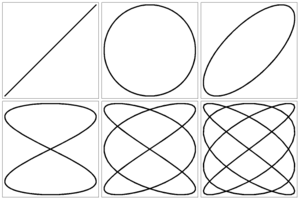
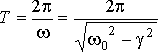 При
незначительном затухании период
колебаний практически равен
При
незначительном затухании период
колебаний практически равен
 Явление
резонанса играет большую роль в ряде
природных, научных и производственных
процессов. Например, необходимо
учитывать явление резонанса при
проектировании мостов, зданий и других
сооружений, испытывающих вибрацию
под нагрузкой, в противном случае при
определенных условиях эти сооружения
могут быть разрушены.
^
Явление
резонанса играет большую роль в ряде
природных, научных и производственных
процессов. Например, необходимо
учитывать явление резонанса при
проектировании мостов, зданий и других
сооружений, испытывающих вибрацию
под нагрузкой, в противном случае при
определенных условиях эти сооружения
могут быть разрушены.
^
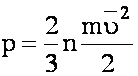 p
– давление газа, n - концентрация
молекул, m0
- масса молекулы.
^
p
– давление газа, n - концентрация
молекул, m0
- масса молекулы.
^
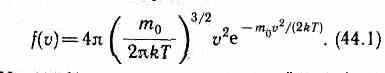 Из
(44.1) видно, что конкретный вид функции
зависит от рода газа (от массы молекулы)
и от параметра состояния (от температуры
Т).График функции (44.1) приведен на рис.
Так как при возрастании v множитель
уменьшается быстрее, чем растет
множитель v2, то функция f(v), начинаясь
от нуля, достигает максимума при vв
и затем асимптотически стремится к
нулю. Кривая несимметрична относительно
vв.
Из
(44.1) видно, что конкретный вид функции
зависит от рода газа (от массы молекулы)
и от параметра состояния (от температуры
Т).График функции (44.1) приведен на рис.
Так как при возрастании v множитель
уменьшается быстрее, чем растет
множитель v2, то функция f(v), начинаясь
от нуля, достигает максимума при vв
и затем асимптотически стремится к
нулю. Кривая несимметрична относительно
vв.
 ^
Барометрическая формула. Распределение
Больцмана
^
Барометрическая формула. Распределение
Больцмана
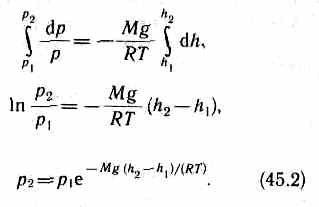 Выражение
(45.2) называется барометри
ческой формулой. Она
позволяет найти атмосферное давление
в зависимости от высоты или, измерив
давление, найти вы соту. Так как высоты
обозначаются отно сительно уровня
моря, где давление счита ется нормальным,
то выражение (45.2) может быть записано
в виде
Выражение
(45.2) называется барометри
ческой формулой. Она
позволяет найти атмосферное давление
в зависимости от высоты или, измерив
давление, найти вы соту. Так как высоты
обозначаются отно сительно уровня
моря, где давление счита ется нормальным,
то выражение (45.2) может быть записано
в виде
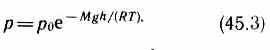 где
р
—
давление на высоте h.
Прибор для
определения высоты над земной
поверхностью называется высото
мером (или
альтиметром).
Его
работа ос нована на использовании
формулы (45.3). Из этой формулы следует,
что давление с высотой убывает тем
быстрее, чем тяже лее газ.
Барометрическую
формулу (45.3) можно преобразовать, если
воспользо ваться выражением (42.6)
p=nkT:
где
р
—
давление на высоте h.
Прибор для
определения высоты над земной
поверхностью называется высото
мером (или
альтиметром).
Его
работа ос нована на использовании
формулы (45.3). Из этой формулы следует,
что давление с высотой убывает тем
быстрее, чем тяже лее газ.
Барометрическую
формулу (45.3) можно преобразовать, если
воспользо ваться выражением (42.6)
p=nkT:
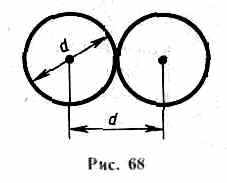 <l>=/.
Для
определения представим себе молекулу
в виде шарика диаметром d,
которая
движется среди других «застыв ших»
молекул. Эта молекула столкнется
только с теми молекулами, центры кото
рых находятся на расстояниях, рав ных
или меньших d,
т.
е. лежат внутри «ломаного» цилиндра
радиусом d.
Среднее
число столкновений за 1 с равно числу
молекул в объеме «ломано го»
цилиндра:
=nV,
где n
—
концентрация молекул, V = = d2
( —средняя скорость мо лекулы или
путь, пройденный ею за 1с). Таким образом,
среднее
число столкновений
d=n2.
Расчеты
показывают, что при учете дви жения
других молекул
<l>=/.
Для
определения представим себе молекулу
в виде шарика диаметром d,
которая
движется среди других «застыв ших»
молекул. Эта молекула столкнется
только с теми молекулами, центры кото
рых находятся на расстояниях, рав ных
или меньших d,
т.
е. лежат внутри «ломаного» цилиндра
радиусом d.
Среднее
число столкновений за 1 с равно числу
молекул в объеме «ломано го»
цилиндра:
=nV,
где n
—
концентрация молекул, V = = d2
( —средняя скорость мо лекулы или
путь, пройденный ею за 1с). Таким образом,
среднее
число столкновений
d=n2.
Расчеты
показывают, что при учете дви жения
других молекул
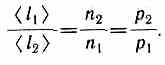 ^
^
 интегрированием
формулы (52.1):
интегрированием
формулы (52.1):
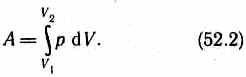 Результат
интегрирования определяется характером
зависимости между давлением и объемом
газа. Найденное для работы выражение
(52.2) справедливо при любых изменениях
объема твердых, жидких и га зообразных
тел.
Теплота
Теплота
- один из двух, известных современному
естествознанию, способов передачи
энергии - мера передачи неупорядоченного
движения. Количество переданной
энергии называют количеством
теплоты.
а) изохорный процесс
(V=const)
б) изобарный процесс
(p=const)
в) изотермическом
(T=const)
^
Теплоёмкость тела
(обозначается C) — физическая величина,
определяющая отношение бесконечно
малого количества теплоты ΔQ, полученного
телом, к соответствующему приращению
его температуры ΔT:
Результат
интегрирования определяется характером
зависимости между давлением и объемом
газа. Найденное для работы выражение
(52.2) справедливо при любых изменениях
объема твердых, жидких и га зообразных
тел.
Теплота
Теплота
- один из двух, известных современному
естествознанию, способов передачи
энергии - мера передачи неупорядоченного
движения. Количество переданной
энергии называют количеством
теплоты.
а) изохорный процесс
(V=const)
б) изобарный процесс
(p=const)
в) изотермическом
(T=const)
^
Теплоёмкость тела
(обозначается C) — физическая величина,
определяющая отношение бесконечно
малого количества теплоты ΔQ, полученного
телом, к соответствующему приращению
его температуры ΔT:
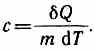 Единица
удельной теплоемкости — джоуль на
килограмм-кельвин (Дж/(кг•К)).
^
Молярная теплоемкость— величина,
равная количеству теплоты, необходимому
для нагревания 1 моля вещества на 1
К:
Единица
удельной теплоемкости — джоуль на
килограмм-кельвин (Дж/(кг•К)).
^
Молярная теплоемкость— величина,
равная количеству теплоты, необходимому
для нагревания 1 моля вещества на 1
К:
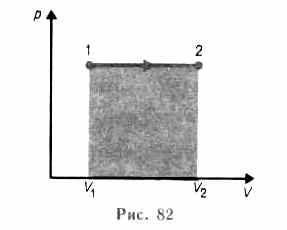 .
При изобарном процессе работа газа
при расширении объема от V1
до V2
равна
.
При изобарном процессе работа газа
при расширении объема от V1
до V2
равна
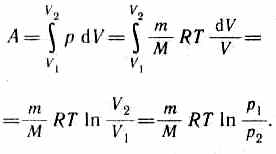 Так
как при T=const
внутренняя энергия идеального газа
не изменяется:
Так
как при T=const
внутренняя энергия идеального газа
не изменяется: