3.7. Магнитные свойства тела и вещества

Кривые намагничивания тела и вещества. Обычно требуется знать магнитные свойства ферромагнетиков как функции истинного, внутреннего магнитного поля. Однако на практике в большинстве случаев измеряется зависимость намагниченности от внешнего магнитного поля. Графический метод пересчета называется методом Релея (или методом сдвига).

Рис. 1.40. Построение кривой намагничивания материала (1)

по кривой намагничивания тела (2)

На рис. 1.40 кривая 2 соответствует кривой намагничивания тела. Для того чтобыпостроить кривую намагничивания вещества , необходимо знать размагничивающий фактор. Зная , можно построить зависимость намагниченности от размагничивающего поля, используя соотношения (1.107) и (1.108). Из них видно, что это прямая линия, наклон которой к оси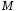определяется равенством

. (1.115)

Если провести прямую параллельно оси поля (,)_, то она пересечется с кривой в точке , соответствующей намагниченностии

внешнему полю , а с прямой в точке . Величина отрезка соответствует величине размагничивающего поля при намагниченности . Чтобы получить значение истинного поля при, отложим на прямой, параллельной оси, отрезок. Тогда величина отрезкадает значение внутреннего поля, соответствующее внешнему полю.

Таким способом можно определить для каждой точки кривой значение внутреннего поля и построить кривую намагниченности вещества (кривая 1 на рис. 1.40).

Такое же перестроение можно произвести для петли гистерезиса. При этом легко убедиться, что коэрцитивная сила остаётся неизменной для вещества и тела, а остаточная магнитная индукция для тела меньше, чем для вещества.

Можно также провести обратное построение и найти по кривой намагничивания материала кривую намагничивания тела с известным коэффициентом размагничивания, что используется при расчете различных магнитных устройств.

Магнитные свойства тела и вещества. Для истинной напряженности магнитного поля мы можем написать выражения:

(1.116)

, (1.117)

где и- восприимчивость и проницаемость материала (вещества).

Те же зависимости мы можем записать и для напряженности внешнего магнитного поля:

(1.118)

, (1.119)

где и, соответственно, восприимчивость и проницаемость тела.

Для одних и тех же значений намагниченности и индукции из выражений (1.116) и (1.118), а также выражений (1.117) и (1.119) следуют равенства

(1.120)

. (1.121)

Напряженности истинного и внешнего магнитных полей связаны выражениями:

(1.122)

или . (1.123)

Подставив выражение для из (1.122) в (1.120), а выражение (1.123) в (1.121), получим связь между восприимчивостями и проницаемостями тела и вещества:

, (1.124)

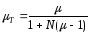. (1.125)

Аналогично, выразив из (1.122) и (1.123) 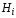и подставив его в (1.120) и (1.121), получим:

, (1.126)

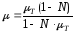. (1.127)

Из выражения (1.125) видно, что при проницаемость тела стремится к величине

, (1.128)

где - проницаемость формы, названная так потому, что зависит в основном от геометрических размеров. Аналогичный результат получается для восприимчивости. Значенияи могут быть измерены или рассчитаны.